-
Black hole physics has been one of the most important topics in physics during the last 50 years. Black hole thermodynamics is of special and fundamental importance, demonstrating that black holes are not merely mathematical singularities but rather should be considered as physical systems, with temperature and entropy [1]. Black hole thermodynamics combines the theories of classical thermodynamics, classical gravity, and quantum mechanics, paving a way to understand quantum gravity [2].
Recently, black hole thermodynamics in the so-called "extended phase space" has been garnering increasing attention [3]. In contrast to classical thermodynamics, there is no usual
$ p $ -$ V $ term in the first law of black hole thermodynamics. To restore this$ p $ -$ V $ term, the black hole phase space must be extended, so as to accommodate effective thermodynamic pressure and volume; thus, the theory bears its present name. In this framework, black hole thermodynamics is studied in the anti-de Sitter (AdS) space, with the cosmological constant$ \Lambda $ being negative. Moreover, if$ \Lambda $ is allowed to change, it plays the role of a positive varying pressure [4],$ p = - \frac{\Lambda}{8\pi} = \frac{3}{8\pi l^2}, $

(1) where
$ l $ is the AdS curvature radius. Furthermore, an effective thermodynamic volume$ V $ of a black hole can be introduced as the conjugate of$ p $ . Thus, the missing$ p $ -$ V $ term reappears in the first law of black hole thermodynamics. However, it is not the usual work term$ -p\, {{\rm{d}}} V $ but$ V\, {{\rm{d}}} p $ . Hence, the black hole mass should be identified as its enthalpy instead of internal energy, which distinctly characterizes the black hole thermodynamics in the extended phase space.In the extended phase space, AdS black holes exhibit strong similarities to non-ideal fluids [3]. For example, for the charged Reissner-Nordström-AdS (RN-AdS) black hole, there exists a large-small black hole transition, very much analogous to the gas–liquid phase transition of the van der Waals fluid. In addition, the critical exponents and equations of the corresponding states are exactly the same for these two seemingly unrelated systems. These remarkable observations have led to a large body of work, especially on phase transitions in various black hole solutions [5-40]. An excellent review of the recent progress in these areas can be found in Ref. [41].
One of the most interesting black hole phase transitions is the famous Hawking-Page (HP) phase transition [42], which was originally studied for the system of the Schwarzschild-AdS black hole and thermal AdS vacuum. In the AdS space, a large black hole (with a large horizon radius) has positive heat capacity and is thermodynamically stable; thus, it can be in an equilibrium with the thermal background. The partition function of the black hole-thermal AdS system is dominated by the black hole phase at high temperatures and by the thermal AdS phase in the limit of low temperatures. As a result, below a certain temperature (i.e., the HP temperature
$ T_{\rm{HP}} $ ), no black hole solutions exist anymore, while above$ T_{\rm{HP}} $ , the thermal AdS gas collapses into a stable large black hole. This phase transition was later widely studied in Refs. [43-56] and with an emphasis on the extended phase space in Refs. [57-61].The aim of this study is to investigate the HP phase transitions of charged AdS black holes surrounded by quintessence dark energy (hereafter, RN-qAdS black hole). In the last two decades, various cosmological observations have strongly suggested the accelerated expansion of our universe, which has been typically attributed to the existence of dark energy. One of the most promising dynamical candidates of dark energy is the quintessence field, which is essentially a slowly rolling scalar field. The equation of state for quintessence reads
$ p = w\rho $ , with$ p $ ,$ \rho $ , and$ w $ being the pressure, energy density, and the state parameter, respectively. To guarantee the cosmic acceleration and to satisfy the energy condition, the state parameter should be in the range$ -1<w<-1/3 $ . For relevant discussion on black holes surrounded by quintessence, see Refs. [62-80]. For example, in Ref. [80], the authors studied the effect of quintessence on the HP phase transitions for the Schwarzschild-AdS black hole and showed that quintessence always decreases with increase in the HP temperature.The basic motivation of our study of the HP phase transitions of the RN-qAdS black holes is twofold. First, there are critical phenomena for charged AdS black holes but not for neutral Schwarzschild-AdS black holes, because the critical pressure, volume, and temperature are all functions of the black hole charge [3]. Second, quintessence should be taken into account not only owing to its effect on the cosmic acceleration but also owing to its competition with the AdS background. Owing to the negative cosmological constant, the AdS background offers positive pressure and acts as a box in the universe. On the contrary, quintessence exerts negative pressure and thus effectively provides a repelling force. Therefore, it is quite interesting to compare the simultaneous impact of these two opposing components and to explore their overall influences on the HP phase transitions.
This paper is organized as follows. In Sect. II, we briefly describe the thermodynamic properties of the RN-qAdS black holes in the extended phase space. In Sect. III, the HP phase transitions are first analytically studied for the special case
$ w = -2/3 $ . In Sect. IV, the critical pressure, electric potential, and normalization factor are carefully discussed in order. Based on these critical values, the HP phase transitions with general state parameter$ w $ are investigated in Sect. V. Our conclusions are listed in Sect. VI. In this study, we work with the natural system of units and set$ c = G_{\rm N} = \hbar = k_{\rm B} = 1 $ . -
In this section, we first outline the thermodynamic properties of RN-qAdS black holes in the extended phase space and then discuss the HP phase transition in more detail.
-
We start from the action of an RN-qAdS black hole [63],
$ \frac{1}{16\pi}\int {{\rm{d}}}^4x\,\sqrt{-g} \left[ \left(R+ \frac{6}{l^2}-F_{\mu\nu}F^{\mu\nu} \right)+{\cal L}_{\rm q} \right], $

where
$ R $ is the Ricci scalar,$ F_{\mu\nu} $ is the electromagnetic tensor, and$ {\cal L}_{\rm q} $ is the Lagrangian of the quintessence dark energy, viewed as a barotropic perfect fluid,$ {\cal L}_{\rm q} = -\rho[1+w\ln({\rho}/{\rho_0})] $ , with$ \rho_0 $ being an integral constant. Consequently, the metric of the RN-qAdS black hole reads [62]$ {\rm d} s^2 = f(r)\,{\rm d} t^2-\frac{{\rm d} r^2}{f(r)}-r^2\,{\rm d}\theta^2-r^2 \sin^2{\theta}\, {\rm d} \phi^2, $

where
$ f(r) = 1-\frac{2M}{r}+\frac{Q^2}{r^2}+\frac{8\pi p r^2}{3}-\frac{a}{r^{1+3w}}, $

(2) with
$ M $ and$ Q $ being the black hole's mass and charge. The energy density of quintessence is normalized as$ \rho = - \frac{3wa}{2r^{3(1+w)}}, $

(3) where
$ a $ is a positive normalization factor. It will be shown later that there exists an upper bound for$ a $ , if the HP phase transition can occur.From Eq. (2), the event horizon radius
$ r_+ $ is determined as the largest root of$ f(r_{+}) = 0 $ . Then, the RN-qAdS black hole's mass can be expressed in terms of$ r_+ $ ,$ M = \frac{r_+}{2} \left(1+\frac{Q^2}{r_+^2}+\frac{8\pi p r_+^2}{3}-\frac{a}{r_+^{1+3w}} \right). $

To avoid naked singularity,
$ r_+ $ must be positive, which sets the lower bound on$ M $ as$ M>Q $ .Furthermore, the entropy of the RN-qAdS black hole can be obtained from the Bekenstein-Hawking equation as one quarter of the event horizon area
$ A $ [1,2],$ S = \frac{A}{4} = \pi r_+^2. $

(4) From Eqs. (1) and (4), the RN-qAdS black hole's mass can be reexpressed as a function of the thermodynamic variables
$ S $ ,$ p $ , and$ Q $ and the normalization factor$ a $ ,$ M = \frac 12\sqrt{ \frac S\pi} \left[1+ \frac{\pi Q^2}{S}+ \frac{8pS}{3}-a \left( \frac \pi S \right)^{\textstyle \frac{1+3w}{2}} \right]. $

(5) The first law of thermodynamics for the RN-qAdS black hole in the extended phase space can be obtained by directly differenting Eq. (5),
$ {{\rm{d}}} M = T\, {{\rm{d}}} S+V\, {{\rm{d}}} p+\Phi\, {{\rm{d}}} Q, $

(6) where
$ T $ ,$ V $ , and$ \Phi $ are the Hawking temperature, thermodynamic volume, and electric potential at the event horizon of the RN-qAdS black hole, respectively,$ T = \left( \frac{ \partial M}{ \partial S} \right)_{p,Q} = \frac{1}{4\sqrt{\pi S}} \left[1- \frac{\pi Q^2}{S}+8pS+3wa \left(\frac{\pi}{S} \right)^{\textstyle \frac{1+3w}{2}} \right], $

(7) $ V = \left( \frac{ \partial M}{ \partial p} \right)_{S,Q} = \frac{4\pi}{3} \left( \frac S\pi \right)^{ \frac 32}, $

(8) $ \Phi = \left( \frac{ \partial M}{ \partial Q} \right)_{S,p} = Q\sqrt{ \frac\pi S}. $

(9) Moreover, these results can be consistently rewritten in terms of
$ r_+ $ as$ T = \frac{f'(r_+)}{4\pi}, \quad V = \frac{4\pi r_+^3}{3}, \quad \Phi = \frac{Q}{r_+}. $

Thus, Eq. (7) becomes
$ T = \frac{1}{4\sqrt{\pi S}} \left[1-\Phi^2+8pS+3wa \left(\frac{\pi}{S} \right)^{\textstyle \frac{1+3w}{2}} \right]. $

(10) In addition, we find from Eq. (6) that the
$ p $ -$ V $ term has the form$ V\, {{\rm{d}}} p $ but not$ -p\, {{\rm{d}}} V $ . Therefore, the RN-qAdS black hole's mass$ M $ should be identified as its enthalpy rather than internal energy in the extended phase space.Last, the Smarr relation (i.e., the Gibbs–Duhem relation in traditional thermodynamics) can be obtained using a scaling argument as
$ M = 2TS-2pV+\Phi Q $ , consistent with the first law of black hole thermodynamics. In fact, this is one of the basic motivations to study the extended phase space, in which the cosmological constant varies, and the scaling argument thus applies.In our present work, the normalization factor
$ a $ is understood as a fixed parameter characterizing the energy density of the quintessence field. In addition, there are alternative interpretations of$ a $ as a thermodynamic variable [18,81-83]. Thus, the first law of black hole thermodynamics and the Smarr relation are generalized to$ {{\rm{d}}} M = T\, {{\rm{d}}} S+V\, {{\rm{d}}} p+\Phi\, {{\rm{d}}} Q+{\cal A}\, {{\rm{d}}} a $ and$ M = 2TS-2pV+ \Phi Q+(1+3w){\cal A}a $ , with$ {\cal A} $ being the conjugate variable of$ a $ ,$ {\cal A} = \left({ \partial M}/{ \partial a} \right)_{p,Q,S} = - \left({\pi}/{S} \right)^{{3w}/{2}}/2 $ . However, we stress that the specific forms of the first law and the Smarr relation depend on the choice of thermodynamic variables, and the choice of$ a $ as a thermodynamic variable is not unique. Nevertheless, we will show that the definition of the Gibbs free energy in our work is the same as in Refs. [18,81-83]; therefore, the discussion about the HP phase transition is consistent throughout and is not affected by the interpretation of the normalization factor$ a $ . -
Before discussing the HP phase transition, one important issue should be clarified in advance. Owing to the conservation of charge, a black hole with fixed charge cannot undergo the HP phase transition to the thermal AdS vacuum that is electrically neutral. Consequently, the HP phase transitions of RN-qAdS black holes should be studied in the grand canonical ensemble, in which the electric potential
$ \Phi $ is fixed, and the electric charge$ Q $ is thus allowed to vary.Since in the extended phase space the black hole's mass is regarded as enthalpy, the corresponding thermodynamic potential in the grand canonical ensemble should be the Gibbs free energy,
$ G(T,p,\Phi) = M-TS-\Phi Q. $

(11) Substituting Eqs. (5), (9), and (10) into Eq. (11), we obtain
$ G = \frac{1}{4}\sqrt{\frac{S}{\pi}} \left[1-\Phi^2-\frac{8pS}{3}-(2+3w)a \left(\frac{\pi}{S} \right)^{\textstyle \frac{1+3w}{2}} \right]. $

(12) Meanwhile, since the total number of the thermal gas particles in the AdS space is not conserved and can vary with temperature, the Gibbs free energy of the thermal AdS background is always 0.
Therefore, the criterion of the HP phase transition is that the Gibbs free energy of the black hole-thermal AdS system vanishes,
$ G = 0, $

(13) and the HP temperature
$ T_{\rm{HP}} $ is then fixed by Eq. (13) accordingly. In the following sections, the Gibbs free energy of the RN-qAdS black hole will be shown to monotonically decrease with temperature and will be negative above$ T_{\rm{HP}} $ . Therefore, below$ T_{\rm{HP}} $ , the thermal AdS phase with vanishing$ G $ is more stable; above$ T_{\rm{HP}} $ , the black hole phase with negative$ G $ is more preferred, and the thermal AdS gas is expected to collapse into the black hole. This interesting behavior indicates that the thermal AdS vacuum is more likely a solid rather than an ordinary gas in the HP phase transition [84]. -
The basic problems of relevance to the HP phase transitions include two aspects: determining the HP temperature
$ T_{\rm{HP}} $ and determining the Gibbs free energy$ G $ of the black hole-thermal AdS system as a function of temperature. First, at the HP phase transition point, Eq. (12) is substituted into the criterion in Eq. (13) to obtain the black hole entropy$ S $ in terms of$ p $ ,$ \Phi $ , and$ a $ , and then,$ S(p,\Phi,a) $ is substituted into Eq. (10) to obtain$ T_{\rm{HP}} $ . Next, we solve$ S $ from Eq. (10) as a function of$ T $ and then substitute it into Eq. (12) to obtain the$ G $ -$ T $ relation of the RN-qAdS black hole at arbitrary temperature, so as to achieve the global phase structure of the HP phase transition. Altogether, we choose the black hole entropy$ S $ as the intermediate variable in all of the following calculations. Clearly, it is equivalent to choosing the event horizon radius$ r_+ $ instead of$ S $ , as their simple relation is shown in Eq. (4).Generally speaking, the calculation of the RN-qAdS black hole entropy is difficult, as evident from the complicated expression in Eq. (12), and the analytical result is usually not available, unless the state parameter
$ w $ takes some special value. However, as we see from the last term in Eq. (12), when$ w = -2/3 $ [i.e., the middle point is in the range$ (-1,-1/3) $ ], the influence of quintessence on the Gibbs free energy vanishes, and the corresponding calculations are substantially simplified. Therefore, in this section we first explicitly analyze the special case$ w = -2/3 $ for mathematical clarity, investigating the effects of quintessence on the HP phase transitions, and move on to more general cases in the following sections.For
$ w = -2/3 $ , the relevant thermodynamic quantities in Eqs. (10) and (12) reduce to$ T = \frac{1}{4\pi} \left[\sqrt{\frac{\pi}{S}}(1-\Phi^2+8pS)-2a \right], $

(14) $ G = \frac{1}{4}\sqrt{\frac{S}{\pi}} \left(1-\Phi^2-\frac{8pS}{3} \right). $

(15) We observe from these results that, although quintessence does not affect the Gibbs free energy in the present circumstances, it does decrease the black hole temperature.
-
At the HP phase transition point,
$ G $ vanishes in Eq. (15), so we have$ S = 3(1-\Phi^2)/(8p) $ . Substituting$ S $ into Eq. (14), we obtain the HP temperature$ T_{\rm{HP}} $ ,$ T_{\rm{HP}} = \sqrt{\frac{8p}{3\pi}(1-\Phi^2)}-\frac{a}{2\pi}. $

(16) From Eq. (16), we clearly see that quintessence decreases
$ T_{\rm{HP}} $ , despite the fact that$ G $ is now irrelevant to$ a $ . If the HP phase transition occurs,$ T_{\rm{HP}} $ should be positive, and this requirement sets the corresponding bounds for$ p $ ,$ \Phi $ , and$ a $ , respectively, as follows:$ p>p_{\min} = \dfrac{3a^2}{32\pi(1-\Phi^2)}, $

(17) $ \Phi<\Phi_{\max} = \sqrt{1- \displaystyle\frac{3a^2}{32\pi p}}, $

(18) $ a<a_{\max} = \sqrt{\displaystyle\frac{32\pi p}{3}(1-\Phi^2)}. $

(19) The
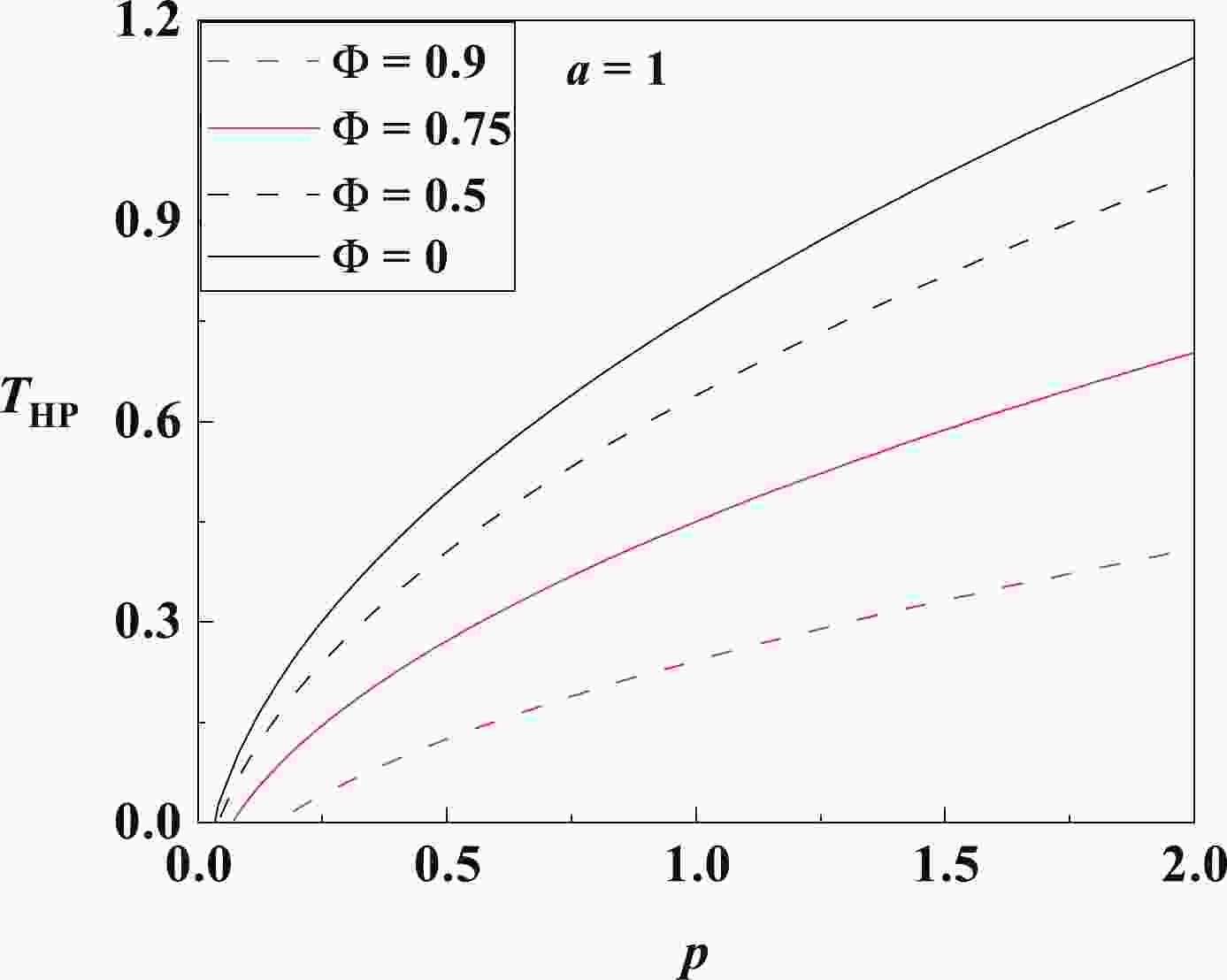
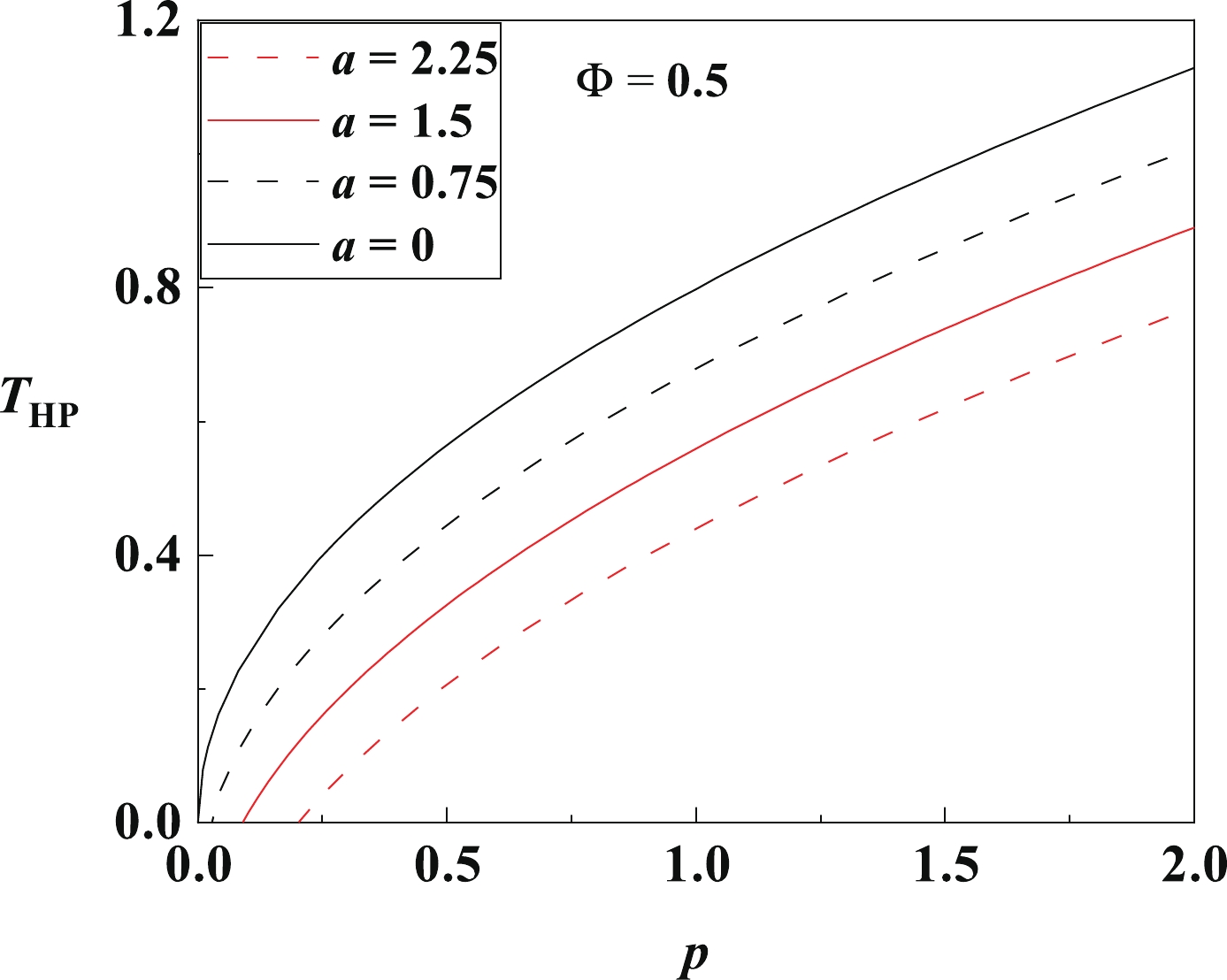
$ T_{\rm{HP}}-p $ curves of the RN-qAdS black holes, for different values of$ \Phi $ and$ a $ , are shown in Figs. 1 and 2. We find that the HP phase transition can occur at all high pressures, as there is no terminal point in the$ T_{\rm{HP}} $ –$ p $ curves (i.e., coexistence lines) in the phase diagram. In the low pressure limit,$ p $ has the lower bound$ p_\min $ . More interestingly, the thermal AdS phase lies below the coexistence line, meaning that it behaves like a solid at the HP phase transition. The HP temperature$ T_{\rm{HP}} $ increases with$ p $ and decreases with$ \Phi $ and$ a $ , consistent with the previous analyses in Ref. [61]. -
Next, for an arbitrary temperature, we first solve entropy
$ S $ from Eq. (14),$\begin{aligned}[b] S = & \frac{1}{32\pi p^{2} }\Big[(2 \pi T+a)^{2}-4\pi p(1-\Phi^{2}) \\ & \pm (2 \pi T+a)\sqrt{(2 \pi T+a)^2-8\pi p(1-\Phi^{2})}\Big]. \end{aligned} $

(20) There are two branches of
$ S $ in Eq. (20), corresponding to the stable large and unstable small black hole solutions, respectively. Substituting Eq. (20) into Eq. (15), we obtain the Gibbs free energies of the large and small RN-qAdS black holes as functions of$ T $ ,$ p $ ,$ \Phi $ , and$ a $ ,$ \begin{aligned} G = & -\frac{1}{192\sqrt{2}\pi^2p^2}\Big[(2 \pi T+a)^2-4\pi p(1-\Phi^2) \\ & \pm(2 \pi T+a) \sqrt{(2 \pi T+a)^{2}-8\pi p(1-\Phi^{2})}\Big]^{ \frac 12} \\ & \times \Big[(2 \pi T+a)^{2}-16 \pi p(1-\Phi^2) \\ & \pm(2 \pi T+a) \sqrt{(2 \pi T+a)^{2}-8 \pi p(1-\Phi^{2})}\Big]. \end{aligned} $

The
$ G $ -$ T $ curves of the stable large and unstable small RN-qAdS black holes with different values of$ p $ ,$ \Phi $ , and$ a $ are shown in Figs. 3–5. The$ G $ -$ T $ curves for the stable large RN-qAdS black holes intersect the$ T $ -axis at the HP temperature$ T_{\rm{HP}} $ . In Fig. 3, the intersection points move rightward, indicating that$ T_{\rm{HP}} $ increases with$ p $ . Similarly, in Figs. 4 and 5,$ T_{\rm{HP}} $ decreases with$ \Phi $ and$ a $ , as already shown in Figs. 1 and 2. Below or above$ T_{\rm{HP}} $ , the thermal AdS phase or the stable large black hole phase is globally preferred, respectively. The$ G $ -$ T $ curves of the unstable small RN-qAdS black holes are always above the$ T $ -axis, so the HP phase transition never occurs for them.
Figure 3. (color online) The Gibbs free energies
$G$ of the large and small RN-qAdS black holes as functions of temperature$T$ , for different pressures$p$ and fixed electric potential$\Phi = 0.5$ and normalization factor$a = 1$ . The HP temperature$T_{\rm{HP}}$ increases with$p$ . -
We continue to discuss the HP phase transitions of the RN-qAdS black holes for the general state parameter
$ w $ of quintessence. This generalization is physically straightforward but mathematically tedious. In most circumstances, the analytical results are unavailable, owing to the exponent$ (1+3w)/2 $ in Eqs. (10) and (12). Therefore, before going into details, we first consider the critical situation, when$ T_{\rm{HP}} = 0 $ and$ G = 0 $ simultaneously in Eqs. (10) and (12). Under such conditions, by eliminating the variable$ S $ , we obtain the following constraint on$ p $ ,$ \Phi $ ,$ a $ , and$ w $ ,$ \frac{3a(1+w)}{2(1-\Phi^2)} = \left[-\frac{(1+3w)(1-\Phi^2)}{8\pi p(1+w)} \right]^{\textstyle \frac{1+3w}{2}}. $

From the above constraint, the following expressions for the critical values
$ p_{\rm c} $ ,$ \Phi_{\rm c} $ , and$ a_{\rm c} $ , for the general state parameter$ w $ , can be easily obtained as$ p_{\rm c} = -\frac{1+3w}{8\pi} \left(\frac{2}{3a} \right)^{ \textstyle\frac{2}{1+3w}} \left(\frac{1-\Phi^2}{1+w} \right)^{\textstyle \frac{3(1+w)}{1+3w}}, $

(21) $ \Phi_{\rm c} = \sqrt{1-(1+w) \left(\frac{3a}{2} \right)^{ \textstyle\frac{2}{3(1+w)}} \left(-\frac{8\pi p}{1+3w} \right)^{\textstyle \frac{1+3 w}{3(1+ w)}}}, $

(22) $ a_{\rm c} = \frac{2}{3} \left(-\frac{1+3w}{8 \pi p} \right)^{\textstyle \frac{1+3w}{2}} \left(\frac{1-\Phi^2}{1+w} \right)^{\textstyle \frac{3(1+w)}{2}}. $

(23) These critical values are the natural extension of the results in Eqs. (17)–(19). Below, we discuss their dependence on
$ w $ in order, with special emphases on two limiting cases,$ w\to-1 $ and$ w\to-1/3 $ , where simple and analytical expressions exist. For general$ w $ , the results, obtained using numerical methods, are shown in Figs. 6–8 .
Figure 6. (color online) The critical pressure
$p_{\rm c}$ as a function of the state parameter$w$ , for different normalization factors$a$ and fixed electric potential$\Phi = 0.5$ . For$w\to-1$ , the limit of$p_{\rm c}$ is finite for any$\Phi$ and$a$ . For$w\to -1/3$ , if$a<0.75$ ,$p_{\rm c}$ monotonically decreases, with the limit$p_{\rm c}\to 0$ ; if$a>0.75$ ,$p_{\rm c}$ first decreases to the minimum and then increases to infinity. The curve with$a = 0.75$ is the boundary between these two branches. The HP phase transition can occur only in the region$p>p_{\rm c}$ .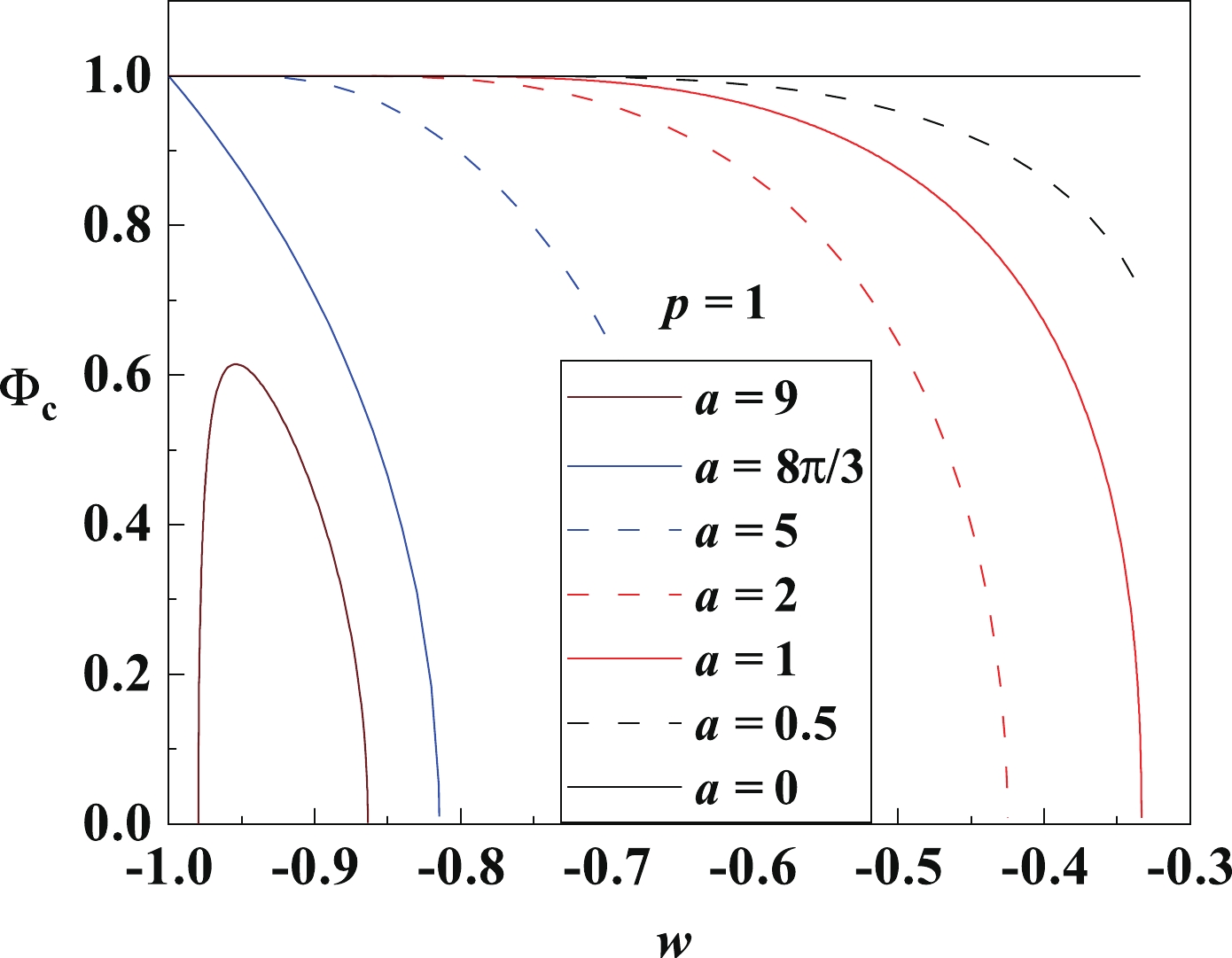
Figure 7. (color online) The critical electric potential
$\Phi_{\rm c}$ as a function of the state parameter$w$ , for different normalization factors$a$ and fixed pressure$p = 1$ . For$w\to-1$ ,$\Phi_{\rm c}$ first increases and then decreases with$w$ if$a>8\pi/3$ or monotonically decreases with$w$ if$a<8\pi/3$ . For$w\to-1/3$ ,$\Phi_{\rm c}$ monotonically decreases, but$w$ does not reach$-1/3$ unless$a<1$ . The HP phase transition can occur only in the region$\Phi<\Phi_{\rm c}$ .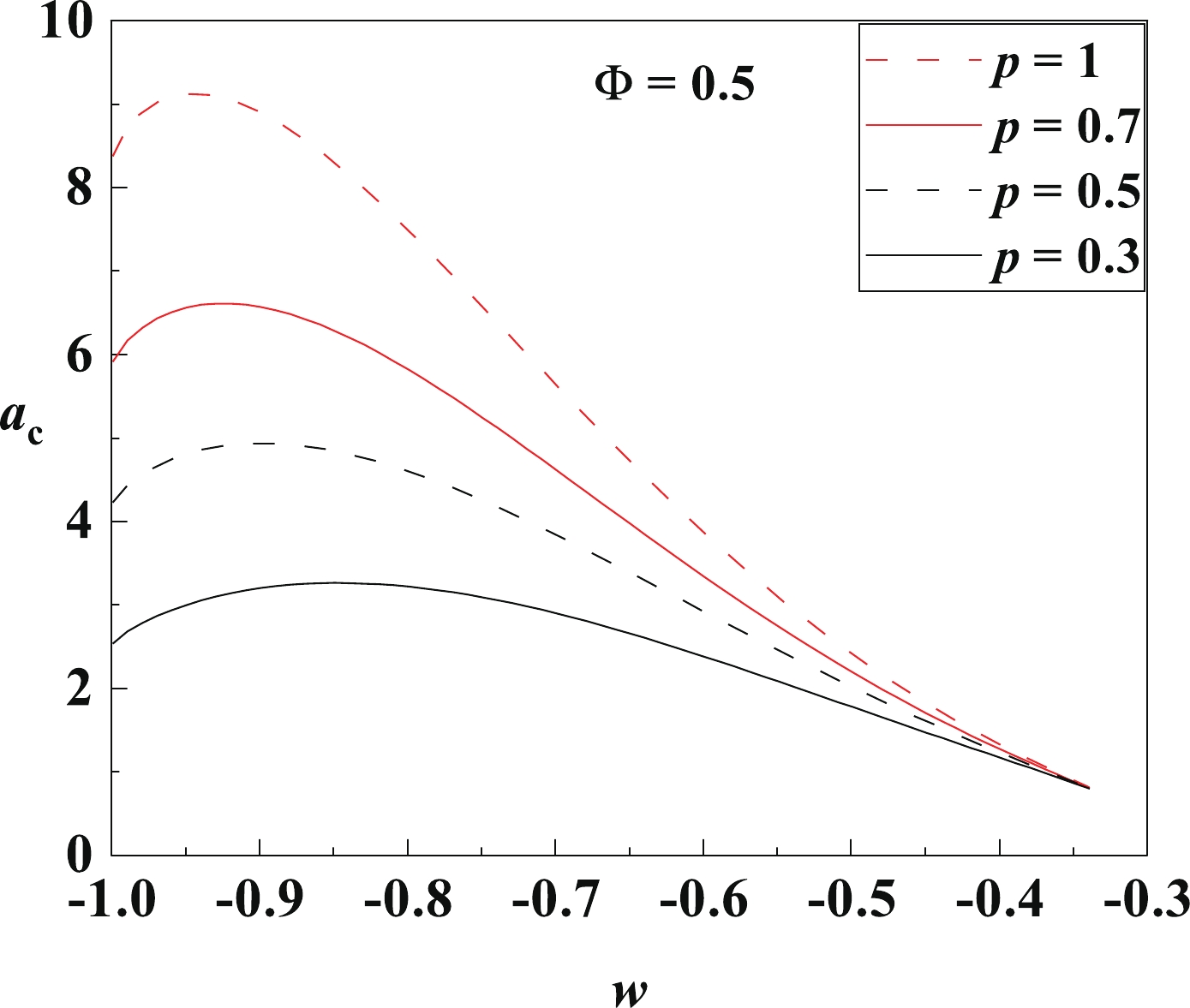
Figure 8. (color online) The critical normalization factor
$a_{\rm c}$ as a function of the state parameter$w$ , for different pressures$p$ and fixed electric potential$\Phi = 0.5$ . There always exists an upper bound for$a_{\rm c}$ when$-1<w<-1/3$ , and the HP phase transition can occur only in the region$a<a_{\rm c}$ . -
For the critical pressure
$ p_{\rm c} $ , in the limit$ w\to -1 $ , Eq. (21) reduces to$ p_{\rm c}\to \frac{3a}{8\pi} \left( \frac{1+w}{1-\Phi^2} \right)^{\textstyle \frac{3(1+w)}{2}}. $

In this case,
$ p_{\rm c} $ is bounded and reaches a finite value$ 3a/(8\pi) $ , independent of$ \Phi $ .In the limit
$ w\to-1/3 $ , Eq. (21) reduces to$ p_{\rm c}\to-\frac{1+3w}{8\pi} \left( \frac{1-\Phi^2}{a} \right)^{\textstyle \frac{2}{1+3w}}. $

In this case, the situation becomes more complex, and the complexity is attributed to the exponent
$ 2/(1+3w) $ . For$ w\to -1/3 $ , this exponent tends to negative infinity. Therefore, the limit of$ p_{\rm c} $ depends on the ratio$ (1-\Phi^2)/a $ . If$ a< 1-\Phi^2 $ , the ratio is greater than 1, so$ p_{\rm c}\to 0 $ . In contrast, if$ a>1-\Phi^2 $ , the ratio is less than 1, so$ p_{\rm c}\to\infty $ .The
$ p_{\rm c} $ –$ w $ curves are shown in Fig. 6. The HP phase transition can occur only when the pressure$ p $ is above the critical value$ p_{\rm c} $ for a given$ w $ , so there is always a minimal pressure in any$ T_{\rm{HP}} $ –$ p $ curve in Figs. 1 and 2. -
Next, for the critical electric potential
$ \Phi_{\rm c} $ , in the limit$ w\to -1 $ , Eq. (22) reduces to$ \Phi_{\rm c}\to\sqrt{1-(1+w) \left(\frac{3a}{8\pi p} \right)^{\textstyle \frac{2}{3(1+w)}}}. $

Now, the exponent
$ 2/[3(1+w)] $ tends to positive infinity. Therefore, the situation is similarly complex as that in Sect. IVA. If$ a<8\pi p/3 $ ,$ \Phi_{\rm c} $ decreases with$ w $ , with the limiting value$ \Phi_{\rm c}\to 1 $ . However, if$ a>8\pi p/3 $ , the situation is more complicated. Because the expression in the square root must be positive, the minimum of$ w $ actually cannot reach$ -1 $ . In this case,$ \Phi_{\rm c} $ first rapidly increases and then decreases with$ w $ .In the limit
$ w\to -1/3 $ , Eq. (22) reduces to$ \Phi_{\rm c}\to\sqrt{1-a \left(-\frac{8\pi p}{1+3w} \right)^{\textstyle \frac{1+3w}{2}}}. $

Again, the expression in the square root should be positive. It is evident that
$ \lim\limits_{w\to-1/3}\left(-\dfrac{8\pi p}{1+3w}\right)^{ \textstyle\frac{1+3w}{2}} = 1 $

and this limit is independent of
$ p $ . Therefore, if$ a<1 $ ,$ w $ can reach$ -1/3 $ , but if$ a>1 $ ,$ w $ actually cannot reach$ -1/3 $ .The
$ \Phi_{\rm c} $ –$ w $ curves are shown in Fig. 7. The HP phase transition can occur only when the electric potential$ \Phi $ is below the critical value$ \Phi_{\rm c} $ for a given$ w $ . -
Lastly, for the critical normalization factor
$ a_{\rm c} $ , in the limit$ w\to-1 $ , Eq. (23) reduces to$ a_{\rm c}\to\frac{8\pi p}{3} \left(\frac{1-\Phi^2}{1+w} \right)^{\textstyle \frac{3(1+w)}{2}}. $

In this case,
$ a_{\rm c} $ is bounded and reaches a finite value$ 8\pi p/3 $ , independent of$ \Phi $ .In the limit
$ w\to-1/3 $ , Eq. (23) reduces to$ a_{\rm c}\to(1-\Phi^2) \left(-\frac{1+3w}{8 \pi p} \right)^{\textstyle \frac{1+3w}{2}}. $

Similarly, in this case,
$ a_{\rm c} $ is also bounded and reaches a finite value$ 1-\Phi^2 $ , independent of$ p $ .The relationship between
$ a_{\rm c} $ and$ w $ needs more careful inspection. From the above two limiting cases, we find that$ a_{\rm c} $ first increases with$ w $ , reaching the maximal point at$ (w_0,a_{\rm c0}) $ , and then decreases with$ w $ . The exact values of$ w_0 $ and$ a_{\rm c0} $ can be obtained by setting$ {\partial a_{\rm c}}/{\partial w} = 0 $ in Eq. (23),$ w_0 = -\frac{1-\Phi^2+8\pi p}{3(1-\Phi^2)+8\pi p},\quad a_{\rm c0} = 1-\Phi^2+\frac{8\pi p}{3}. $

(24) These results indicate that for fixed
$ \Phi $ and$ p $ , if the HP phase transition occurs,$ a_{\rm c} $ should have an upper bound$ a_{\rm c0} $ . Then, it is evident that$ -1<w_0<-1/3 $ , meaning that this upper bound always exists for quintessence. Altogether,$ a_{\rm c} $ is not monotonic when$ -1<w<-1/3 $ , and this result is very important, when we analyze the effects of quintessence on the HP temperature$ T_{\rm{HP}} $ in the next section.The
$ a_{\rm c} $ –$ w $ curves are shown in Fig. 8. The HP phase transition can occur only when the normalization factor$ a $ is below the critical value$ a_{\rm c} $ for a given$ w $ .Let us summarize interim conclusions regarding the critical values. For a given state parameter
$ w $ , the HP phase transition can occur only for a large pressure$ p $ , small electric potential$ \Phi $ , and small normalization factor$ a $ (i.e.,$ p>p_{\rm c} $ ,$ \Phi<\Phi_{\rm c} $ , and$ a<a_{\rm c} $ ). Otherwise, the Gibbs free energy of the stable large RN-qAdS black hole is always less than that of the thermal AdS vacuum; accordingly, the HP phase transition cannot occur. -
Finally, we study the HP phase transitions of the RN-qAdS black holes in the extended phase space, for the most general state parameter
$ -1<w<-1/3 $ . In principle, the relevant calculations are similar to those in Sect. III, for the special value$ w = -2/3 $ . However, for general$ w $ , the last term in Eq. (12) can no longer be disregarded, making it impossible to obtain analytical results. Therefore, we used numerical methods to perform calculations, and we present our results below. -
To see the effects of quintessence on the HP temperature, we first show the
$ T_{\rm{HP}} $ –$ p $ curves in Fig. 9, for different$ a $ and for fixed$ \Phi $ and$ w $ . The curves are similar to those in Fig. 2 for$ w = -2/3 $ . The HP temperature$ T_{\rm{HP}} $ increases with pressure$ p $ , and$ p $ should be greater than its critical value$ p_{\rm c} $ . At a fixed pressure,$ T_{\rm{HP}} $ decreases with$ a $ , meaning that quintessence diminishes the HP temperature and thus induces the HP phase transition from the thermal AdS phase to the black hole phase at low temperatures. Therefore,$ a $ always has a maximum$ a_{\rm c} $ , since$ T_{\rm{HP}} $ should be positive.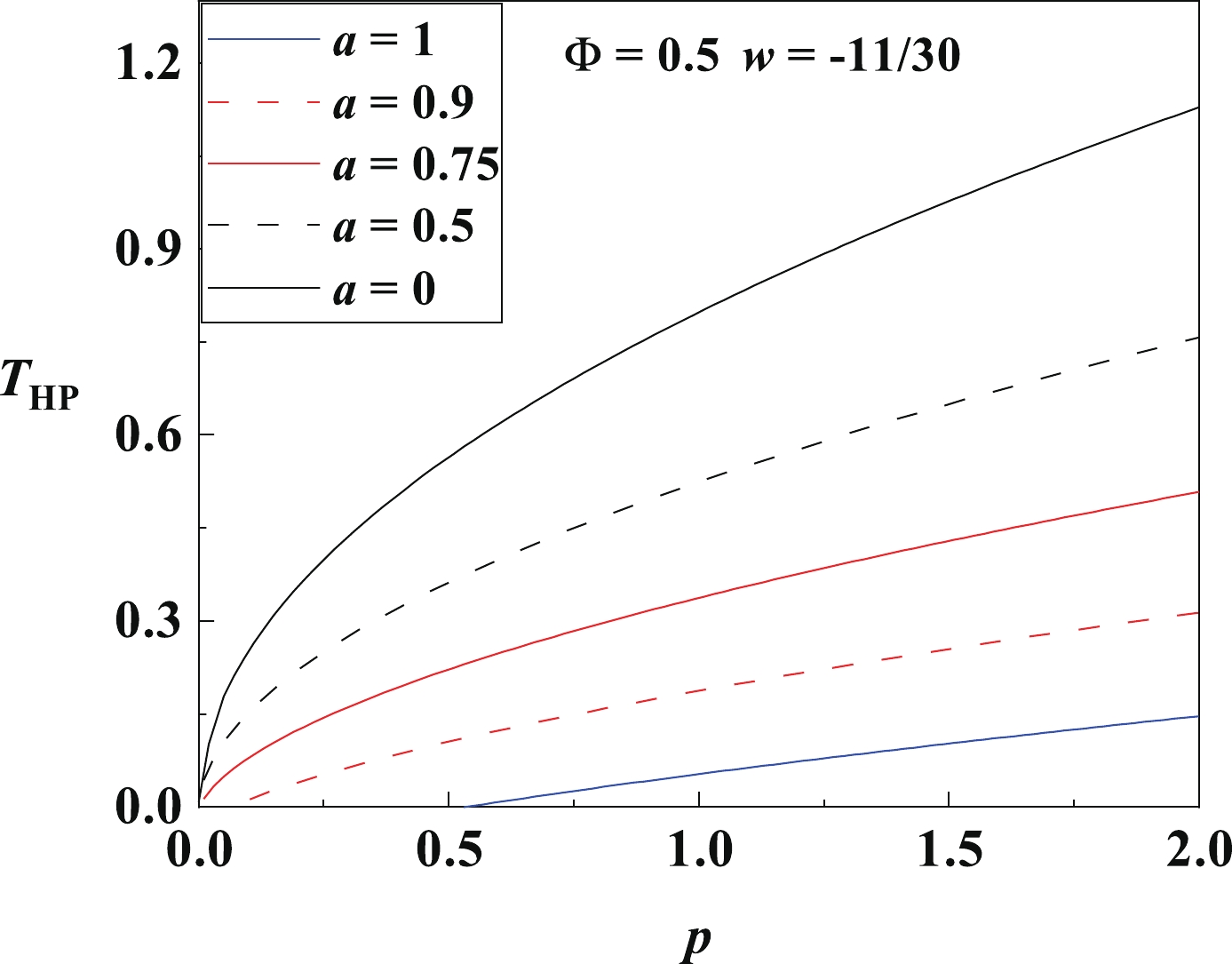
Figure 9. (color online) The HP temperature
$T_{\rm{HP}}$ as a function of pressure$p$ , for different normalization factors$a$ and fixed electric potential$\Phi = 0.5$ and state parameter$w = -11/30$ .$T_{\rm{HP}}$ decreases with$a$ , indicating that quintessence always tends to induce the HP phase transition at low temperatures.Next, we show the
$ T_{\rm{HP}} $ –$ p $ curves in Fig. 10, for different$ w $ and fixed$ \Phi $ and$ a $ . Again,$ T_{\rm{HP}} $ increases with pressure$ p $ , and$ p>p_{\rm c} $ . In most cases, at a fixed pressure,$ T_{\rm{HP}} $ decreases with$ w $ . However, it must be pointed out that, when$ w $ is close to$ -1 $ , two$ T_{\rm{HP}} $ –$ p $ curves can even intersect, and this intersection yields some unusual outcomes. First, two quintessence fields with different$ w $ but fixed$ p $ ,$ \Phi $ , and$ a $ can have the same HP temperature$ T_{\rm{HP}} $ . Second, when$ w $ is near$ -1 $ ,$ T_{\rm{HP}} $ increases with$ w $ (as explained in more detail in Fig. 11).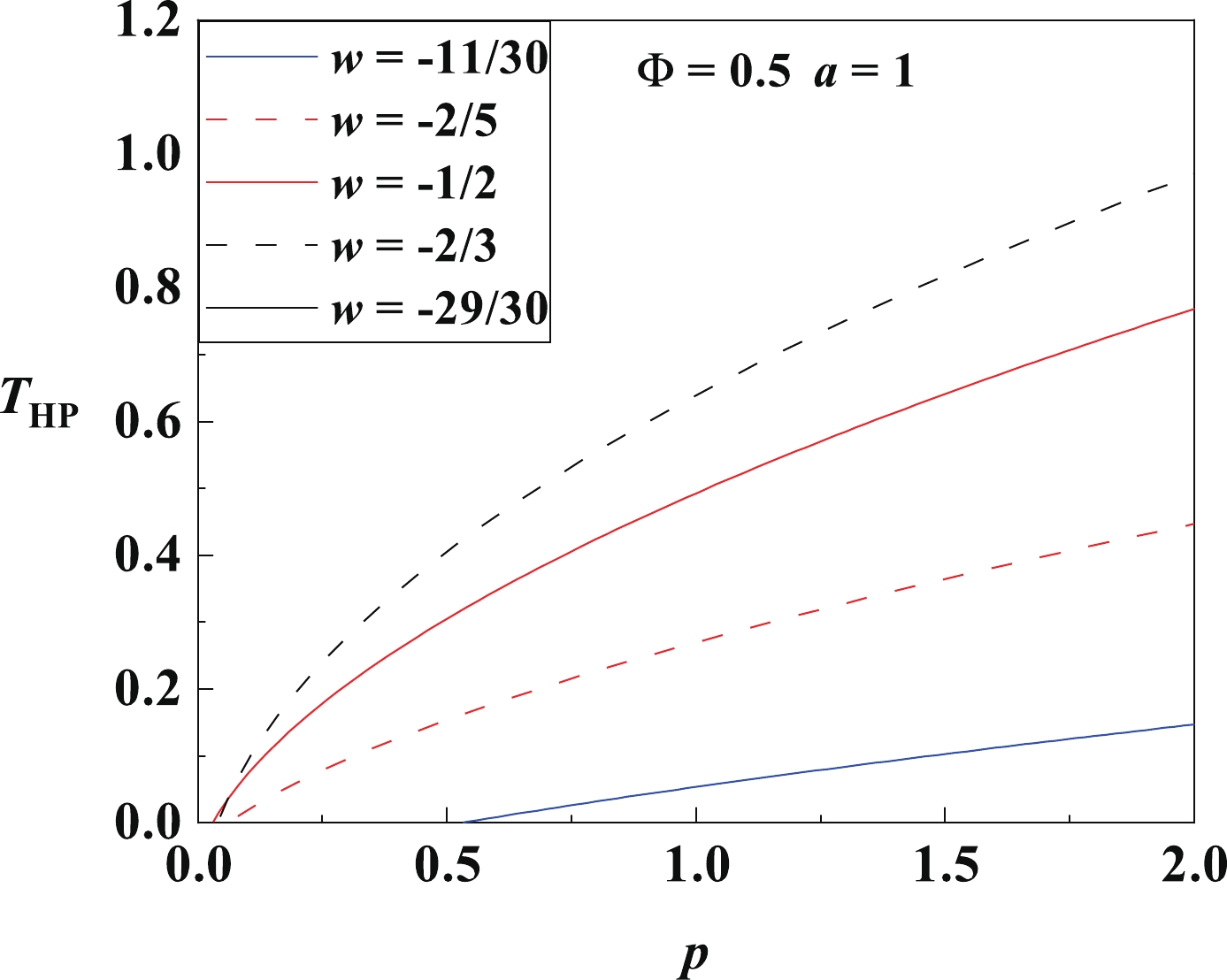
Figure 10. (color online) The HP temperature
$T_{\rm{HP}}$ as a function of pressure$p$ , for different state parameters$w$ and fixed electric potential$\Phi = 0.5$ and normalization factor$a = 1$ . In most cases,$T_{\rm{HP}}$ decreases with$w$ , but when$w$ is close to$-1$ , the curves with different$w$ can intersect, and$T_{\rm{HP}}$ may increase with$w$ .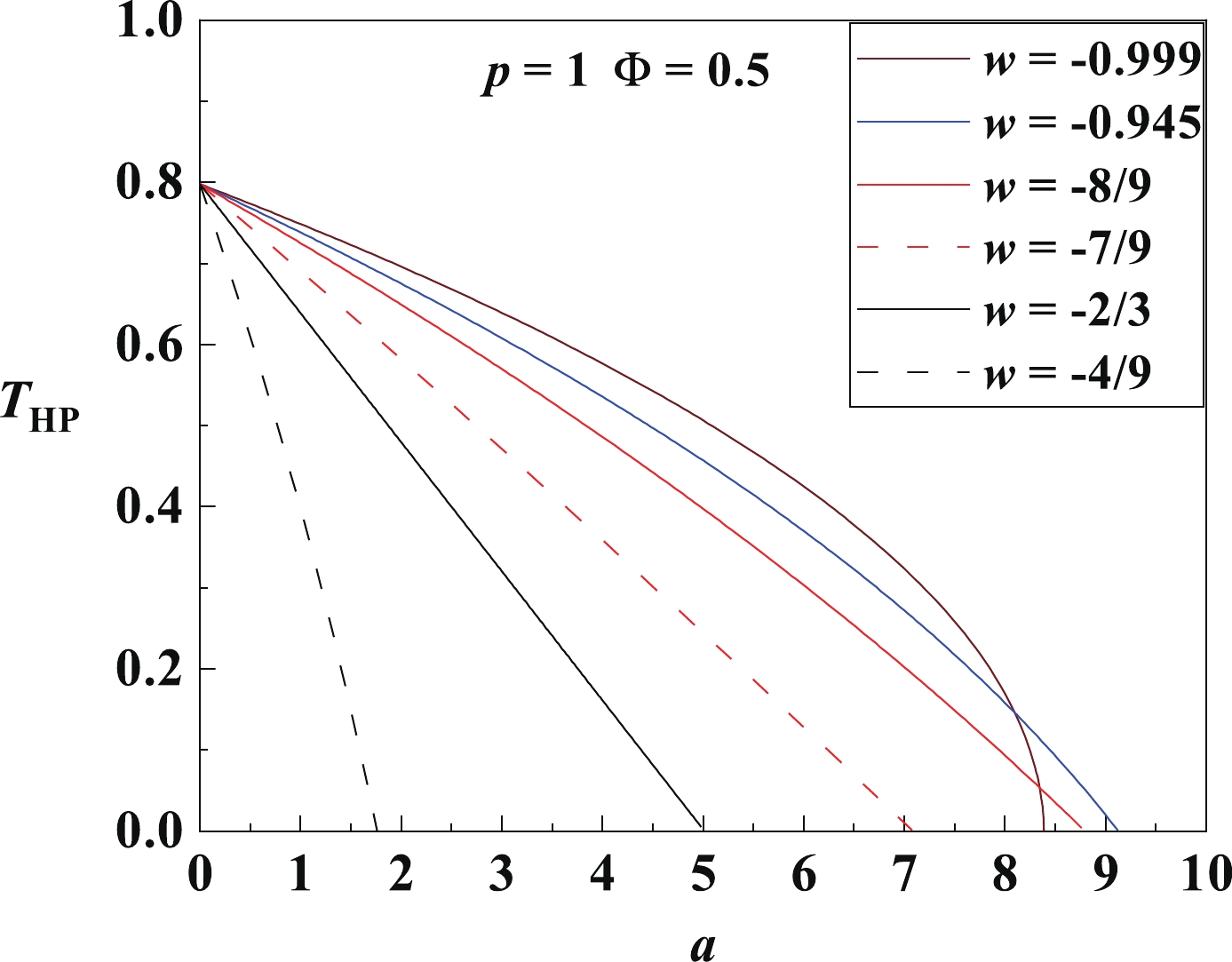
Figure 11. (color online) The HP temperature
$T_{\rm{HP}}$ as a function of normalization factor$a$ , for different state parameters$w$ and fixed pressure$p = 1$ and electric potential$\Phi = 0.5$ . All curves start from the same point at$(0,0.798)$ . When$w = -2/3$ , the$T_{\rm{HP}}$ –$a$ curve is a straight line, as indicated in Eq. (16). The curve with$w = w_0 = -0.945$ has the largest intercept$a_{\rm c0} = 9.128$ with the$a$ -axis. The different curves (e.g., the one with$w = -8/9$ and the one with$w = -0.999$ ) can intersect. Moreover, it can be seen that$T_{\rm{HP}}$ usually decreases with$w$ but may also increase with$w$ when$w$ is very close to -1.Below, we further investigate the dependence of
$ T_{\rm{HP}} $ on the two quintessence parameters,$ a $ and$ w $ . For simplicity, we show the$ T_{\rm{HP}} $ –$ a $ curves in Fig. 11, for different$ w $ and fixed$ p $ and$ \Phi $ . When$ a = 0 $ (i.e., without quintessence),$ T_{\rm{HP}} $ is entirely determined by$ p $ and$ \Phi $ . Therefore, all the$ T_{\rm{HP}} $ –$ a $ curves set out from the same starting point$ (0,\sqrt{8p(1-\Phi^2)/(3\pi)}) $ . When$ a\neq 0 $ , the situation is subtle and needs a better explanation. As explained in Eq. (24), for$ w = w_0 $ , the corresponding$ T_{\rm{HP}} $ –$ a $ curve has the largest intercept$ a_{\rm c0} $ with the$ a $ -axis. Hence, one$ T_{\rm{HP}} $ –$ a $ curve with$ w<w_0 $ can intersect with another for$ w>w_0 $ , as shown in Fig. 11, meaning that two RN-qAdS black holes with the same$ p $ ,$ \Phi $ , and$ a $ but different$ w $ can have the same HP temperature$ T_{\rm{HP}} $ . Furthermore, when$ w $ is even smaller and$ a $ is sufficiently large,$ T_{\rm{HP}} $ starts to increase with$ w $ , as shown in Fig. 10. -
Here, we show the
$ G $ -$ T $ curves of the stable large and unstable small RN-qAdS black holes in Fig. 12. As the cases with different values of$ p $ ,$ \Phi $ , and$ a $ have already been carefully studied in Sect. IIIB for$ w = -2/3 $ , we need not repeat them here, as the relevant results are qualitatively analogous for arbitrary$ w $ . Therefore, we focus on the Gibbs free energy, and vary the state parameter$ w $ while fixing the other parameters$ p $ ,$ \Phi $ , and$ a $ . With the special values of$ p $ ,$ \Phi $ , and$ a $ in Fig. 12, the HP temperature$ T_{\rm{HP}} $ monotonically decreases with$ w $ , consistent with the previous analysis in Fig. 11.
Figure 12. (color online) The Gibbs free energies
$G$ of the large and small RN-qAdS black holes as functions of temperature$T$ , for different values of the state parameter$w$ and fixed pressure$p = 1$ , electric potential$\Phi = 0.5$ , and normalization factor$a = 1$ . The HP temperature$T_{\rm{HP}}$ decreases with$w$ . -
Last, we discuss the general effects of quintessence on the HP temperature
$ T_{\rm{HP}} $ . For negative pressures, the quintessence field acts as a cold environment around the black hole. This property is exactly the opposite to that of the AdS vacuum, which offers a positive pressure. Since$ T_{\rm{HP}} $ in general increases with increasing pressure, the stronger the influence of quintessence, the lower the value of$ T_{\rm{HP}} $ .Let us consider the normalization condition in Eq. (3) at the event horizon radius
$ r_+ $ . The effects of quintessence are encoded in two parameters,$ a $ and$ w $ ,$ \rho = - \frac{3wa}{2r_+^{3(1+w)}}. $

(25) It is evident that the energy density
$ \rho $ of quintessence is proportional to the normalization factor$ a $ , so$ T_{\rm{HP}} $ always decreases with$ a $ , as already shown in Figs. 9 and 11.However, the dependence of
$ T_{\rm{HP}} $ on$ w $ is more intricate. Generally speaking, when$ a $ is small,$ T_{\rm{HP}} $ monotonically decreases with$ w $ , but when$ a $ is sufficiently large,$ T_{\rm{HP}} $ first increases and then decreases with$ w $ . We summarize these results in a 3-dimensional plot of$ T_{\rm{HP}} $ as a function of$ w $ and$ a $ in Fig. 13, for fixed pressure and electric potential. The projection of the counters with different$ a $ on the$ T_{\rm{HP}} $ –$ w $ plane explicitly exhibits the monotonicity of the$ T_{\rm{HP}} $ –$ w $ curves.
Figure 13. (color online) The HP temperature
$T_{\rm{HP}}$ as a function of the state parameter$w$ and normalization factor$a$ , for fixed pressure$p = 1$ and electric potential$\Phi = 0.5$ . The$T_{\rm{HP}}$ –$w$ curves can be directly produced by a projection of the counters with 8 different values of$a = 0$ , 0.5, 1, 2, 4, 7,$8\pi/3$ , and 8.8, and the monotonicity of the$T_{\rm{HP}}$ –$w$ curves can be observed explicitly. When$a<1$ ,$T_{\rm{HP}}$ monotonically decreases with$w$ . When$1<a<8\pi/3$ ,$T_{\rm{HP}}$ also monotonically decreases with$w$ , but$w$ can no longer reach$-1/3$ . When$a>8\pi/3$ ,$T_{\rm{HP}}$ first increases and then decreases with$w$ .It seems counterintuitive that
$ T_{\rm{HP}} $ may even decrease with$ w $ , because as$ w $ increases, the effect of quintessence becomes weaker, and$ T_{\rm{HP}} $ seems to increase accordingly, but actually it drops. However, there is no ambiguity at all. In fact, the dependence of$ \rho $ on$ w $ in Eq. (25) is not very simple, since$ w $ appears both in the numerator and in the denominator, so the relation of$ \rho $ and$ w $ also depends on$ r_+ $ . Using Eq. (4), we can rewrite Eq. (25) as$ \rho = - \frac{3wa}{2} \left( \frac\pi S \right)^{\textstyle \frac{3(1+w)}{2}}. $

Hence, when discussing the relationship between
$ \rho $ and$ w $ , we must take the special value of$ S $ into account.At the HP phase transition point, the corresponding entropy
$ S $ should be determined by setting$ G = 0 $ in Eq. (12),$ 1-\Phi^2-\frac{8pS}{3}-(2+3w)a \left(\frac{\pi}{S} \right)^{\textstyle \frac{1+3w}{2}} = 0. $

This equation is not analytically solvable, and we focus on the limiting cases with
$ w\to-1/3 $ and$ w\to-1 $ . First, when$ w\to-1/3 $ , we have$ S\to \frac{3(1-\Phi^2-a)}{8p}. $

If
$ p = 1 $ ,$ \Phi = 0.5 $ , and$ a $ is small, we find that$ S $ is also a small quantity of value approximately 0.2. In this case,$ \rho $ is an increasing function of$ w $ , so the influence of quintessence actually becomes stronger when$ w\to-1/3 $ , and the HP temperature$ T_{\rm{HP}} $ thus decreases with$ w $ , as shown in Fig. 13. Second, when$ w\to-1 $ , we have$ S\to \frac{3\pi(1-\Phi^2)}{8\pi p-3a}. $

If
$ p = 1 $ ,$ \Phi = 0.5 $ , and$ a $ is sufficiently large (e.g.,$ a = 8 $ around$ a_{\rm c0} $ ), we find that$ S $ is now a large quantity of value approximately 6. Thus,$ \rho $ now is a decreasing function of$ w $ , so$ T_{\rm{HP}} $ first increases with$ w $ and then decreases as before, when$ w $ is away from$ -1 $ . This behavior can be directly seen in Fig. 13 as well as from the intersection of the$ T_{\rm{HP}} $ –$ p $ curves in Fig. 10 and the intersection of the$ T_{\rm{HP}} $ –$ a $ curves in Fig. 11. -
The HP transition between the AdS black hole and the thermal AdS vacuum is an important issue in black hole thermodynamics. In this paper, the HP phase transitions of the charged AdS black holes surrounded by quintessence are systematically investigated in the extended phase space. On the one hand, the negative varying cosmological constant in the AdS space presents a positive thermodynamic pressure. On the other hand, the quintessence field, with the state parameter
$ -1<w<-1/3 $ , offers a negative pressure. Consequently, the HP phase transition is an overall result of these two competitive factors.The quintessence field modifies the metric of the RN-AdS black hole and thus influences black hole thermodynamics via introducing two new parameters, the normalization factor
$ a $ and the state parameter$ w $ . We calculate the HP temperature$ T_{\rm{HP}} $ as a function of$ p $ ,$ \Phi $ ,$ a $ , and$ w $ and also the Gibbs free energy$ G $ as a function of$ T $ ,$ \Phi $ ,$ a $ , and$ w $ . All the calculations are performed first for the special case of$ w = -2/3 $ and then for general$ w $ . The basic conclusions of our work are as follows:1. The HP temperature
$ T_{\rm{HP}} $ increases with pressure$ p $ , consistent with our previous work on the RN–AdS black holes in Ref. [61]. However, owing to the existence of quintessence,$ p $ should be greater than its critical value$ p_{\rm c} $ , such that$ T_{\rm{HP}} $ is positive.2. The Gibbs free energy
$ G $ of the RN-qAdS black hole decreases with$ T $ , so below or above$ T_{\rm{HP}} $ , the thermal AdS phase or the stable large RN-qAdS black hole phase is globally favored, respectively, which is also consistent with Ref. [61].3. When the HP phase transition happens, for the sake of positive
$ T_{\rm{HP}} $ , the variables$ p $ ,$ \Phi $ , and$ a $ cannot attain values higher than their critical values (i.e.,$ p>p_{\rm c} $ ,$ \Phi<\Phi_{\rm c} $ , and$ a<a_{\rm c} $ ). We plot$ p_{\rm c} $ ,$ \Phi_{\rm c} $ , and$ a_{\rm c} $ as functions of$ w $ in order in Sect. IV.4. The dependence of
$ T_{\rm{HP}} $ on the two quintessence parameters,$ a $ and$ w $ , is not quite so simple. First,$ T_{\rm{HP}} $ monotonically decreases with$ a $ . However,$ T_{\rm{HP}} $ decreases with$ w $ only when$ a $ is small. If$ a $ is sufficiently large,$ T_{\rm{HP}} $ first increases and then decreases with$ w $ . All these complexities arise from the relation of$ \rho $ and$ w $ in the normalization condition in Eq. (3). Nevertheless, whenever the energy density$ \rho $ of quintessence increases,$ T_{\rm{HP}} $ drops, so we are allowed to claim that the quintessence field always decreases$ T_{\rm{HP}} $ and facilitates the HP phase transition at low temperatures. This conclusion is consistent with the result in Ref. [80] and includes Ref. [80] as a limiting case of our work with$ \Phi = 0 $ .Altogether, we wish to present a whole picture of the HP phase transitions of the RN-qAdS black holes in the extended phase space. Evidently, it is straightforward to generalize this study to the rotating and charged rotating AdS black holes with quintessence. However, from our experience with Ref. [61], except the unnecessary mathematical inconvenience caused by rotation, we do not expect much new physical insight to be achieved.
-
We are very grateful to Bing-Yu Su, Yuan-Yuan Wang, and Zhi-Zhen Wang for fruitful discussions.
Hawking-Page phase transitions of charged AdS black holes surrounded by quintessence
- Received Date: 2020-06-03
- Available Online: 2021-01-15
Abstract: Hawking-Page phase transitions between the thermal anti-de Sitter vacuum and charged black holes surrounded by quintessence are studied in the extended phase space. The quintessence field, with the state parameter





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF





















 DownLoad:
DownLoad: