-
Nucleon-nucleon short-range correlation (NN-SRC) is one typical microscopic structure of the nucleus, resulting from a strong overlap of the wave functions of two nucleons. NN-SRC has attracted a lot of experimental interest in the last few decades, as it is an interesting, new phenomenon beyond the description of mean field theory [1-4], which has furthered our understanding of many-body problems and high density cold nuclear matter. The nucleons in NN-SRC strongly interact at a very short distance that is comparable with the nucleon radius. Kinematically, the two nucleons inside an SRC pair have large relative momenta; however, the center-of-mass (c.m.) momentum of the pair is small, of the value of the Fermi momentum [5-8]. The nucleons in the SRC pair have high momenta while the mass of the SRC pair is limited; hence, the nucleons in SRC are of high virtualities. Recently, the high momentum distribution of the SRC nucleon was explained successfully under a generalized contact formalism (GCF) arising from the universal contact term of fermion interaction at high momentum [9-11]. Moreover, SRC pairing has some influence on the nucleon structure and properties, as the nucleons in an SRC pair interact strongly.
Experimental evidence for SRC comes from exclusive [5-8,12-14] and inclusive measurements [15-18] of quasi-elastic scattering between a probe and an SRC pair, showing back-to-back high momentum motions of two final nucleons. The exclusive measurements find that approximately 90% of NN-SRC pairs are proton-neutron pairs [6,13,14,19], which may explain the difference between the proton momentum distribution and the neutron momentum distribution in a proton-neutron imbalanced system. The pn-pair dominance in the SRC configurations indicates that the SRC pairing is induced by a strong tensor force [20-22].
Nucleon mass is a fundamental aspect in particle and nuclear physics. However, its origins are still under discussion [23-25], with few experimental tests. As the nucleon is not an elementary particle, its bulk properties should be derived from the dynamics of its constituents. In the Standard Model, the underlying theory describing the nucleon is quantum chromodynamics (QCD). The extraordinary features of QCD – confinement and asymptotic freedom – make the exact solution of a system of hadron size unavailable. Nonetheless, with the development of computing technology, lattice QCD (LQCD) has achieved some interesting numerical results on nucleon mass decomposition [26,27], despite providing few insights into the underlying physics. According to analysis of QCD energy-momentum tensor, the nucleon mass is composed of four terms: the quark mass term
$M_{{m}}$ , quark energy term$M_{{q}}$ , gluon energy term$M_{{g}}$ , and trace anomaly term$M_{{a}}$ [23,24]. The trace anomaly only appears in the renormalization of loop diagrams. In the MIT bag model, there is a clear physical picture. The nucleon mass is attributed to the internal energies of the massless particles (quarks and gluons) and the vacuum energy of the "bag" volume [28,29]. The conceptually simple assumption of the MIT bag model is that the fields are confined to a finite space, which actually captures the confinement property of QCD.On the experimental side, it is essential to look for a measuring method and choice of data that are sensitive to the nucleon mass structure. The nucleus is made of nucleons and therefore naturally provides a good platform to study the nucleonic properties. The interaction between nucleons can be exploited to probe quark and gluon dynamics. Nowadays, electron-ion colliders are widely discussed worldwide [30-33]. They will solve several mysteries regarding nuclear effects and nucleon structure. Determining the mass of a nucleon that interacts strongly with a neighboring nucleon may shed some light on the origin of the nucleon mass and the characteristics of nonperturbative QCD. In this letter, we extract the nucleon mass in NN-SRC as well as the number of SRC pairs in a deuteron, based on inclusive measurements of high energy electron-nucleus scattering.
To search for NN-SRC using high energy electron-nucleus scattering, one measures the nucleons at momenta larger than the Fermi momentum. In electron-nucleus interaction, a virtual photon is exchanged between the electron and the nucleus, and the Bjorken variable
$ x_{\rm{B}} = Q^2/(2m_{\rm{N}}\nu) $ is determined by the photon kinematics.$ Q^2 $ and$ \nu $ represent the negative values of the photon's four momentum square and the energy of the photon in the nucleus's rest frame, respectively. For the definition of the Bjorken variable in experiment,$m_{{N}} = 0.938$ MeV is taken to be the mass of the free nucleon. Usually, the requirement$ 1.5<x_{{B}}<2 $ is applied to select the quasi-elastic scattering of the electron on the NN-SRC pair [15-18]. The nuclear cross-section for quasi-elastic scattering on a NN-SRC pair is$ \sigma_{{A}}(Q^2, x_{{B}}\sim 2) = A\frac{\hat{a}_2(A)}{2} \sigma_{{2N}}(Q^2, x_{{B}}\sim 2), $

(1) where
$ \hat{a}_2(A) $ represents the probability of a nucleon being in an NN-SRC configuration,$\sigma_{{2N}}(Q^2, x_{{B}}\sim 2)$ is the cross-section for the electron-SRC pair scattering, and$ A $ is the mass number of the nucleus. Instead of measuring the absolute cross-section, the cross-section ratio is usually measured experimentally to explore the nuclear effects and to reduce the systematic uncertainty. The SRC cross-section ratio$ a_2(A) $ is defined as$ a_2(A) = \frac{\sigma_{{A}}(Q^2, x_{{B}}\sim 2)/A}{\sigma_{{D}}(Q^2, x_{{B}}\sim 2)/2}, $

(2) where the deuteron (D) is the reference nucleus. The properties of NN-SRC pairs in different nuclei are said to be universal if the SRC ratio
$ a_2(A) $ has no kinematical dependences in the SRC region. In this case Eq. (1) yields$ a_2(A) = \frac{\hat{a}_2(A)}{\hat{a}_2(D)}, $

(3) which is independent of the kinematic variables
$ Q^2 $ and$x_{{B}}$ , commonly called the "scaling" [15-18]. The "scaling" of the ratio$ a_2 $ is observed at JLab using a high energy and high intensity electron beam. Note that a high$ Q^2 $ ($ Q^2>1 $ GeV2) is needed to reduce the final-state interactions, and small$ \nu $ is required to reduce the contamination by inelastic scattering [17]. In the review article on hard probes of NN-SRC [3], a moderate momentum transfer (1 GeV2<Q2< 4 GeV2) is suggested to avoid the long-range two-body interactions and the contributions from$ \Delta $ -isobars. The energy of the virtual photon is required to be much larger than the nucleon-nucleon potential. The kinematical conditions on well separation of two-nucleon and three-nucleon SRCs are also discussed in literature [3], providing good guidance for the experiments.The measured SRC ratio
$ a_2(A) $ connects to the relative number of SRC pairs per nucleon, as the scattering at$x_{{B}}\sim 2$ is dominantly attributed to the scattering between the electron and the NN-SRC pairs. Therefore, the number of NN-SRC pairs in a nucleus (of mass number$ A $ ) is expressed as the product of the measured SRC ratio$ a_2 $ and the number of SRC pairs in a deuteron, as shown in Eq. (4).$ \begin{aligned}[b] a_2(A) =& \frac{n^{{A}}_{\rm{SRC}}/A}{n^{{d}}_{\rm{SRC}}/2},\\ n^{{A}}_{\rm{SRC}} =& A \times a_2(A) \times \frac{n^{{d}}_{\rm{SRC}}}{2}. \end{aligned} $

(4) We make the approximation that both the nucleon mass in a NN-SRC pair (
$ m_{\rm{SRC}} $ ) and the nucleon mass in the mean-field ($ m_{\rm{MF}} $ ) are universal for all nuclei. The nuclear mass is then decomposed into two terms:$ M(A,Z) = 2n^{{A}}_{\rm{SRC}}m_{\rm{SRC}}+(A-2n^{{A}}_{\rm{SRC}})m_{\rm{MF}}. $

(5) Here, the mass of the SRC nucleon is defined as half the mass of the SRC pair. Combining Eqs. (4) and (5), we obtain the following decomposition of the nuclear mass per nucleon:
$ \frac{M(A,Z)}{A} = m_{\rm{MF}}+a_2(A)n^{{d}}_{\rm{SRC}} (m_{\rm{SRC}}-m_{\rm{MF}}). $

(6) For the deuteron, the SRC ratio
$ a_2(D) $ is one; hence, we have a constraining condition,$ \frac{M^{{d}}}{2} = m_{\rm{MF}}+n^{{d}}_{\rm{SRC}} (m_{\rm{SRC}}-m_{\rm{MF}}), $

(7) for the nuclear mass decomposition expressed by Eq. (6). From Eq. (7), we obtain
$ m_{\rm{MF}} $ in terms of$n^{{d}}_{\rm{SRC}}$ and$ m_{\rm{SRC}} $ . Substituting$ m_{\rm{MF}} $ expressed in terms of$n^{{d}}_{\rm{SRC}}$ and$ m_{\rm{SRC}} $ into Eq. (6), we finally find the nuclear mass per nucleon as a function of$ a_2(A) $ , with two free parameters$n^{{d}}_{\rm{SRC}}$ and$ m_{\rm{SRC}} $ ,$\begin{aligned}[b] \frac{M(A,Z)}{A} =& \frac{M^{{d}}}{2(1-n^{{d}}_{\rm{SRC}})} -\frac{n^{{d}}_{\rm{SRC}}}{1-n^{{d}}_{\rm{SRC}}}m_{\rm{SRC}} \\ &+a_2(A)\left[ \frac{n^{{d}}_{\rm{SRC}}}{1-n^{{d}}_{\rm{SRC}}}m_{\rm{SRC}} - \frac{M^{{d}}n^{{d}}_{\rm{SRC}}}{2(1-n^{{d}}_{\rm{SRC}})} \right].\end{aligned} $

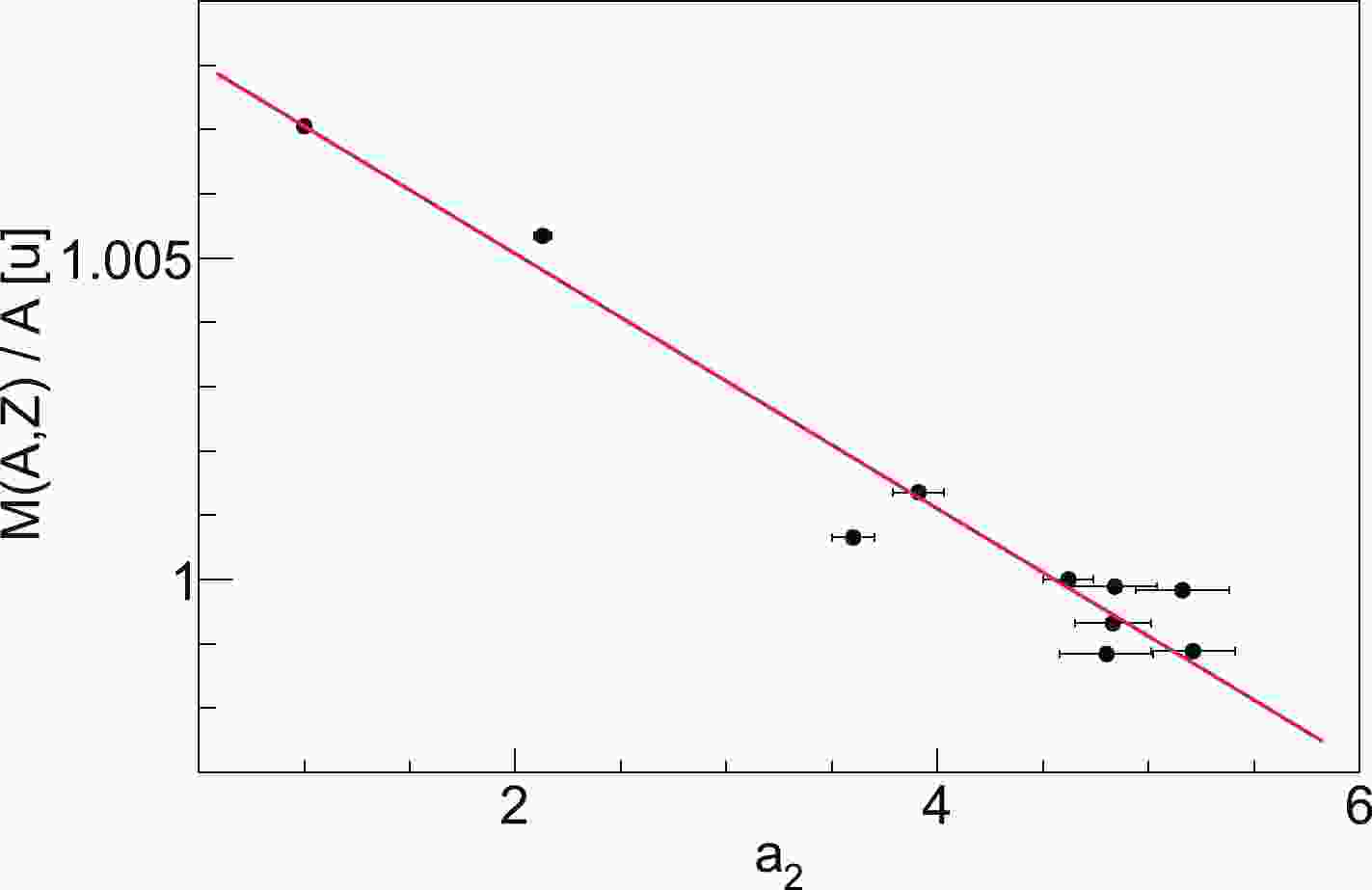
(8) The nuclear mass as a function of
$ a_2 $ is shown in Fig. 1. The nuclear masses are taken from Refs. [34,35], and the$ a_2 $ data are taken from the combination of the two analyses [18,36] of different experimental measurements [15-17]. A linear fit is performed to the mass-$ a_2 $ correlation using Eq. (8). All current data are approximately distributed around the fit. The quality of the fit is$ \chi^2/N = 95/9 = 10.5 $ . The nucleon mass in an NN-SRC pair is found to be$ m_{\rm{SRC}} = 0.915\pm 0.019 $ u = 852±18 MeV, and the number of SRC pairs in a deuteron is$n^{{d}}_{\rm{SRC}} = 0.021\pm 0.005$ . Applying Eq. (7), we obtain the mean-field nucleon mass$ m_{\rm{MF}} = 1.009\pm 0.005 $ u = 939.9 ± 5 MeV. Currently, a theoretical calculation from the GCF method shows that there is at least 20% uncertainty when using the$ a_2 $ data as the empirical SRC pair abundances [11]. Therefore, the fit quality of the mass-$ a_2 $ correlation could be improved if these model uncertainties larger than 20% are included in the analysis. The quality of the fit is reduced to$ \chi^2/N = 1.6/9 = 0.2 $ if the additional uncertainties of 20% are considered in the analysis.Regardless of the additional uncertainty of 20% mentioned above for
$ a_2 $ data interpretation, we speculate that there are two other reasons that the quality of the fit is not good. First, the mean-field nucleon mass is not universal for all nuclei. Second, there are more terms in addition to the nuclear mass decomposition in Eq. (5), such as the nucleon mass resulting from multiple-nucleon short-range correlations (more than two nucleons). The density of a light nucleus is quite different from that of a heavy one; hence, the mean-field nucleon mass of a light nucleus possibly exhibits a sizeable difference. If we exclude the data of 3He and 4He when performing the fit, we obtain a high quality of fit$ \chi^2/N = 9.1/7 = 1.3 $ . At the same time, the obtained nucleon mass in SRC and the number of NN-SRCs are almost unchanged.Regarding two nucleon bags merging into one nucleon bag, the volume of two nucleons is reduced by the volume of one nucleon bag. Therefore, for two completely overlapping nucleons, the vacuum energy is reduced by the vacuum energy of one nucleon bag. In the MIT bag model, in the relativistic-gas approximation, the volume of a stable "bag" is
$ V\approx B^{-3/4} $ , where$ B $ is the vacuum energy per unit volume. The vacuum energy of one nucleon bag is then estimated to be$ BV\approx B^{1/4} $ . Based on an analysis of the baryon ground state,$ B^{1/4} $ is fit to be approximately 120 MeV [28]. As a result, the mass loss per nucleon in an NN-SRC pair is predicted to be$ B^{1/4}/2 = 60 $ MeV, which is denoted as bag model-I in this work. In this model,$ B = (0.12)^4 $ GeV4 = 0.027 GeV fm-3 also equals the external pressure at the "bag" boundary, which is actually close to the preliminary result of the pressure inside a proton$ p(r = 0.85\; {\rm{fm}})\sim 0.04 $ GeV fm-3 in a recent analysis of generalized parton distribution functions from DVCS experiments [37]. The equilibrium condition and the relativistic-gas approximation in the bag model give$ \begin{aligned}[b] p =& \frac{1}{3}\frac{E_r}{V} = B,\\ E =& E_r+BV = 4BV, \end{aligned} $

(9) where
$ E_r $ is the internal energy carried by quarks and gluons, and$ E $ is the total energy [29]. Therefore, based on the equilibrium condition (Eq. (9)), the vacuum energy of one nucleon is$BV = E/4 = m_{{N}}/4$ . This gives the mass loss per nucleon in an NN-SRC pair as$m_{{N}}/8$ = 117 MeV, labeled as bag model-II in this work.In QCD theory, the trace anomaly contribution
$M_{{a}}$ to the nucleon mass is analogous to the vacuum energy in the MIT bag model, i.e., the vacuum energy of one nucleon bag. The energy loss (mass deficit) of NN-SRC equals the trace anomaly contribution$M_{{a}}$ , as the volume reduction of the extremely strong NN-SRC configuration is the volume of one nucleon, rather than that of two free nucleons. The vacuum energy loss per nucleon is therefore half the trace anomaly contribution to the nucleon mass. According to an LQCD calculation [27] on the QCD trace anomaly, this corresponds to a mass loss per paired nucleon of$M_{{a}}/2 = 108$ MeV. Based on this assumption concerning the trace anomaly, the mass loss of a nucleon in a 3N-SRC is$2M_{{a}}/3$ , that in a 4N-SRC is$3M_{{a}}/4$ , and so on.Although the mesons are not the fundamental degrees of freedom in QCD, they give a good approximation of the nuclear force at low energy. The quark-meson coupling (QMC) model, a mean-field description of non-overlapping nucleon bags bound by the self-consistent exchange of mesons, predicts an effective nucleon mass of 775~801 MeV in nuclear matter at saturation density, with the structure effects of both the nucleon and the mesons considered [38]. Hence, the effective nucleon mass in the nuclear environment of high density imposes some new constraints on the parameters of the QMC model, such as the various meson-quark couplings and the nucleon form factors in nuclear matter.
To sum up, Table 1 lists the values of the mass deficit of an NN-SRC nucleon from this analysis and some models. In our analysis of
$ a_2 $ data, each nucleon in an NN-SRC pair loses a mass of 86 ± 18 MeV. We find that our extracted value of the nucleon mass loss in an NN-SRC state is consistent with the QCD trace anomaly part of nucleon mass and the MIT bag model predictions.Table 1. Mass deficits of a nucleon in NN-SRC from this work and some models. See the main text for detailed explanations.
The number of SRC pairs in a deuteron is an interesting quantity, which tells us the probability of the nucleon being in a short-distance configuration. From our fit, the nucleons in a deuteron have approximately 2.1% probability of forming an SRC pair. The nuclear tensor force that dominates at medium distance plays a crucial role in the formation of pn-SRC pairs. Therefore, the exact probability of pn-SRC pairing in a deuteron places some significant constraints on the details of the tensor force. This can be studied with future numerical calculations based on an
$ ab\; initio $ method or an effective method such as that using the GCF model. Using Eq. (4), we calculate the number of pn-SRC pairs in 12C to be$n_{\rm{SRC}}^{{C}} = 0.58\pm 0.14$ , with the obtained$n^{{d}}_{\rm{SRC}} = 0.021\pm 0.005$ . Based on our analysis, 9.7% ± 2.4% of the nucleons in 12C are in the NN-SRC state, which is smaller than previous estimations [6,16].In summary, we have obtained the nucleon mass in NN-SRC, which shows that the nucleon in an SRC pair has a large mass deficit of approximately 86 MeV, in agreement with QCD decomposition of the nucleon mass and MIT bag model predictions. One feature of NN-SRC is the high momentum of the nucleon inside the pair, which actually requires a far off-shell SRC nucleon. Moreover, we also find the number of NN-SRC pairs in a deuteron to be
$ 0.021\pm 0.005 $ , from the correlation between the nuclear mass and the SRC ratio$ a_2(A) $ . Our analysis suggests that approximately 9.7% ± 2.4% of the nucleons are in pn-SRC configurations for the commonly studied nucleus 12C.
HTML
-
We thank Dr. Jarah Evslin for reading the manuscript and helping in improving the English writing.





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF
























 DownLoad:
DownLoad: