-
Energetic partons produced at early stages of relativistic heavy-ion collisions (HIC) may lose substantial energy through interacting with quark-gluon plasma (QGP), a novel nuclear medium formed in these collisions under extreme conditions of high temperature and energy density. This phenomenon is known as jet quenching [1-3] and can provide promising tools to investigate the creation and properties of QGP. In the last decade, experimental and theoretical studies of jet quenching have been extended from the suppression of leading hadron productions [4-15] to medium modifications of a wealth of full jet observables, such as inclusive jets, di-jets, gauge boson tagged jets, heavy flavor jets, and jet substructures [16-50]. A full jet is a collimated spray of final-state hadrons in
$ e^+e^- $ collisions, elementary hadron-hadron collisions, and nucleus-nucleus reactions with large center-of-mass colliding energies. The existence of QGP should naturally alter the yields and internal structures of a full jet, and thus, the medium modifications of jet observables can be used for tomography of the nuclear matter formed in HIC.One interesting jet substructure observable is jet girth (or angularity), which probes the radiation inside a jet [51-55]. The medium modification of jet girth may help us better understand the specific features of jet-medium interaction by providing complementary aspects of the jet fragmentation such as jet transverse momentum distribution and shed light on how the jet substructure is resolved by the medium in HIC. Recently, the ALICE Collaboration measured the normalized girth distributions for inclusive jets with small-radius (
$ R = 0.2 $ ) in heavy-ion collisions [52], which further facilitated the studies of girth in HIC because the theoretical model calculations can now be confronted directly with the data to infer crucial information on jet propagation in the QCD medium.In this work, we present our study on the normalized distributions of girth for both inclusive jets and
$ Z^0 $ tagged jets with jet radius$ R = 0.2 $ in Pb+Pb collisions at$ \sqrt{s} = 2.76 $ TeV. We utilize POWHEG+PYTHIA [56-58], a model matching next-to-leading order (NLO) with parton showering (PS), including hadronization in the final state, to obtain the solid baseline calculations of jet girth in p+p collisions, which are then combined with a numerical simulation of parton energy loss within the higher-twist approach of jet quenching [59-62] to compute the girth distribution in high-energy nuclear collisions. Our numerical results of girth distribution for inclusive jets give satisfactory descriptions of ALICE data in both p+p and Pb+Pb collisions, where we observe a shift of girth distribution to lower values in Pb+Pb relative to that in p+p. The girth distributions of$ Z^0+{\rm jet} $ in Pb+Pb collisions at the LHC are calculated for the first time, which show that medium modifications of girth distributions for$ Z^0+{\rm jet} $ are less pronounced than those for inclusive jets.This paper is organized as follows. In Sec. II, we introduce the framework of computing the normalized distributions of girth in detail in p+p and Pb+Pb collisions. The numerical results and detailed discussions of the medium modifications of girth in inclusive jets and gauge boson
$ Z^0 $ tagged jets are presented in Sec. III. Finally, Sec. IV summarizes our study. -
We study a jet substructure observable, the girth, which characterizes the radial distribution of radiation inside a jet [51, 52] and is defined as
$ g = \sum\limits_{i}\frac{p_{T,i}}{p_{T,{\rm jet}}}\left| \Delta R_{i,{\rm jet}}\right|, $

(1) where
$ p_{T,i} $ stands for the transverse momentum of the ith constituent inside the jet with transverse momentum$ p_{T,{\rm jet}} $ .$ \Delta R_{(i,{\rm jet})} $ denotes the distance in$ (\eta,\phi) $ space between this constituent and the jet axis. Girth is sensitive to the radial energy profile of the jet, and for a fixed jet$ p_T $ , the jet is more collimated with a lower value of girth.In this paper, a Monte Carlo model POWHEG+PYTHIA, with next-to-leading order (NLO) matrix elements matched with parton showering [56-58], is used to simulate hadron productions in p+p collisions. In our simulation the POWHEG BOX code is utilized [57, 58], which provides a computer framework for implementing NLO calculations in parton shower Monte Carlo programs according to the POWHEG scheme [63]. It has been shown that the POWHEG BOX Monte Carlo program matched with parton showering can accurately describe productions and correlations for a variety of processes, such as single-top production, di-jets, gauge boson+jets, and multiple jets [64]. We generate the NLO matrix elements for QCD di-jet processes with POWHEG BOX and then match them with PYTHIA to simulate parton showering and hadronization [65]. The Fastjet package [66] is used to reconstruct final state hadrons into full jets.
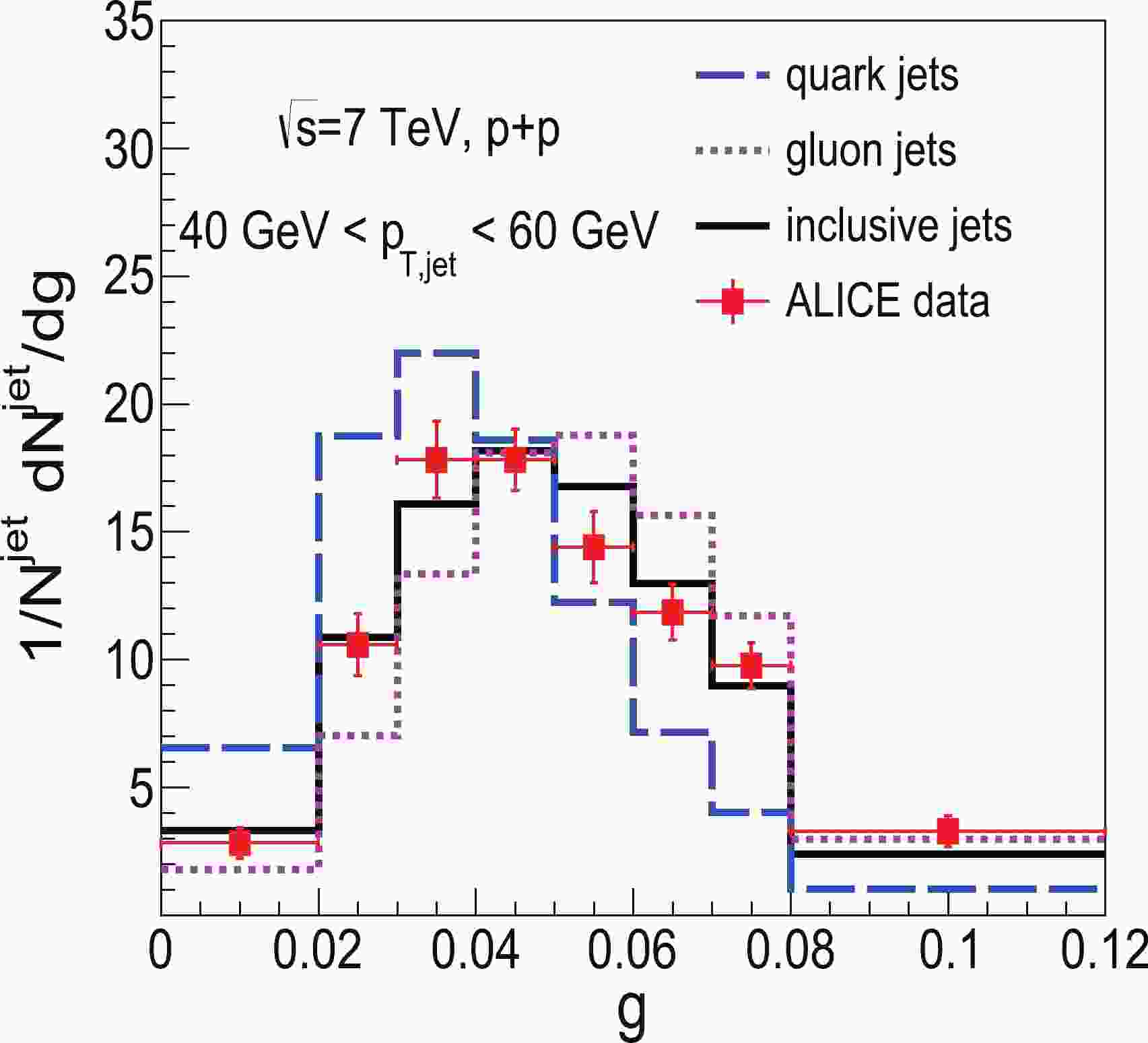
To compare with experimental data, events are selected within the same kinematic cuts as imposed in the experimental measurements, which we use for the comparison. In ALICE Collaboration data, jets are reconstructed by the anti-
$ k_{T} $ algorithm with a small radius$ R = 0.2 $ from charged tracks where a cutoff with$ p_{T}>0.15 $ GeV is imposed. The transverse momentum of jets is required to be$ 40 \ {\rm GeV} <p_{T, \rm jet}<60 $ GeV in the central rapidity region$ \left|\eta_{\rm jet}\right|<0.7 $ . Our simulation results of normalized distributions of girth in p+p collisions at$ \sqrt{s} = 7 $ TeV and their comparison with ALICE data are plotted in Fig. 1. One can observe that POWHEG+PYTHIA calculation can provide reasonable descriptions of girth distributions in p+p collisions in the overall region, which will serve as a baseline for the subsequent study of nuclear modification in heavy-ion collisions. We also plot the girth distributions of quark-initiated and gluon-initiated jets, at$ \sqrt{s} = 7 $ TeV, in Fig. 1. We observe that, at the same jet$ p_T $ , the girth distributions of gluon jets are broader than those of quark jets, and the peak of girth distribution for gluon jets is located at larger g relative to that for quark jets. This implies that, compared to quark jets, gluon jets have larger radiation width and favor harder radiation with wider radiation angle, on average.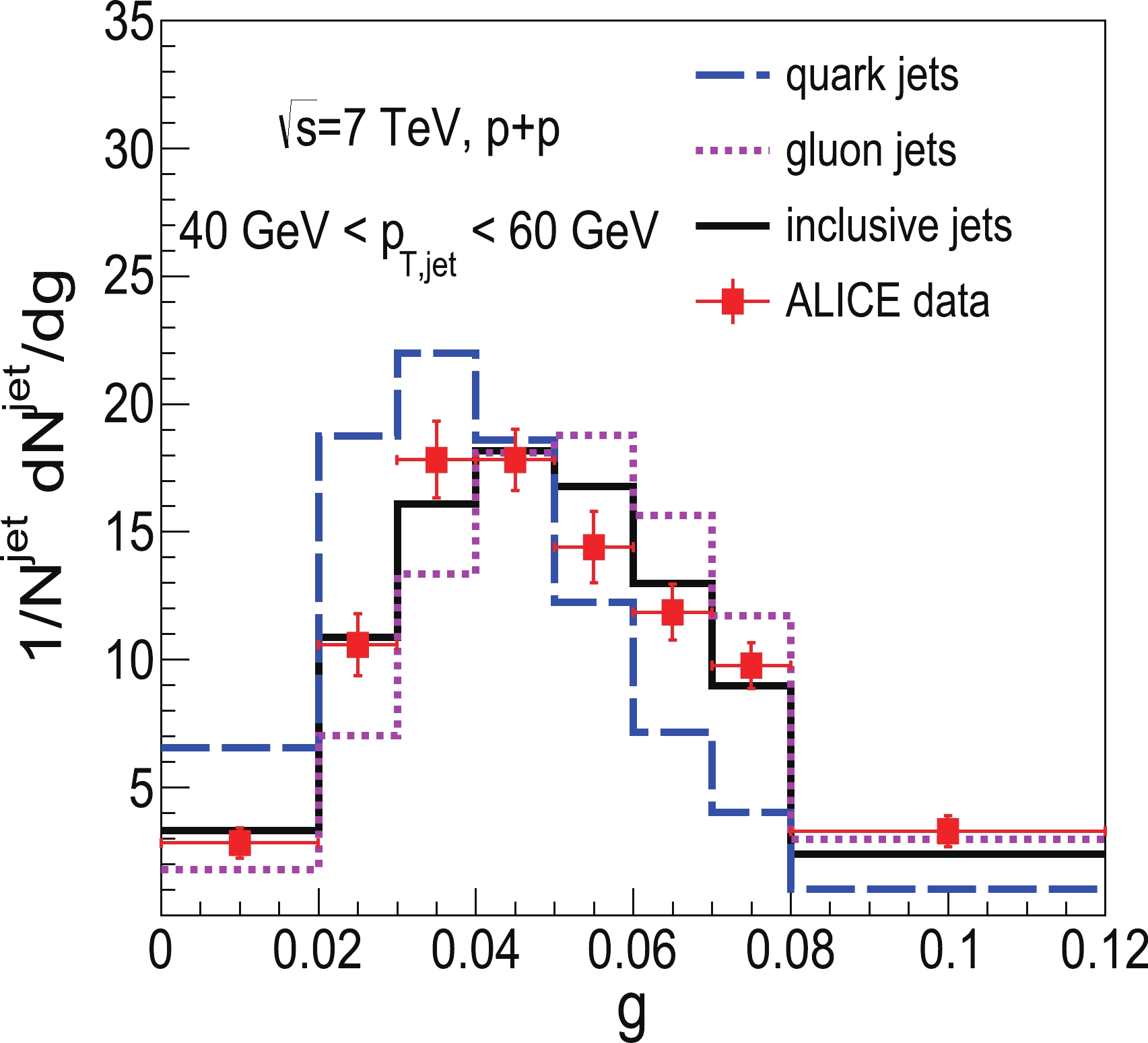
Figure 1. (color online) Normalized girth distribution for inclusive jets in p+p collisions at
$\sqrt{s}=7$ TeV from POWHEG+PYTHIA calculation compared with ALICE data [52].In heavy-ion collisions, partons produced from hard scattering will lose their energy due to jet-medium interactions. In our analysis framework, with the initial jet shower partons generated by POWHEG+PYTHIA and the initial position of these partons in QGP sampled from the Glauber model [67], they propagate through the QGP step-by-step after its formation. The probability of gluon radiation occurring in QGP during a time step
$ \Delta t $ can be expressed as [48, 68-70]:$ P_{\rm rad}(t,\Delta t) = 1-{\rm e}^{-\left\langle N(t,\Delta t)\right\rangle} \, , $

(2) where
$ \left\langle N(t,\Delta t)\right\rangle $ is the average number of emitted gluons integrated from the medium induced radiated gluon spectrum within the higher-twist (HT) approach [59-62]:$ \frac{{\rm d}N}{{\rm d}x{\rm d}k^{2}_{\perp}{\rm d}t} = \frac{2\alpha_{s}C_sP(x)\hat{q}}{\pi k^{4}_{\perp}}\sin^2\left(\frac{t-t_i}{2\tau_f}\right)\left(\frac{k^2_{\perp}}{k^2_{\perp}+x^2M^2}\right)^4, $

(3) where
$ \alpha_{s} $ is the strong coupling constant, M is the mass of the parent parton, x denotes the energy fraction relative to the mother parton, and$ k_\perp $ gives the transverse momentum of the radiated gluon. We have applied a lower energy cut-off for the emitted gluon$ x_{\rm min} = \mu_{D}/E $ in the calculation, with$ \mu_{D} $ the Debye screening mass.$ C_s $ is the Casimir factor for quarks ($ C_F $ ) and gluons ($ C_A $ ),$ P(x) $ stands for the splitting function in a vacuum, and$ \tau_f = 2Ex(1-x)/(k^2_\perp+x^2M^2) $ is the formation time of the radiated gluons. The jet transport parameter$ \hat{q} $ is proportional to the local parton density distribution in the QCD medium and related to the space and time evolution of the medium relative to its initial value$ \hat{q}_0 $ in the central region when QGP formed, which controls the magnitude of energy loss due to jet-medium interaction.Multiple gluon radiation is allowed during each time step, where the number of radiated gluons is assumed to follow a Poisson distribution. The values of x and
$ k_\perp $ could be sampled according to the radiative gluon spectrum in Eq. (3). A hard thermal loop (HTL) approximation formula [71]$ \dfrac{{\rm d}E^{\rm coll}}{{\rm d}t} = \dfrac{\alpha_{s}C_{s}\mu^{2}_{D}}{2}{\rm ln}\dfrac{\sqrt{ET}}{\mu_{D}} $ is adopted to simulate the collisional energy loss of the showered partons [45, 48]. The evolution profile of the QGP medium is provided by the smooth iEBE-VISHNU hydro model [72]. In our simulation,$ \hat{q}_{0} = 1.2 $ GeV2/fm is directly extracted from the sophisticated study of the identified hadron suppression in Pb+Pb collisions at 2.76 TeV using the same evolved QGP medium expansion [14]. Therefore, an effective jet transport parameter and$ \hat{q} $ that only consider jet transport in the QGP phase are used. Jet partons stop their propagation on the freeze-out hypersurface of the fireball ($ T_c = 165 $ MeV). After all the partons have propagated through the QGP, the PYQUEN method is used to preform the hadronization process [73, 74]. In the model, the radiated gluons are rearranged in the same string as their parent partons, and these partons can fragment into hadrons via a standard PYTHIA hadronization procedure. -
We can now calculate the jet number normalized girth distributions in Pb+Pb collisions at
$ \sqrt{s} = 2.76 $ TeV. We apply the same kinematic cuts as we did in the p+p collisions in the previous section. Shown in Fig. 2 are our numerical results for girth distributions for inclusive jets with radius$ R = 0.2 $ , which are confronted against ALICE measurements [52]. Satisfactory agreement can be found between our theoretical calculations and experimental data. Compared with that in p+p collisions, the observed girth distribution in Pb+Pb is shifted to lower values of g due to jet-medium interactions, which implies that a jet in Pb+Pb may exhibit smaller radiation width and have softer fragments than those in p+p collisions.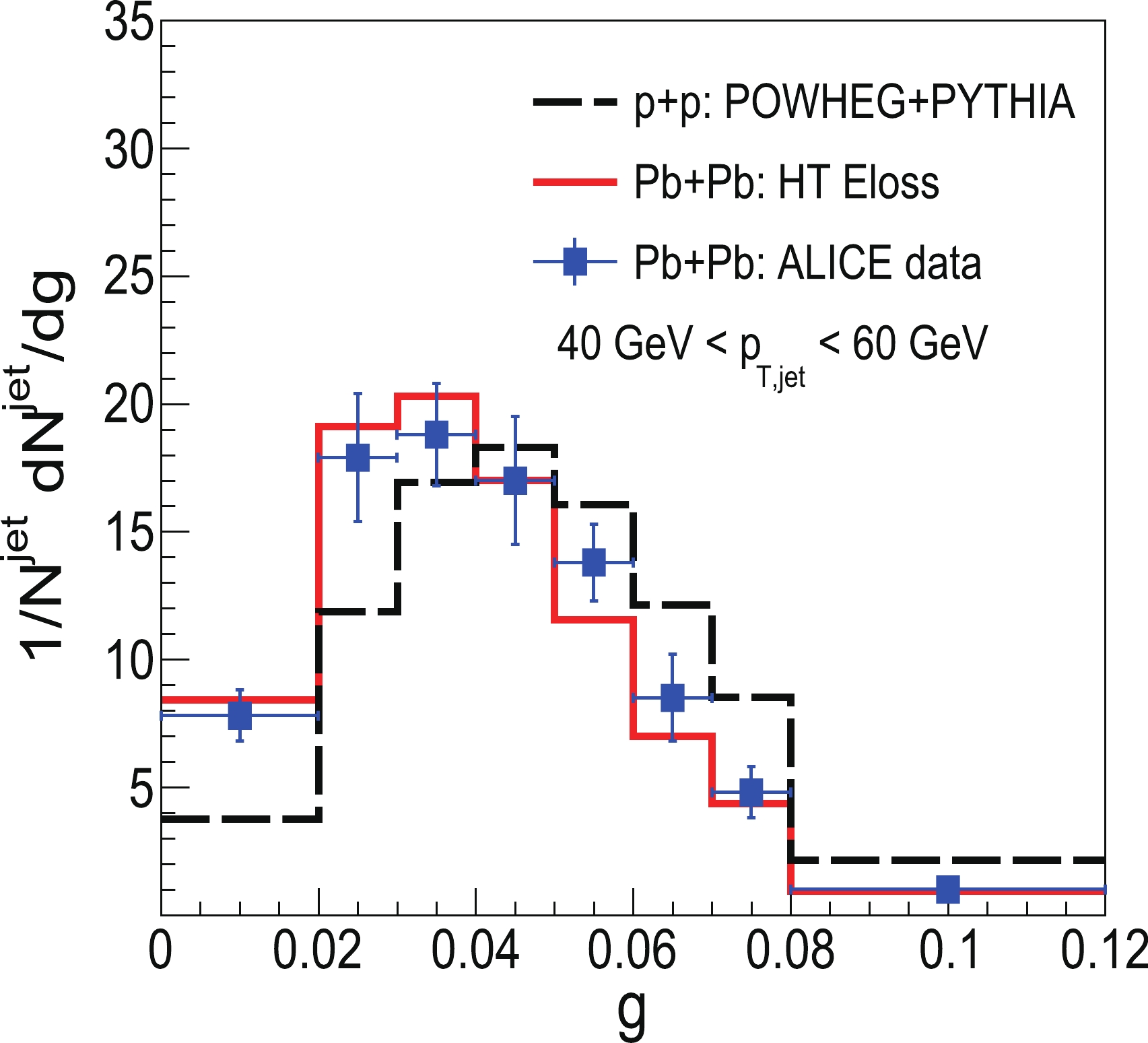
Figure 2. (color online) Normalized girth distributions of inclusive jets in p+p and Pb+Pb collisions at
$\sqrt{s}=2.76$ TeV compared with ALICE data [52].To compare the difference between girth distributions in HIC and those in p+p in a more straightforward way, we can plot numerically the nuclear modification ratio of girth distributions
$ R_{AA}^{\rm girth} $ , which is defined as$ R_{AA}^{\rm girth} = {\dfrac{1}{N_{AA}} \dfrac{{\rm d}N_{AA}}{{\rm d}g}}\Bigg/{\dfrac{1}{N_{pp}} \dfrac{{\rm d}N_{pp}}{{\rm d}g}} \,\, . $

(4) Fig. 3 are the
$ R_{AA}^{\rm girth} $ of jet number normalized girth distributions for inclusive jets, as well as the components of inclusive jets, i.e., quark jets and gluon jets. One can see an enhancement of girth distribution for both quark jets and gluon jets in small g regions but a suppression in large g regions. Moreover, the nuclear modification for gluon jet girth distribution is stronger than that for quark jets. Because inclusive jets consist of both gluon jets and quark jets, it is natural to observe that the curve of$ R_{AA}^{\rm girth} $ for inclusive jets lies between the curve of$ R_{AA}^{\rm girth} $ for gluon jets and that for quark jets. The overall shift of girth distribution for gluon jets and quark jets results from the softer hadron fragments in these jets in HIC, as we demonstrate in detail later.
Figure 3. (color online) Nuclear modification ratio of girth distribution of inclusive jets and quark and gluon jets. The ratio from the ALICE Collaboration is preformed by Pb+Pb measurements scaled by MC simulation in p+p [52].
Another reason underlying the nuclear modification of girth distribution for inclusive jets is the change in relative fraction of quark and gluon jets. In the higher-twist formalism of parton energy loss (as in most other models of jet quenching), gluons may suffer more energy loss than quarks in the QCD medium with its larger color charge. Therefore, generally, we should observe an increase in the relative fraction of quark jets in A+A relative to p+p collisions, and because the girth distribution of quark jets is spread over a smaller g region compared to that of gluon jets, as illustrated in Fig. 1, the individual impacts of fraction changes of quark jets and gluon jets to form inclusive jets will increase the girth distribution of inclusive jets at small g and decrease it at large g. This is depicted in Fig. 3, where the curve labelled "inclusive jets: q/g fraction alteration" represents the numerical result of
$ R_{AA}^{\rm girth} $ by only considering the effect of quark/gluon jet fraction changes due to energy loss while assuming there are no medium modifications for girth distributions of pure gluon jets and quark jets in heavy-ion collisions.To see the time evolution of jet girth distribution in QGP, we plot
$ R_{AA}^{\rm girth} $ values for gluon jets as an example at time steps$ \tau = 1,2,3,4 $ GeV and their comparison with full evolution in Fig. 4. One can observe that, when jets suffer energy loss, there is an enhancement of girth distribution in small g regions but a suppression in large g regions. The nuclear modifications will gradually become more visible as jet propagations in QGP.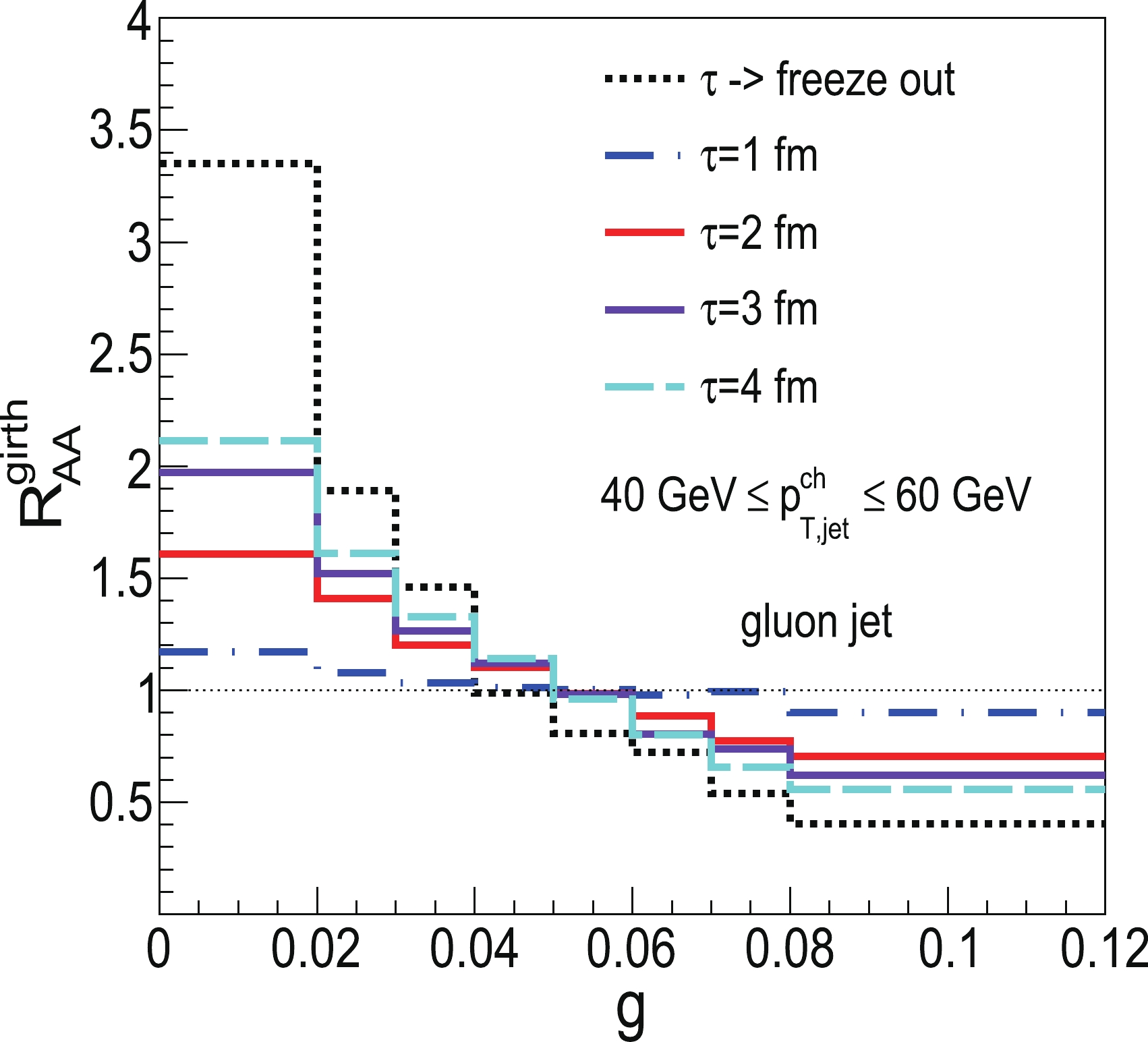
Figure 4. (color online) Extended jet transverse profile of quark (top panel) and gluon (bottom panel) jets in p+p collisions at
$\sqrt{s}=2.76$ TeV.For normalized quark (gluon) jet girth distributions, to understand why
$ R_{AA}^{\rm girth} >1 $ in small g regions and$ R_{AA}^{\rm girth} <1 $ in large g regions, as shown in Fig. 3, we turn to another very closely related jet substructure observable of girth: jet shape (or jet profile) [21, 24-26]. In fact, girth gives the first radial moment of jet shape [51]. Jet shape characterizes the averaged transverse momentum profile of a jet in$ \Delta r $ , which is defined as$ \rho(r) = \frac{1}{\Delta{r}}\frac{1}{N_{\rm jet}}\sum\limits_{\rm jet}\frac{\sum_{i}p_{T,\rm jet}^{i}(r-\Delta{r}/2,r+\Delta{r}/2)}{p_{T,\rm jet}(0,R)}, $

(5) where r is the distance to the jet axis inside the jet.
$ p_{T,\rm jet}^{i} $ is the transverse momentum of the ith constituents inside jets. It is noted that, in our model, all the showered partons should lose energy when they traverse the QGP due to the jet quenching effect. After they traverse through the QGP and hadronization occurs, the hadrons fragmented from the less energetic parton may fall off the kinematic cut of the jet candidate. In contrast, medium induced gluon radiation will provide additional particles in the event list.Figure 5 presents the transverse momentum distributions of quark and gluon jets inside a jet cone calculated from jet constituents by four
$ p_{T} $ bins. We find that the constituents with the highest$ p_{T} $ are more likely to be distributed closely to the jet axis for both quark and gluon jets. We plot the nuclear modification factor of jet shape$ R_{AA}^{\rho} = \rho_{AA}/\rho_{pp} $ in Fig. 6. It can be easily observed that distributions of particles with low$ p_T $ are enhanced in Pb+Pb relative to those in p+p, whereas distributions of particles with very large$ p_T $ are suppressed, which holds true for both gluon and quark jets. The enhanced distribution of soft fragments inside a jet can lead to$ R_{AA}^{\rm girth} >1 $ at small girths for both gluon and quark jets.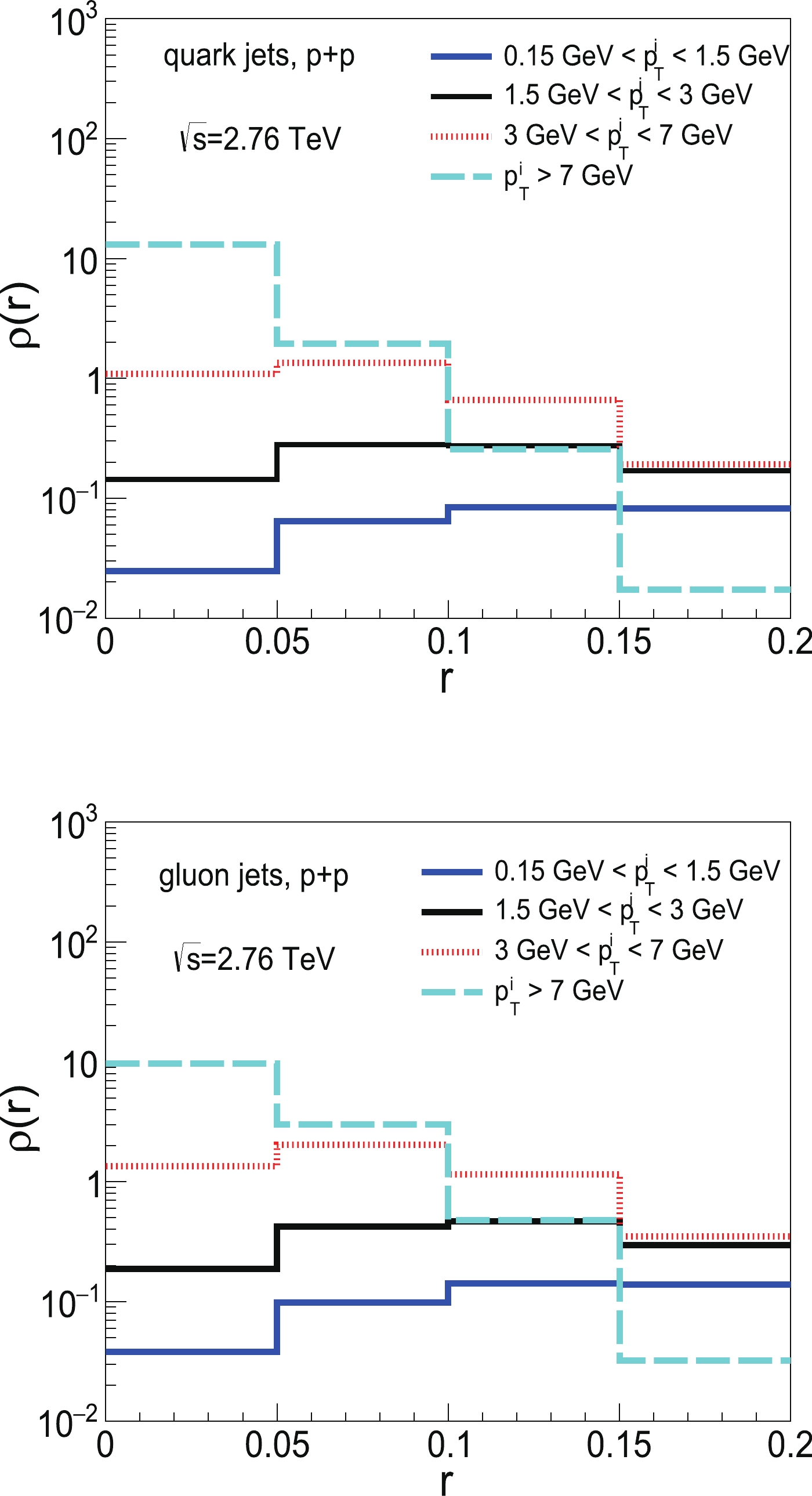
Figure 5. (color online) Extended jet transverse profile of quark (top panel) and gluon (bottom panel) jets in p+p collisions at
$\sqrt{s}=2.76$ TeV.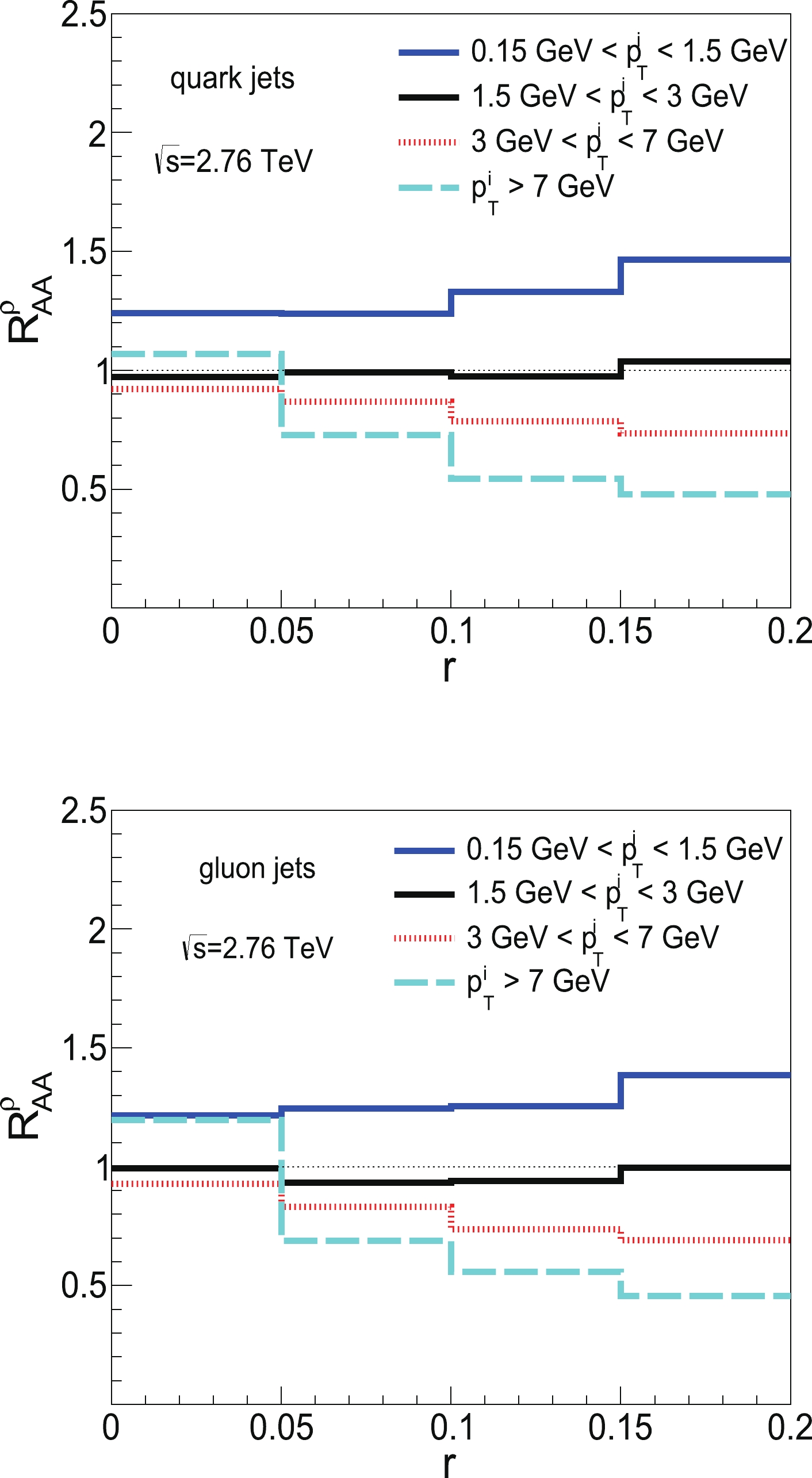
Figure 6. (color online) Nuclear modification ratio of extended jet transverse profile of quark (top panel) and gluon (bottom panel) jets in Pb+Pb to that in p+p collisions at
$\sqrt{s}=2.76$ TeV.To see the impact of different medium modifications of girth distributions for gluon and quark jets, we also calculate the event normalized distribution of girth of
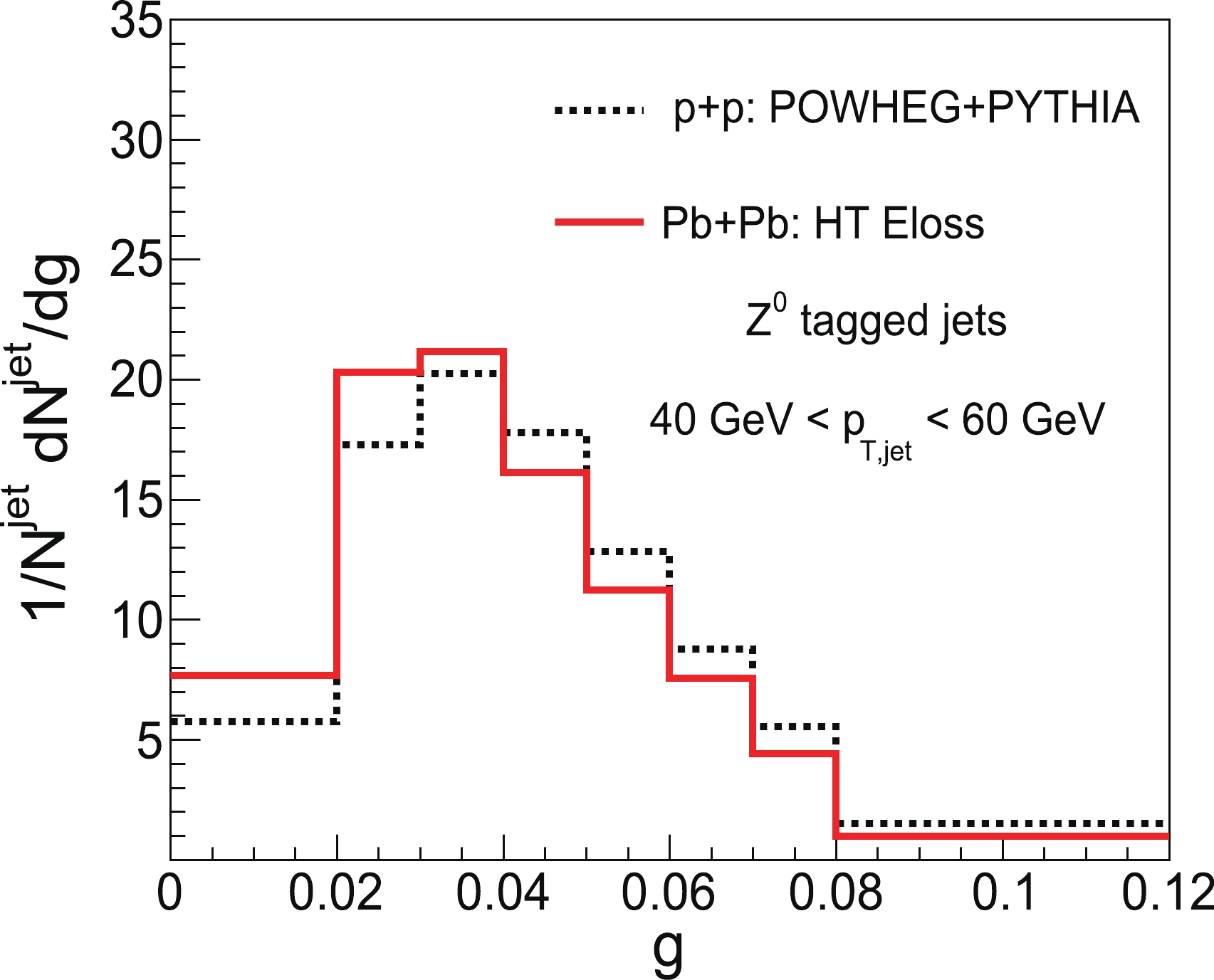
$ Z^0 $ tagged jets, which are dominated by quark jets both in p+p and Pb+Pb collisions. We adopt the same kinematic cuts as those in the CMS experiment [23] to select$ Z^0 $ tagged jet events in both p+p and Pb+Pb collisions. Two decay channels are taken into account during the reconstruction of the massive gauge boson$ Z^0 $ :$ Z^0\rightarrow e^+e^- $ and$ Z^0 \rightarrow \mu^+\mu^- $ . We choose events in which electrons have$ p_{T}^{e}>20 $ GeV and$ |\eta^{e}|<2.5 $ , whereas muons have$ p_{T}^{\mu}>10 $ GeV and$ |\eta^{\mu}|<2.4 $ . The$ Z^0 $ bosons are then reconstructed by lepton pairs with mass$ 70 \ {\rm GeV}<M_{ll}<110 $ GeV and$ p_{T}^{Z}>40 $ GeV. Jets are constructed by FASTJET from final-state charged hadrons with the anti-$ k_T $ algorithm and jet radius$ R = 0.2 $ . All the jets tagged with$ Z^0 $ are required to pass the threshold$ p_{T,\rm jet}>30 $ GeV and are rejected in the radius of$ R <0.4 $ from a lepton to suppress jet energy contamination. Jets are further chosen to have$ 40 \ {\rm GeV} <p_{T, \rm jet}<60 $ GeV and$ \left| \eta_{\rm jet} \right|<0.7 $ .The normalized distributions of girth for
$ Z^0 $ tagged jets in p+p and Pb+Pb collisions at$ \sqrt{s} = 2.76 $ TeV are plotted in Fig. 7. Compared to those in p+p collisions, the girth distributions in Pb+Pb collisions are also shifted to lower g regions, as observed for the girth distributions for inclusive jets. We further calculate the nuclear modification ratio of girth distributions for$ Z^0 $ tagged jets, as shown in Fig. 8. The nuclear modifications of girth distributions for inclusive jets are much stronger than those for$ Z^0 $ tagged jets. This distinction is largely attributed to the flavor composition of$ Z^0 $ tagged jets and inclusive jets. As summarized in Table 1,$ Z^0 $ tagged jets are dominated by quark jets, whereas inclusive jets have a more significant fraction of gluon jets. Because nuclear modifications of girth distributions for gluon jets are larger than those for quark jets (see, for example, Fig. 3), the nuclear modifications of girth distributions for$ Z^0 $ tagged jets should be weaker compared with those for inclusive jets.quark jet fraction p+p Pb+Pb inclusive jets 33% 45% $Z^0$ tagged jets

88% 92% Table 1. Estimation of quark jet fraction of inclusive jets and
$Z^0$ tagged jets in p+p and Pb+Pb collisions at leading-order (LO), with jet radius$R=0.2$ and$40 \ {\rm GeV} < p_{T,\rm jet} < 60$ GeV. -
In this paper, with an NLO+PS event generator POWHEG+PYTHIA for p+p baseline and HT parton energy loss formalism for jet quenching, we have studied the nuclear modifications of girth distributions for both inclusive jets and
$ Z^0 $ tagged jets with a small radius$ R = 0.2 $ in Pb+Pb collisions at$ \sqrt{s} = 2.76 $ TeV. Our numerical results of inclusive jets provide reasonable descriptions of ALICE data. We show that girth distributions for inclusive jets are shifted to lower girth regions in Pb+Pb collisions compared to those in p+p collisions, and similar trends have also been observed for quark and gluon jets. We find two factors contributing to the nuclear modifications of girth distributions: softer fragments inside a jet (inclusive jets, i.e., quark jets and gluon jets) after jet-medium interaction and the enhanced fraction of quark-initiated jets in HIC. Girth distributions for gluon jets show stronger nuclear modifications than those for quark jets in HIC, as gluons may suffer more energy loss than quarks in our model. We further give a prediction of girth distributions for$ Z^0 $ boson tagged jets in both p+p and Pb+Pb collisions at$ \sqrt{s} = 2.76 $ TeV. The medium modification of girth distributions for$ Z^0 $ tagged jets is found to be less pronounced compared to that for inclusive jets, as$ Z^0 $ tagged jets are dominated by quark-initiated jets. -
The authors would like to thank G Y Ma, S L Zhang, S Wang, and Q Zhang for helpful discussions.
Medium modifications of girth distributions for inclusive jets and Z0+jets in relativistic heavy-ion collisions at the LHC
- Received Date: 2020-05-05
- Available Online: 2021-02-15
Abstract: In this paper, we investigate the medium modifications of girth distributions for inclusive jets and






 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF


















 DownLoad:
DownLoad: