-
Recently, the CMS collaboration observed a broad excess of events in the region of
$ 6040-6100\,{\rm{MeV}} $ in the$ \Lambda_b^0\pi^+\pi^- $ invariant mass spectrum based on a data sample corresponding to an integrated luminosity of up to$ 140\, {\rm{fb}}^{-1} $ [1]. If it is fitted with a single Breit-Wigner function, the obtained mass and width are$ M = 6073\pm 5\,{\rm{MeV}} $ and$ \Gamma = 55 \pm 11\,{\rm{MeV}} $ , respectively. Subsequently, the LHCb collaboration observed a new excited baryon state in the$ \Lambda_b^0\pi^+\pi^- $ invariant mass spectrum with high significance using a data sample corresponding to an integrated luminosity of$ 9\,{{\rm{fb}}}^{-1} $ . The measured mass and natural width are$ M = 6072.3\pm 2.9\pm 0.6\pm 0.2\,{\rm{MeV}} $ and$\Gamma = 72\pm 11\pm 2\,{\rm{MeV}}$ , respectively, which are consistent with the first radial excitation of the$ \Lambda_b^0 $ baryon, the$\Lambda_b^0({{2S}})$ resonance [2].$ \Lambda_b(6072) $ can be assigned to be the$\Lambda_b^0({{2S}})$ state [3, 4], or assigned to be the lowest$ \rho $ -mode excitation in the$ \Lambda_b $ family [5].In 2001, at the charm sector, the CLEO collaboration observed
$ \Lambda_c^+(2765) $ or$ \Sigma_c^+(2765) $ in the$ \Lambda_c^+ \pi^- \pi^+ $ invariant mass spectrum using a$ 13.7 {\rm{fb}}^{-1} $ data sample recorded by the CLEO detector at CESR [6]. The Belle collaboration determined the isospin of$ \Lambda_c^+(2765) $ or$ \Sigma_c^+(2765) $ to be zero using a$ 980{\rm{fb}}^{-1} $ data sample in the$ e^+ e^- $ annihilation around$ \sqrt{s} = 10.6\,{\rm{GeV}} $ , and established it to be a$ \Lambda_c $ resonance [7].$ \Lambda_c(2765) $ can be assigned to be the$\Lambda_c({{2S}})$ state [8, 9]; however, there are several other possible assignments [10].In 2006, the Belle collaboration reported the first observation of two charmed strange baryon states that decay into the final state
$ \Lambda_c^+ K^-\pi^+ $ ; the broader one has a mass of$ 2978.5\pm 2.1\pm 2.0\, {\rm{MeV}} $ and a width of$43.5\pm 7.5\pm 7.0 \,{\rm{MeV}}$ [11]. Subsequently, the BaBar collaboration confirmed$ \Xi_c(2980) $ or$ \Xi_c(2970) $ [12].$ \Xi_c(2980/2970) $ can be assigned to be the$\Xi_c({{2S}})$ state [8, 9]; however, there are several other possible assignments [10].The mass spectrum of the single heavy baryon states has been studied intensively in various theoretical models [3-38]. If
$ \Lambda_b(6072) $ ,$ \Lambda_c(2765) $ and$ \Xi_c(2980) $ are the first radial excited states of$ \Lambda_b $ ,$ \Lambda_c $ and$ \Xi_c $ , respectively, the mass gaps between the ground states and first radial excited states are less than$ 0.5\,{\rm{GeV}} $ , which are significantly lower than the amount that is expected by the 3-dimensional harmonic oscillator model. In the QCD sum rules for the single heavy baryon states, if we carry out the operator product expansion up to the vacuum condensates of dimension 6, we have to choose the continuum threshold parameters as$ \sqrt{s_0} = M_{gr}+0.6\sim0.8\,{\rm{GeV}} $ or$ 0.7\sim 0.9\,{\rm{GeV}} $ to reproduce the experimental data [26-32], where the subscript$ gr $ stands for the ground states. The energy gaps$ 0.6\sim0.8\,{\rm{GeV}} $ and$ 0.7\sim0.9\,{\rm{GeV}} $ are much larger than the physical energy gap$ 0.5\,{\rm{GeV}} $ , in which the contributions of the first radial excited states are included. The heavy baryon states, which have one heavy quark and two light quarks, play an important role in understanding the dynamics of light quarks in the presence of one heavy quark, and also in understanding the confinement mechanism and heavy quark symmetry.At the hadron side of the correlation functions in the QCD sum rules for the heavy baryon states, there are one heavy and two light quark propagators. If the heavy quark line emits a gluon, each light quark line contributes a quark-antiquark pair, and we obtain quark-gluon operators of dimension 10. In previous works, the operator product expansion was carried out up to vacuum condensates of dimension 6 [22-32]. In Ref. [29], we study the masses and pole residues of the
${1\over 2}^\pm$ flavor antitriplet heavy baryon states ($ \Lambda_c^+ $ ,$ \Xi_c^+,\Xi_c^0) $ and ($ \Lambda_b^0 $ ,$ \Xi_b^0,\Xi_b^-) $ by subtracting the contributions from the corresponding$ {1\over 2}^\mp $ heavy baryon states with the QCD sum rules. Herein, we revisit our previous work by calculating the vacuum condensates up to dimension 10, extend our previous work to study the first radial excited states$\Lambda_Q({{2S}})$ and$\Xi_Q({{2S}})$ , and make possible assignments of$ \Lambda_b(6072) $ ,$ \Lambda_c(2765) $ and$ \Xi_c(2980) $ .The article is arranged as follows: we derive the QCD sum rules for the masses and pole residues of the heavy baryon states
$\Lambda_Q({{1S}},{{2S}})$ and$\Xi_Q({{1S}},{{2S}})$ in Sec. II; in Sec. III, we present the numerical results and discussions; and Sec. IV is reserved for our conclusions. -
We interpolate the spin-parity
$ J^P = {1\over 2}^+ $ flavor antitriplet heavy baryon states$ \Lambda_Q $ ,$\Lambda_Q({{2S}})$ ,$ \Xi_Q $ , and$\Xi_Q({{2S}})$ with the$ \Lambda $ -type currents$ J_\Lambda(x) $ and$ J_\Xi(x) $ , respectively,$ \begin{aligned}[b] J_\Lambda(x) = \varepsilon^{ijk} u^T_i(x)C\gamma_5 d_j(x) Q_k(x) \, , \\ J_\Xi(x)= \varepsilon^{ijk} q^T_i(x)C\gamma_5 s_j(x) Q_k(x) \, , \end{aligned} $

(1) where
$ Q = c $ , b;$ q = u $ , d; i, j, and k are color indexes; and C is the charge conjunction matrix.The attractive interaction induced by one-gluon exchange favors forming diquark states or quark-quark-correlations in the color antitriplet
$ \overline{3}_{ c} $ [39, 40]. The color antitriplet diquark operators$ \varepsilon^{ijk} q^{T}_j C\Gamma q^{\prime}_k $ have five structures in the Dirac spinor space, where$ C\Gamma = C\gamma_5 $ , C,$ C\gamma_\mu \gamma_5 $ ,$ C\gamma_\mu $ , and$ C\sigma_{\mu\nu} $ for the scalar, pseudoscalar, vector, axialvector, and tensor diquarks, respectively, and couple potentially to the corresponding scalar, pseudoscalar, vector, axialvector, and tensor diquark states, respectively. The calculations via the QCD sum rules indicate that the favored quark-quark configurations are the scalar and axialvector diquark states, while the most favored quark-quark configurations are the scalar diquark states [41]. We usually resort to the light-diquark-heavy-quark model to study the heavy baryon states. In the diquark-quark models, the angular momentum between the two light quarks is denoted as$ L_\rho $ , while the angular momentum between the light diquark and the heavy quark is denoted as$ L_\lambda $ . If the two light quarks in the diquark are in relative S-wave or$ L_\rho = 0 $ , then the heavy baryon states with the spin-parity$ J^P = 0^+ $ and$ 1^+ $ diquark constituents are called$ \Lambda $ -type and$ \Sigma $ -type baryons, respectively [42]. In this article, we study the ground states and first radial excited states of$ \Lambda $ -type heavy baryons with$ \Lambda $ -type interpolating currents.We can interpolate the corresponding spin-parity
$ J^P = {1\over 2}^- $ flavor antitriplet heavy baryon states with the$ \Lambda $ -type currents$ i \gamma_{5}J_\Lambda(x) $ and$ i \gamma_{5}J_\Xi(x) $ without introducing the relative P-wave explicitly, because multiplying$ i \gamma_{5} $ with the currents$ J_\Lambda(x) $ and$ J_\Xi(x) $ changes their parity [43]. We now write the correlation functions,$\ \Pi(p) = {\rm i}\int {\rm d}^4x {\rm e}^{{\rm i}p \cdot x} \langle0|T\Big\{J(x)\bar{J}(0)\Big\}|0\rangle \, , $

(2) where
$ J(x) = J_\Lambda(x) $ and$ J_\Xi(x) $ .We insert a complete set of intermediate baryon states with the same quantum numbers as the current operators
$ J_\Lambda(x) $ ,$ i \gamma_{5}J_\Lambda(x) $ ,$ J_\Xi(x) $ and$ i \gamma_{5}J_\Xi(x) $ into the correlation functions$ \Pi(p) $ to obtain the hadronic representation [44-46]. After isolating the pole terms of the ground states and the first radial excited states, we obtain the following results:$ \begin{aligned}[b]\Pi(p) = & \lambda_+^2 {\not\!\!{p} + M_{+} \over M^{2}_+ -p^{2} } + \lambda_{{{2S}},+}^2 {\not\!\!{p} + M_{{{2S}},+} \over M^{2}_{{{2S}},+} -p^{2} } \\ & +\lambda_{-}^2 {\not\!\!{p} - M_{-} \over M_{-}^{2}-p^{2} }+\lambda_{{{2S}},-}^2 {\not\!\!{p} - M_{{{2S}},-} \over M_{{{2S}},-}^{2}-p^{2} } +\cdots \, , \end{aligned} $

(3) where
$ M_{\pm} $ and$M_{{{2S}},\pm}$ are the masses of the ground states and first radial excited states with the parity$ \pm $ respectively, and$ \lambda_{\pm} $ and$\lambda_{{{2S}},\pm}$ are the corresponding pole residues defined by$\langle 0|J(0)|B_{\pm/{{2S}},\pm}(p)\rangle = \lambda_{\pm/{{2S}},\pm}$ ,$ B = \Lambda_Q $ and$ \Xi_Q $ .We rewrite the correlation functions as
$ \Pi(p) = \not\!\!{p}\, \Pi_{1}(p^2) + \Pi_{0}(p^2)\, , $

(4) according to the Lorentz covariance, and obtain the hadronic spectral densities through the dispersion relation
$ \begin{aligned}[b]\rho_{H,1}(s) =&{\rm{lim}}_{\epsilon \to 0}\frac{{\rm{Im}}\Pi_1(s+i\epsilon) }{\pi}\, , \\ = &\lambda_+^2 \delta\left(s- M^{2}_+\right) + \lambda_{{{2S}},+}^2\delta\left(s- M^{2}_{{{2S}},+} \right) \\ &+ \lambda_{-}^2 \delta\left(s- M^{2}_{-}\right) + \lambda_{{{2S}},-}^2\delta\left(s- M^{2}_{{{2S}},-} \right) + \cdots \, , \end{aligned} $

(5) $ \begin{aligned}[b]\rho_{H,0}(s) =& {\rm{lim}}_{\epsilon \to 0}\frac{{\rm{Im}}\Pi_0(s+i\epsilon) }{\pi}\, ,\\ = & M_+\lambda_+^2 \delta\left(s- M^{2}_+\right) \\ &+ M_{{{2S}},+}\lambda_{{{2S}},+}^2\delta\left(s- M^{2}_{{{2S}},+} \right) -M_{-}\lambda_{-}^2 \delta\left(s- M^{2}_{-}\right) \\ &- M_{{{2S}},-} \lambda_{{{2S}},-}^2\delta\left(s- M^{2}_{{{2S}},-} \right)+ \cdots \, , \end{aligned} $

(6) where we add the subscript H to denote the hadron side of the correlation functions.
We now carry out the operator product expansion up to the vacuum condensates of dimension 10 in a consistent way, and consider the vacuum condensates, which are quark-gluon operators of the order
$ \mathcal{O}(\alpha_s^k) $ with$ k\leq1 $ . Again, we obtain the corresponding QCD spectral densities through the dispersion relation$ \begin{aligned}[b]\rho_{{\rm QCD},1}(s)& ={\rm{lim}}_{\epsilon \to 0}\frac{{\rm{Im}}\Pi_1(s+i\epsilon) }{\pi}\, , \\ \rho_{{\rm QCD},0}(s)& = {\rm{lim}}_{\epsilon \to 0}\frac{{\rm{Im}}\Pi_0(s+i\epsilon) }{\pi}\, , \end{aligned} $

(7) where we add the subscripts
${\rm QCD}$ to denote the QCD side of the correlation functions.Then, we choose the continuum thresholds
$ s_0 $ and$ s_0^\prime $ to include the ground states and the ground states plus first radial excited states, respectively, and introduce the weight function$\exp\left(-{s}/{T^2}\right)$ to suppress the contributions of the higher resonances and continuum states. We take the combination$ \int_{m_Q^2}^{s_0/s_0^\prime}{\rm d}s \Big[\sqrt{s}\rho_{H,1}(s)+\rho_{H,0}(s)\Big]\exp\left(-\frac{s}{T^2}\right)\, , $

(8) to exclude the contaminations from the heavy baryon states with negative parity, and match the hadron side with the QCD side of the correlation functions. The combinations
$ \int_{m_Q^2}^{\infty}{\rm d}s \Big[\sqrt{s}\rho_{H,1}(s)\pm\rho_{H,0}(s)\Big]\exp\left(-\frac{s}{T^2}\right)\, ,$

(9) pick up the heavy baryon states with positive and negative parities, respectively.
Finally, we obtain two QCD sum rules:
$ \begin{aligned}[b] 2M_{+}\lambda_{+}^2\exp\left(-\frac{M_{+}^2}{T^2}\right) =& \int_{m_Q^2}^{s_0}{\rm d}s \Big[\sqrt{s}\rho_{H,1}(s) +\rho_{H,0}(s)\Big]\exp\left(-\frac{s}{T^2}\right) \, = \int_{m_Q^2}^{s_0}{\rm d}s \Big[\sqrt{s}\rho_{{\rm QCD},1}(s) + \rho_{{\rm QCD},0}(s)\Big]\exp\left(-\frac{s}{T^2}\right) \, , \end{aligned} $

(10) $ \begin{aligned}[b] 2M_{+} \lambda_{+}^2\exp\left(-\frac{M_{+}^2}{T^2}\right)+2M_{{{2S}},+}\lambda_{{{2S}},+}^2\exp\left(-\frac{M_{{{2S}},+}^2}{T^2}\right) = & \int_{m_Q^2}^{s_0^\prime}{\rm d}s \Big[\sqrt{s}\rho_{H,1}(s)+\rho_{H,0}(s)\Big]\exp\left(-\frac{s}{T^2}\right) \, ,\\ =&\int_{m_Q^2}^{s_0^\prime}{\rm d}s \Big[\sqrt{s}\rho_{\rm QCD,1}(s)+\rho_{\rm QCD,0}(s)\Big]\exp\left(-\frac{s}{T^2}\right) \, , \end{aligned} $

(11) where
$\rho_{\rm QCD,1}(s) = \rho_{\Lambda,1}(s)$ ,$ \rho_{\Xi,1}(s) $ ,$\rho_{\rm QCD,0}(s) = m_Q\,\rho_{\Lambda,0}(s)$ ,$ m_Q\,\rho_{\Xi,0}(s) $ ,$ \begin{aligned}[b] \rho_{\Lambda,1}(s)& = \rho_{\Xi,1}(s)\mid_{m_s\to 0,\, \langle\bar{s}s\rangle\to\langle\bar{q}q\rangle, \,\langle\bar{s}g_s\sigma Gs\rangle\to\langle\bar{q}g_s\sigma Gq\rangle }\, , \\ \rho_{\Lambda,0}(s)& =\rho_{\Xi,0}(s)\mid_{m_s\to 0, \, \langle\bar{s}s\rangle\to\langle\bar{q}q\rangle, \,\langle\bar{s}g_s\sigma Gs\rangle\to\langle\bar{q}g_s\sigma Gq\rangle }\, , \end{aligned} $

(12) $ \begin{aligned}[b]\rho_{\Xi,1}(s) = & \dfrac{3}{128\pi^4}\int_{x_i}^1{\rm d}x \,x(1-x)^2(s-\widetilde{m}_Q^2)^2 +\dfrac{ m_s [\langle \bar{s}s\rangle-2\langle \bar{q}q\rangle]}{32\pi^2}\left(1-x_i^2 \right) -\dfrac{m_s[\langle \bar{s}g_s\sigma Gs\rangle-3\langle \bar{q}g_s\sigma Gq\rangle]}{96\pi^2}\delta (s-m_Q^2) \\ & +\dfrac{\langle \bar{s}s\rangle\langle \bar{q}q\rangle}{6}\delta (s-m_Q^2) -\dfrac{[\langle \bar{s}s\rangle\langle \bar{q}g_s\sigma Gq\rangle+\langle \bar{s}g_s\sigma Gs\rangle\langle \bar{q}q\rangle]}{24 T^2} \left(1+\dfrac{s}{T^2} \right)\delta (s-m_Q^2) \\ &+\dfrac{m_Q^4\langle \bar{q}g_s\sigma Gq\rangle\langle \bar{s}g_s\sigma Gs\rangle}{96 T^8}\delta (s-m_Q^2) +\dfrac{1}{256\pi^2}\langle\dfrac{\alpha_{s}GG}{\pi}\rangle\left(1-x_i^2 \right)\\ & -\dfrac{m_{Q}^{2}}{384\pi^2} \langle\dfrac{\alpha_{s}GG}{\pi}\rangle \int_{x_{i}}^{1}{\rm d}x\, \dfrac{(1-x)^2}{x^2} -\dfrac{m_sm_Q^2[\langle \bar{s}s\rangle-2\langle \bar{q}q\rangle]}{288T^4}\langle\dfrac{\alpha_{s}GG}{\pi}\rangle \dfrac{1-x_i}{x_i}\\ &-\dfrac{m_Q^2\langle \bar{s} s\rangle\langle \bar{q}q\rangle\pi^2}{108T^6}\langle\dfrac{\alpha_{s}GG}{\pi}\rangle\delta (s-m_Q^2)\, , \end{aligned} $

(13) $ \begin{aligned}[b]\rho_{\Xi,0}(s) =&\dfrac{3}{128\pi^4}\int_{x_i}^1{\rm d}x \,(1-x)^2(s-\widetilde{m}_Q^2)^2 +\dfrac{ m_s [\langle \bar{s}s\rangle-2\langle \bar{q}q\rangle]}{16\pi^2}\left(1-x_i \right)-\dfrac{m_s[\langle \bar{s}g_s\sigma Gs\rangle-3\langle \bar{q}g_s\sigma Gq\rangle]}{96\pi^2}\delta (s-m_Q^2) \\ &+\dfrac{\langle \bar{s}s\rangle\langle \bar{q}q\rangle}{6}\delta (s-m_Q^2) -\dfrac{m_Q^2[\langle \bar{s}s\rangle\langle \bar{q}g_s\sigma Gq\rangle+\langle \bar{s}g_s\sigma Gs\rangle\langle \bar{q}q\rangle]}{24 T^2} \delta (s-m_Q^2) +\dfrac{m_Q^2\langle \bar{q}g_s\sigma Gq\rangle\langle \bar{s}g_s\sigma Gs\rangle}{48 T^6}\left(-1+\frac{s}{2T^2} \right) \delta (s-m_Q^2) \\ &-\dfrac{m_{Q}^{2}}{384\pi^2} \langle\dfrac{\alpha_{s}GG}{\pi}\rangle \int_{x_{i}}^{1}{\rm d}x\, \dfrac{(1-x)^2}{x^3}+\dfrac{1}{128\pi^2}\langle\dfrac{\alpha_{s}GG}{\pi}\rangle\int_{x_{i}}^{1}{\rm d}x\,\dfrac{(1-x)^2}{x^2}+\dfrac{1}{128\pi^2}\langle\dfrac{\alpha_{s}GG}{\pi}\rangle\left(1-x_i \right)\\ &-\dfrac{m_sm_Q^2[\langle \bar{s}s\rangle-2\langle \bar{q}q\rangle]}{576T^4}\langle\dfrac{\alpha_{s}GG}{\pi}\rangle \,\dfrac{1-x_i^2}{x_i^2}+\dfrac{ m_s [\langle \bar{s}s\rangle-2\langle \bar{q}q\rangle]}{96T^2}\langle\dfrac{\alpha_{s}GG}{\pi}\rangle\dfrac{1-x_i}{x_i} \\ &-\dfrac{m_Q^2\langle \bar{s} s\rangle\langle \bar{q}q\rangle\pi^2}{108T^6}\langle\dfrac{\alpha_{s}GG}{\pi}\rangle\delta (s-m_Q^2)+\dfrac{\langle \bar{s} s\rangle\langle \bar{q}q\rangle\pi^2}{36T^4}\langle\dfrac{\alpha_{s}GG}{\pi}\rangle\delta (s-m_Q^2)\, , \end{aligned} $

(14) $x_i = \dfrac{m_Q^2}{s}$ , where$ T^2 $ is the Borel parameter.We derive the QCD sum rules in Eq. (10) with regard to
${1}/{T^2}$ , and then eliminate the pole residues$ \lambda_{+} $ and obtain the masses of the ground states$ \Lambda_Q $ and$ \Xi_Q $ ,$ M_{+}^2=\dfrac{-\dfrac{\rm d}{{\rm d}(1/T^2)}\displaystyle\int_{m_Q^2}^{s_0}{\rm d}s \Big[\sqrt{s}\rho_{\rm QCD,1}(s)+\rho_{\rm QCD,0}(s)\Big]\exp\left(-\dfrac{s}{T^2}\right)}{\displaystyle\int_{m_Q^2}^{s_0}{\rm d}s \Big[\sqrt{s}\rho_{\rm QCD,1}(s)+\rho_{\rm QCD,0}(s)\Big]\exp\left(-\dfrac{s}{T^2}\right)}\, . $

(15) Hereafter, we will refer to the QCD sum rules in Eq. (10) and Eq. (15) as QCDSR I.
We introduce the notations
$\tau = {1}/{T^2}$ ,$D^n = \left( - {\rm d}/{{\rm d}\tau}\right)^n$ , and use the subscripts$ 1 $ and$ 2 $ to represent the ground states$ \Lambda_Q $ ,$ \Xi_Q $ , and the first radially excited states$\Lambda_Q({{2S}})$ ,$\Xi_Q({{2S}})$ , respectively, for simplicity.$ \tilde{\lambda}_1^2\exp\left(-\tau M_1^2 \right)+\tilde{\lambda}_2^2\exp\left(-\tau M_2^2 \right)=\Pi^{\prime}_{\rm QCD}(\tau) \, , $

(16) where
$ \tilde{\lambda}_1^2 = 2M_{+}\lambda_{+}^2 $ ,$ \tilde{\lambda}_2^2 = 2M_{{\rm{2S}},+}\lambda_{{\rm{2S}},+}^2 $ , we introduce the subscript${\rm QCD}$ to denote the QCD representation of the correlation functions below the continuum thresholds$ s_0^\prime $ . Firstly, let us derive the QCD sum rules in Eq. (16) with respect to$ \tau $ to obtain$ \tilde{\lambda}_1^2M_1^2\exp\left(-\tau M_1^2 \right)+\tilde{\lambda}_2^2M_2^2\exp\left(-\tau M_2^2 \right) = D\Pi^{\prime}_{\rm QCD}(\tau) \, . $

(17) From Eqs. (16)-(17), we can obtain the QCD sum rules
$ \tilde{\lambda}_i^2\exp\left(-\tau M_i^2 \right)=\dfrac{\left(D-M_j^2\right)\Pi^{\prime}_{\rm QCD}(\tau)}{M_i^2-M_j^2} \, , $

(18) where the sub-indexes
$ i \neq j $ . We can then derive the QCD sum rules in Eq. (18) with respect to$ \tau $ to obtain$ \begin{aligned}[b]M_i^2& =\dfrac{\left(D^2-M_j^2D\right)\Pi_{\rm QCD}^{\prime}(\tau)}{\left(D-M_j^2\right)\Pi_{\rm QCD}^{\prime}(\tau)} \, , \\ M_i^4& =\dfrac{\left(D^3-M_j^2D^2\right)\Pi_{\rm QCD}^{\prime}(\tau)}{\left(D-M_j^2\right)\Pi_{\rm QCD}^{\prime}(\tau)}\, . \end{aligned} $

(19) The squared masses
$ M_i^2 $ satisfy the equation$ M_i^4-b M_i^2+c=0\, ,$

(20) where
$ \begin{aligned}[b]b& =\dfrac{D^3\otimes D^0-D^2\otimes D}{D^2\otimes D^0-D\otimes D}\, , \\ c & =\dfrac{D^3\otimes D-D^2\otimes D^2}{D^2\otimes D^0-D\otimes D}\, , \\ D^j \otimes D^k & = D^j\Pi^{\prime}_{\rm QCD}(\tau) \, D^k\Pi^{\prime}_{\rm QCD}(\tau)\, , \end{aligned} $

(21) with the indexes
$ i = 1,2 $ and$ j,k = 0,1,2,3 $ . Finally, we solve the equation in Eq. (20) analytically to obtain two solutions [47-49],$ M_1^2 =\dfrac{b-\sqrt{b^2-4c} }{2} \, , $

(22) $ M_2^2 =\dfrac{b+\sqrt{b^2-4c} }{2} \, . $

(23) From the QCD sum rules in Eqs. (22)-(23), we can obtain both the masses of the ground states and the first radial excited states. The ground state masses from the QCD sum rules in Eq. (22) suffer from additional uncertainties from the first radial excited states
$\Lambda_Q({{2S}})$ and$\Xi_Q({{2S}})$ , and we neglect the QCD sum rules in Eq. (22). Hereafter, we will refer to the QCD sum rules in Eq. (18) and Eq. (23) as QCDSR II. -
At the QCD side, we take the vacuum condensates to be the standard values
$ \langle\bar{q}q \rangle = -(0.24\pm 0.01\, {\rm{GeV}})^3 $ ,$\langle\bar{s}s \rangle = (0.8\pm0.1)\langle\bar{q}q \rangle$ ,$ \langle\bar{q}g_s\sigma G q \rangle = m_0^2\langle \bar{q}q \rangle $ ,$ \langle\bar{s}g_s\sigma G s \rangle = m_0^2\langle \bar{s}s \rangle $ ,$ m_0^2 = (0.8 \pm 0.1)\,{\rm{GeV}}^2 $ ,$\langle \dfrac{\alpha_s GG}{\pi}\rangle = 0.012\pm0.004\,{\rm{GeV}}^4$ at the energy scale$ \mu = 1\, {\rm{GeV}} $ [44-50], and take the$ \overline{MS} $ masses$ m_{c}(m_c) = (1.275\pm0.025)\,{\rm{GeV}} $ ,$m_{b}(m_b) = (4.18\pm 0.03)\,{\rm{GeV}}$ and$ m_s(\mu = 2\,{\rm{GeV}}) = (0.095\pm0.005)\,{\rm{GeV}} $ from the Particle Data Group [51]. Moreover, we consider the energy-scale dependence of the quark condensates, mixed quark condensates, and$ \overline{MS} $ masses according to the renormalization group equation,$ \begin{aligned}[b]\langle\bar{q}q \rangle(\mu)& =\langle\bar{q}q\rangle({\rm{1}}\;{\rm{GeV}})\left[\dfrac{\alpha_{s}({\rm{1}}\;{\rm{GeV}})}{\alpha_{s}(\mu)}\right]^{\textstyle\frac{12}{33-2n_f}}\, , \\ \langle\bar{s}s \rangle(\mu)& =\langle\bar{s}s \rangle({\rm{1}}\;{\rm{GeV}})\left[\dfrac{\alpha_{s}({\rm{1}}\;{\rm{GeV}})}{\alpha_{s}(\mu)}\right]^{\textstyle\frac{12}{33-2n_f}}\, , \\ \langle\bar{q}g_s \sigma Gq \rangle(\mu)& =\langle\bar{q}g_s \sigma Gq \rangle({\rm{1}}\;{\rm{GeV}})\left[\dfrac{\alpha_{s}({\rm{1}}\;{\rm{GeV}})}{\alpha_{s}(\mu)}\right]^{\textstyle\frac{2}{33-2n_f}}\, ,\\ \langle\bar{s}g_s \sigma Gs \rangle(\mu)& =\langle\bar{s}g_s \sigma Gs \rangle({\rm{1}}\;{\rm{GeV}})\left[\dfrac{\alpha_{s}({\rm{1}}\;{\rm{GeV}})}{\alpha_{s}(\mu)}\right]^{\textstyle\frac{2}{33-2n_f}}\, ,\\ m_b(\mu)& = m_b(m_b)\left[\frac{\alpha_{s}(\mu)}{\alpha_{s}(m_b)}\right]^{\textstyle\frac{12}{33-2n_f}} \, ,\\ m_c(\mu)& = m_c(m_c)\left[\dfrac{\alpha_{s}(\mu)}{\alpha_{s}(m_c)}\right]^{\textstyle\frac{12}{33-2n_f}} \, ,\\ m_s(\mu)& = m_s({\rm 2GeV} )\left[\dfrac{\alpha_{s}(\mu)}{\alpha_{s}({\rm 2GeV})}\right]^{\textstyle\frac{12}{33-2n_f}}\, ,\\ \alpha_s(\mu)& =\!\dfrac{1}{b_0t}\left[1-\dfrac{b_1}{b_0^2}\dfrac{\log t}{t} +\dfrac{b_1^2(\log^2{t}-\log{t}-1)+b_0b_2}{b_0^4t^2}\right]\, , \end{aligned} $

(24) where
$ \begin{aligned}[b]& t = \log \dfrac{\mu^2}{\Lambda^2} ,\quad b_0 = \dfrac{33-2n_f}{12\pi}\\ &b_1 = \dfrac{153-19n_f}{24\pi^2},\quad b_2 = \dfrac{2857-\dfrac{5033}{9}n_f+\dfrac{325}{27}n_f^2}{128\pi^3} \end{aligned} $

$\Lambda = 213\,{\rm{MeV}},\;296\,{\rm{MeV}} $ , and$ 339\,{\rm{MeV}} $ for the flavors$ n_f = 5 $ ,$ 4 $ , and$ 3 $ , respectively [51, 52]. For the charmed baryon states$\Lambda_c({{1S}},{{2S}})$ and$\Xi_c({{1S}},{{2S}})$ , we choose the flavor number$ n_f = 4 $ , while for the bottom baryon states$\Lambda_b({{1S}},{{2S}})$ and$\Xi_b({{1S}},{{2S}})$ , we choose the flavor number$ n_f = 5 $ .In QCDSR I, we choose the continuum threshold parameters to be
$ \sqrt{s_0} = M_{gr}+0.50\pm0.10\,{\rm{GeV}} $ rather than$ M_{gr}+0.6\sim0.8\,{\rm{GeV}} $ or$ 0.7\sim0.9\,{\rm{GeV}} $ as a constraint to exclude contaminations from the first radial excited states [26-32], where the subscript$ gr $ denotes the ground states$ \Lambda_Q $ and$ \Xi_Q $ . Furthermore, we choose the energy scales of the QCD spectral densities in the QCD sum rules for$ \Lambda_c $ ,$ \Xi_c $ ,$ \Lambda_b $ and$ \Xi_b $ to be the typical energy scales$ \mu = 1\,{\rm{GeV}} $ ,$ 1\,{\rm{GeV}} $ ,$ 2\,{\rm{GeV}} $ , and$ 1.8\,{\rm{GeV}} $ , respectively, where we subtract$ 0.2\,{\rm{GeV}} $ from the energy scale for$ \Xi_b $ to account for the finite mass of the s-quark. After trial and error, we obtain the Borel parameters$ T^2 $ , continuum threshold parameters$ s_0 $ , pole contributions of the ground states, and perturbative contributions, which are shown explicitly in Table 1. From the table, we can see that the pole contributions are approximately 40%-60% or 40%-70%, so the pole dominance is satisfied. The perturbative contributions are larger than 50% except for$ \Lambda_b $ , although the perturbative contribution is approximately 43%-46% in that case; the contributions of the vacuum condensates of dimension 10 are tiny, and the operator product expansion is well convergent.$T^2 /{\rm{GeV} }^2$ 

$\sqrt{s_0}/{\rm{GeV} }$ 

pole (%) perturbative (%) $ \Lambda_c $ 

$ 1.4-1.8 $ 

$ 2.75\pm0.10 $ 

40-72 50-58 $ \Xi_c $ 

$ 1.7-2.1 $ 

$ 3.00\pm0.10 $ 

42-71 64-71 $ \Lambda_b $ 

$ 3.6-4.0 $ 

$ 6.10\pm0.10 $ 

41-60 43-46 $ \Xi_b $ 

$ 3.8-4.2 $ 

$ 6.30\pm0.10 $ 

40-60 51-54 $\Lambda_c({{2S} })$ 

$ 1.8-2.4 $ 

$ 3.00\pm0.10 $ 

41-74 70-80 $\Xi_c({{2S} })$ 

$ 1.8-2.4 $ 

$ 3.25\pm0.10 $ 

54-84 74-83 $\Lambda_b({{2S} })$ 

$ 4.6-5.0 $ 

$ 6.30\pm0.10 $ 

49-66 76-79 $\Xi_b({{2S} })$ 

$ 5.1-5.5 $ 

$ 6.55\pm0.10 $ 

51-66 83-85 Table 1. Borel parameters
$ T^2 $ and continuum threshold parameters$ s_0(s_0^\prime) $ for the heavy baryon states, where "pole" stands for the pole contributions from the ground states or the ground states plus first radial excited states, and "perturbative" stands for the contributions from the perturbative terms.We now consider all uncertainties of the input parameters, and obtain the values of the masses and pole residues of the ground states of the flavor antitriplet heavy baryon states
$ \Lambda_Q $ and$ \Xi_Q $ , which are shown in Figs. 1-2 and Table 2. From Table 1 and Figs. 1-2, we can see that rather flat platforms appear in the Borel windows, and the uncertainties originating from the Borel parameters are rather small. It is the first time that we have obtained very flat platforms for the heavy baryon states. From Tables 1-2, we can see that the central values have the relation$ \sqrt{s_0}-M_{gr} = (0.50-0.55)\,{\rm{GeV}} $ ; the continuum threshold parameters$ s_0 $ are large enough to consider all the ground state contributions but small enough to suppress the first radial excited state contaminations sufficiently. Furthermore, they meet our naive expectations.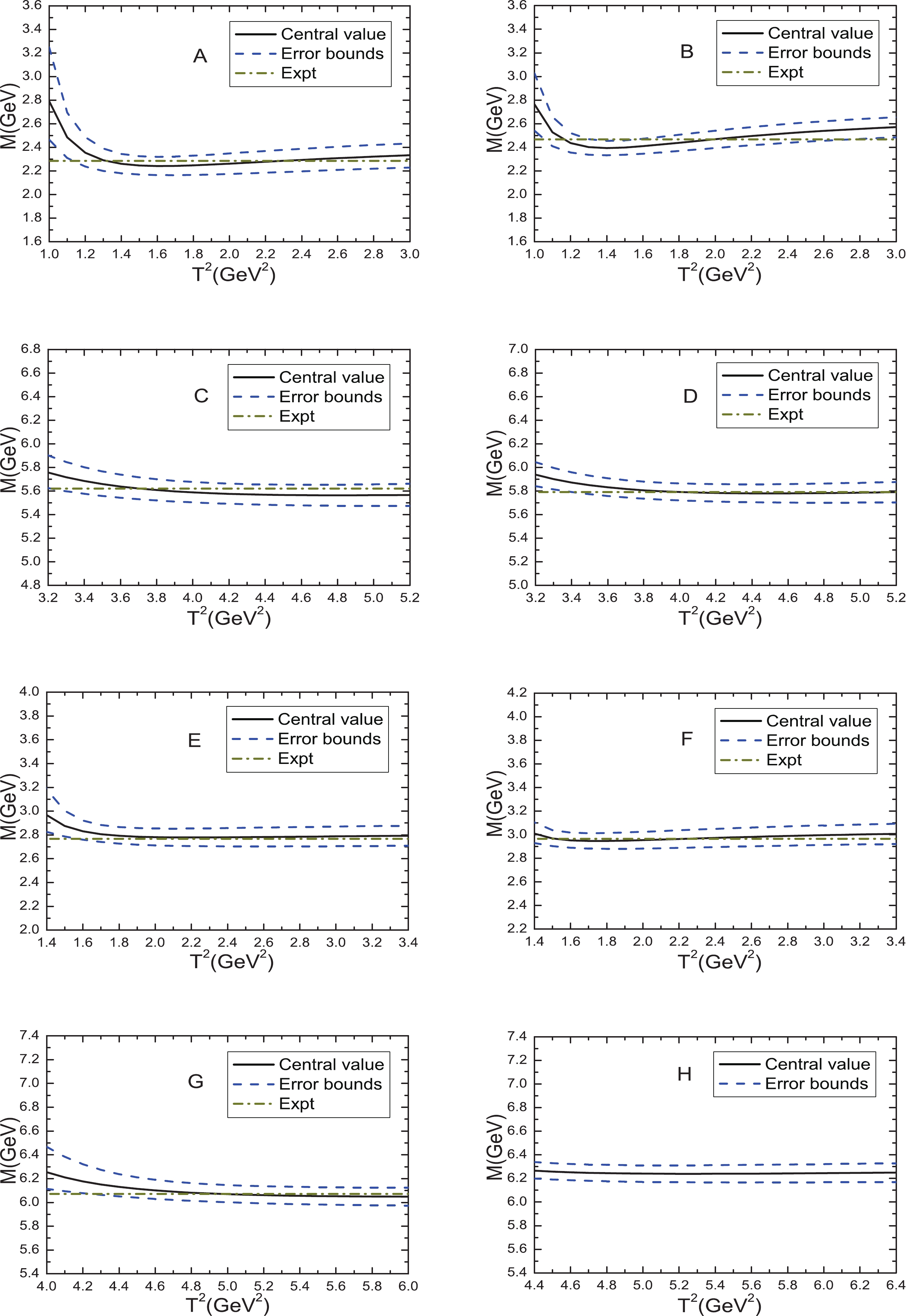
Figure 1. (color online) Masses with variations of the Borel parameters
$ T^2 $ , where A, B, C, D, E, F, G, and H correspond to$ \Lambda_c $ ,$ \Xi_c $ ,$ \Lambda_b $ ,$ \Xi_b $ ,$ \Lambda_c({{2S}}) $ ,$ \Xi_c({{2S}}) $ ,$ \Lambda_b({{2S}}) $ , and$ \Xi_b({{2S}}) $ , respectively. "Expt" denotes the experimental values.
Figure 2. (color online) Pole residues with variations of the Borel parameters
$ T^2 $ , where A, B, C, D, E, F, G, and H correspond to$ \Lambda_c $ ,$ \Xi_c $ ,$ \Lambda_b $ ,$ \Xi_b $ ,$ \Lambda_c({{2S}}) $ ,$ \Xi_c({{2S}}) $ ,$ \Lambda_b({{2S}}) $ , and$ \Xi_b({{2S}}) $ , respectively.$M/{\rm{GeV} }$ 

$\lambda(10^{-2}{\rm{GeV} }^3)$ 

$M/{\rm{GeV} }[{\rm{expt} }]$ 

$ \Lambda_c $ 

$ 2.24\pm0.09 $ 

$ 1.51\pm0.23 $ 

2.28646 $ \Xi_c $ 

$ 2.45\pm0.10 $ 

$ 2.21\pm0.35 $ 

2.46795 $ \Lambda_b $ 

$ 5.61\pm0.12 $ 

$ 1.96\pm0.36 $ 

5.6196 $ \Xi_b $ 

$ 5.79\pm0.09 $ 

$ 2.23\pm0.35 $ 

5.7919 $ \Lambda_c({{2S}}) $ 

$ 2.78\pm0.08 $ 

$ 3.20\pm0.48 $ 

2.7666 $ \Xi_c({{2S}}) $ 

$ 2.96\pm0.09 $ 

$ 4.48\pm0.56 $ 

2.9671 $ \Lambda_b({{2S}}) $ 

$ 6.08\pm0.09 $ 

$ 6.35\pm0.93 $ 

6.0723 $\Xi_b({{2S} })$ 

$ 6.24\pm0.07 $ 

$ 8.36\pm1.05 $ 

$ \Lambda_c({{3S}}) $ 

3.1749 $\Xi_c({{3S} })$ 

3.3936 $ \Lambda_b({{3S}}) $ 

6.4935 Table 2. Masses and pole residues of the heavy baryon states, where the masses of
$\Lambda_c({{3S}})$ ,$ \Xi_c({{3S}}) $ , and$ \Lambda_b({{3S}}) $ are obtained from the Regge trajectories.In this article, we have neglected the perturbative
$ {\cal O}(\alpha_s) $ corrections; if we consider the perturbative$ {\cal O}(\alpha_s) $ corrections, the perturbative terms should be multiplied by a factor$1+C(s,m_Q^2)\dfrac{\alpha_s(T^2)}{\pi}$ , where$ C(s, m_Q^2) $ are coefficients. Although we cannot estimate the uncertainties originating from the$ {\cal O}(\alpha_s) $ corrections with confidence without explicit calculations, a crude estimation is still possible. In the case of the proton and neutron, we can set$ m_u = m_d = 0 $ , and obtain the coefficient$C = {53}/{12}+ \gamma_E$ [53]. If we take the approximation$C(s,m_Q^2) = {53}/{12}+\gamma_E$ , we can obtain the central values$ M_{\Lambda_{c/b}} = 2.29/5.64\,{\rm{GeV}} $ instead of$ 2.24/5.61\,{\rm{GeV}} $ ; compared to the experimental values$ 2.29/5.62\,{\rm{GeV}} $ from the Particle Data Group [51], the central values$ M_{\Lambda_{c/b}} = 2.29/5.64\,{\rm{GeV}} $ are excellent. In fact, we should also calculate the perturbative$ {\cal O}(\alpha_s) $ corrections to the four-quark condensates$ \langle\bar{q}q\rangle^2 $ , as they play an important role, and re-determine the Borel windows to extract the heavy baryon masses, as in the case of the heavy mesons, in which the perturbative$ {\cal O}(\alpha_s) $ corrections to the quark condensates$ \langle\bar{q}q\rangle $ are also calculated [54]. Overall, neglecting the perturbative$ {\cal O}(\alpha_s) $ corrections cannot notably impair the predictive ability, because as we obtain the heavy baryon masses from fractions, the perturbative$ {\cal O}(\alpha_s) $ corrections in the numerators and denominators cancel each other out to a certain extent; see Eq. (15).In Fig. 3, we plot the predicted mass of the ground state
$ \Lambda_c $ with variations of the Borel parameter$ T^2 $ by considering the vacuum condensates up to dimension 6, 8, and 10, respectively, for the continuum threshold parameter$ \sqrt{s_0} = 2.75\,{\rm{GeV}} $ . From the figure, we can see that the truncation$ D = 6 $ fails to lead to a flat platform or to reproduce the experimental value of the mass of$ \Lambda_c $ , whereas the truncations$ D = 8 $ and$ 10 $ both lead to very flat platforms and reproduce the experimental value. In fact, the truncations$ D = 8 $ and$ 10 $ make little difference, which indicates that the vacuum condensates of dimension 8 (10) play an important (a minimal) role. We should consider the vacuum condensates up to dimension 10 for consistency. If we insist on taking the truncation$ D = 6 $ , we have to choose a much larger continuum threshold parameter$ \sqrt{s_0} = 3.0\,{\rm{GeV}} $ , and the predicted mass increases monotonically with the increase of the Borel parameter$ T^2 $ ; we can reproduce the experimental value of the mass of$ \Lambda_c $ with a suitable Borel parameter but large uncertainty.
Figure 3. (color online) Mass of
$ \Lambda_c $ with variations of the Borel parameter$ T^2 $ , where$ D = 6 $ , 8, and 10 denote truncations of the vacuum condensates up to dimension 6, 8, and 10, respectively. The star$ * $ denotes the continuum threshold parameter$ \sqrt{s_0} = 3.0\,{\rm{GeV}} $ , and "Expt" denotes the experimental value.In QCDSR II, we can borrow some ideas from the conventional charmonium states. The masses of the ground state, first radial excited state, and second excited state of the charmonium states are
$m_{J/\psi} = 3.0969\, {\rm{GeV}}$ ,$ m_{\psi^\prime} = 3.686097\,{\rm{GeV}} $ , and$ m_{\psi^{\prime\prime}} = 4.039\,{\rm{GeV}} $ , respectively, from the Particle Data Group [51]. The energy gaps are$ m_{\psi^\prime}-m_{J/\psi} = 0.59\,{\rm{GeV}} $ and$ m_{\psi^{\prime\prime}}-m_{J/\psi} = 0.94\,{\rm{GeV}} $ , and we can choose the continuum threshold parameters$\sqrt{s_0^\prime}\leqslant M_{gr}+ 0.90\,{\rm{GeV}}$ tentatively to avoid contaminations from the second radial excited states. Furthermore, we choose the energy scales of the QCD spectral densities in the QCD sum rules for$\Lambda_c({{2S}})$ ,$\Xi_c({{2S}})$ ,$\Lambda_b({{2S}})$ , and$\Xi_b({{2S}})$ to be the typical energy scales$ \mu = 2\,{\rm{GeV}} $ ,$ 2\,{\rm{GeV}} $ ,$ 4\,{\rm{GeV}} $ , and$ 3.8\,{\rm{GeV}} $ , respectively; again we subtract$ 0.2\,{\rm{GeV}} $ from the energy scale for$\Xi_b({{2S}})$ to account for the finite mass of the s-quark. After trial and error, we obtain the Borel parameters$ T^2 $ , continuum threshold parameters$ s_0 $ , pole contributions, and perturbative contributions, which are shown explicitly in Table 1. From the table, we can see that the pole contributions vary from 40% to 80%, so the pole dominance is satisfied. The perturbative contributions are larger than 70%, so the operator product expansion is well convergent.Again we consider all uncertainties of the input parameters, and obtain the values of the masses and pole residues of the first radial excited states of the flavor antitriplet heavy baryon states, which are also shown in Figs. 1-2 and Table 2. From Table 1 and Figs. 1-2, we can see that rather flat platforms appear in the Borel windows, and the uncertainties originating from the Borel parameters are rather small. The predicted masses
$M_{\Lambda_b({\rm{2S}})} = 6.08\pm0.09\,{\rm{GeV}}$ ,$ M_{\Lambda_c({\rm{2S}})} = 2.78\pm0.08\,{\rm{GeV}} $ , and$M_{\Xi_c({\rm{2S}})} = 2.96\pm0.09\,{\rm{GeV}}$ are in excellent agreement with the experimental data$ 6072.3\pm 2.9\pm 0.6\pm 0.2\,{\rm{MeV}} $ ,$2766 .6\pm2.4\, {\rm{MeV}}$ , and$ 2967 .1 \pm1.4\,{\rm{MeV}} $ , respectively [2, 51], and support assigning$ \Lambda_b(6072) $ ,$ \Lambda_c(2765) $ and$ \Xi_c(2980/2970) $ to be the first radial excited states of$ \Lambda_b $ ,$ \Lambda_c $ and$ \Xi_c $ , respectively. The prediction$ M_{\Xi_b({\rm{2S}})} = 6.24\pm0.07\,{\rm{GeV}} $ can be confronted by experimental data in the future.If the masses of the ground states, first radial excited states, third radial excited states, etc. of the heavy baryon states
$ \Lambda_Q $ and$ \Xi_Q $ satisfy the Regge trajectories,$ M_n^2 =\alpha (n-1)+\alpha_0\, , $

(25) with two parameters
$ \alpha $ and$ \alpha_0 $ , we take the experimental values of the masses of the ground states and first radial excited states shown in Table 2 as input parameters to fit$ \alpha $ and$ \alpha_0 $ , and obtain the masses of the second radial excited states, which are also shown in Table 2 as the "experimental values". From Tables 1-2, we can see that the continuum threshold parameters$\sqrt{s_0^\prime}\leqslant M_{\Lambda_c({{3S}})}$ ,$M_{\Xi_c({{3S}})}$ and$M_{\Lambda_b({{3S}})}$ , respectively; the contaminations from the second radial excited states are excluded. The central values have the relations$\sqrt{s^{\prime}_0}-M_{{{2S}}} = (0.20-0.30)\,{\rm{GeV}}$ and$M_{{{3S}}}-\sqrt{s^{\prime}_0} = (0.15- 0.20)\,{\rm{GeV}}$ , and the continuum threshold parameters$ s^\prime_0 $ are large enough to consider all the first radial excited state contributions but small enough to exclude the second radial excited state contaminations. The central values$\sqrt{s^{\prime}_0}-M_{gr} = (0.70- 0.80)\,{\rm{GeV}}$ , which are consistent with the experimental value$ m_{\psi^{\prime\prime}}-m_{J/\psi} = 0.94\,{\rm{GeV}} $ [51].In Ref. [5], Liang and Lu study the strong decay behaviors under various assignments of
$ \Lambda_b(6072) $ within the$ {}^3P_0 $ model, and obtain the conclusion that$ \Lambda_b(6072) $ can be assigned to be the$ \rho $ -mode excitation of the$ \Lambda_b $ family with the spin-parity$J^P = {{1}/{2}}^-$ by introducing mixing effects between the$ s_l = 0 $ and$ s_l = 1 $ states, where$ s_l $ denotes the angular momentum of the light degrees of freedom. Accordingly, we can introduce the relative P-wave between the u and d quarks explicitly and construct the current$ J(x) $ to interpolate$ \Lambda_b(6072) $ :$ \begin{aligned}[b]J(x)& = J_0(x) \cos\theta+J_1(x) \sin\theta\, , \\ J_0(x)& =\varepsilon^{ijk} u^T_i(x)C\gamma^\alpha \stackrel{\leftrightarrow}{\partial}_\alpha d_j(x) b_k(x)\, ,\\ J_1(x)& =\varepsilon^{ijk} u^T_i(x)C\gamma_\alpha \stackrel{\leftrightarrow}{\partial}_\beta d_j(x) \sigma^{\alpha\beta} b_k(x)\, , \end{aligned} $

(26) where
$ \stackrel{\leftrightarrow}{\partial}_\alpha = \overrightarrow{\partial}_\alpha-\overleftarrow{\partial}_\alpha $ . Without directly calculating the mass and decay width, we cannot obtain the conclusion as to whether or not the QCD sum rules support such an assignment; this is the subject of our next work.The spin-parities of the ground states
$ \Lambda_c $ ,$ \Xi_c $ ,$ \Lambda_b $ , and$ \Xi_b $ have been established; the values listed in the Review of Particle Physics are$J^P = {{1}/{2}}^+$ [51]. In this article, we study the masses and pole residues of the ground states and first radial excited states of the flavor antitriplet heavy baryons, and make possible assignments of$ \Lambda_b(6072) $ ,$ \Lambda_c(2765) $ and$ \Xi_c(2980/2970) $ according to the predicted masses, as their spin-parities have not been established yet. The present predictions support assigning$ \Lambda_b(6072) $ ,$ \Lambda_c(2765) $ , and$ \Xi_c(2980/2970) $ to be the first radial excitations of$ \Lambda_b $ ,$ \Lambda_c $ , and$ \Xi_c $ , respectively, although more theoretical and experimental works are required to make more reliable assignments. There is no experimental candidate for the$ \Xi_c({\rm{2S}}) $ state. After the manuscript was submitted to https://arxiv.org, and appeared as arXiv: 1704.01854, the Belle collaboration determined the spin-parity of$ \Xi_c(2970)^+ $ to be${{1}/{2}}^+$ for the first time [55], which is consistent with the present calculation. -
In this article, we construct
$ \Lambda $ -type currents to study the ground states and first radial excited states of the flavor antitriplet heavy baryon states$ \Lambda_Q $ and$ \Xi_Q $ with spin-parity$ J^P = {1\over 2}^{+} $ by subtracting the contributions from the corresponding heavy baryon states with spin-parity$ J^P = {1\over 2}^{-} $ via the QCD sum rules. We carry out the operator product expansion up to the vacuum condensates of dimension$ 10 $ in a consistent way, observe that the higher dimensional vacuum condensates play an important role, and obtain very stable QCD sum rules with variations of the Borel parameters for the ground states for the first time. We then study the masses and pole residues of the first radial excited states in detail; the predicted masses$M_{\Lambda_b({{2S}})} = 6.08\pm0.09\,{\rm{GeV}}$ ,$M_{\Lambda_c({{2S}})} = 2.78\pm0.08\,{\rm{GeV}}$ and$M_{\Xi_c({{2S}})} = 2.96\pm0.09\,{\rm{GeV}}$ are in excellent agreement with the experimental data, and support assigning$ \Lambda_b(6072) $ ,$ \Lambda_c(2765) $ , and$ \Xi_c(2980/2970) $ to be the first radial excited states of$ \Lambda_b $ ,$ \Lambda_c $ , and$ \Xi_c $ , respectively. Finally, we use the Regge trajectories to obtain the masses of the second radial excited states and observe that the continuum threshold parameters are reasonable to avoid contaminations from the second radial excited states.
Analysis of the 1S and 2S states of ΛQ and ΞQ with QCD sum rules
- Received Date: 2020-07-02
- Available Online: 2021-01-15
Abstract: In this article, we study the ground states and the first radial excited states of the flavor antitriplet heavy baryon states






 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF































 DownLoad:
DownLoad: