-
Hadron spectroscopy is a tool to reveal the dynamics of the quark interactions within composite systems like baryons, mesons, and exotics. The phenomenological approach of hadron spectroscopy uses potentials to establish the resonance masses of higher radial and orbital states of hadrons. The various possible decays of a resonance state also help in identifying short-lived hadrons and even missing excited states. A number of resonance states of light and heavy hadrons have been provided by the Particle Data Group [1].
The specific target here is the study of the
$ \Delta $ baryon, a member of the baryon decuplet ($J^{P} = {3}/{2}^{+}$ ) which is composed of light u and d quarks. Despite having the same nucleon composition, the four possible combinations of the symmetric wave function gives four$ \Delta $ particles with isospin$I = {3}/{2}$ :$ \Delta^{++} $ (uuu,$I_{3} = {3}/{2}$ ),$ \Delta^{+} $ (uud,$I_{3} = {1}/{2}$ ),$ \Delta^{0} $ (udd,$I_{3} = - {1}/{2}$ ) and$ \Delta^{-} $ (ddd,$I_{3} = - {3}/{2}$ ). The present work is motivated by the fact that heavy quark systems decay into light quark systems through various decay channels, and most matter is composed of these light quark systems.$ \Delta $ (1232) has been observed experimentally in pion-nucleon decays for quite a long time [2, 3], recent studies at HADES-GSI have continued to explore new properties [4].$ \Delta $ s, likely an excited state of a nucleon (N) with ground state 939 MeV, have been extensively studied through photoproduction decays at ELSA [5]. However, the symmetric flavour wavefunction of$ \Delta $ differs from the mixed symmetry wavefunction of nucleons. Thus, revealing every known and unknown property of$ \Delta $ baryons has always been a matter of interest, as discussed in many review articles [6-9]. The$ \Delta $ resonances shall also be the focus of upcoming experimental facilities at PANDA-GSI [10, 11].Phenomenological and theoretical models for light baryon studies have been developed and modified over time. The light baryon resonances have been explored through the well-known Isgur-Karl model basically applied for P-wave states [12] as well as modified with a relativised approach [13], the Goldstone-boson exchange model due to spontaneous chiral symmetry breaking [14, 15], a quark-diquark system with Gursey-Radicati exchange interaction [16, 17], and a semi-relativistic model with SU(6)-invariant and SU(6)-violating terms [18]. Lately, various approaches have been used, including QCD sum rules [19], the basic light-front model [20] and relativistic light-front model [21], lattice QCD [22], the covariant Faddeev approach [23], and others based on n and
$ J^{P} $ values and the respective trajectories against square of mass of a given state [24, 25]. The spectrum of octet and decuplet light baryons has also been studied in a relativistic approach using instanton induced quark forces [26].In this paper, a non-relativistic hypercentral contituent quark model (hCQM) has been employed to obtain the resonance masses of radial and orbital states of the
$ \Delta $ baryon [27-29]. The potential term consists of two parts: a Coulomb-like term and a confinement term. A similar method has been employed for heavy baryons using different potentials, including a screened potential [30], linear potential [31, 32], and so on.The paper is organized as follows. After this introduction, the theoretical framework is discussed. The third section incorporates the results and discussion of the mass spectra. Sections four, five and six deal with the baryon magnetic moment, Regge trajectory and decay widths respectively. Finally, conclusions are drawn in the last section.
-
Hadron spectroscopy is useful for better understanding of hadrons as bound states of quarks and gluons, as well as the spectrum and internal structure of excited baryons. This is a key to strong interactions in the region of quark confinement. The system becomes complex and difficult to deal with when all the quark-quark, quark-gluon and gluon-gluon interactions are considered. This is the reason for using the constituent quark mass, incorporating all the other effects in the form of some parameters.
A constituent quark model is a modelization of a baryon as a system of three quarks or anti-quarks bound by some kind of confining interaction. An effective way to study three body systems is through consideration of Jacobi coordinates as
$\tag{1a} { \rho} = \frac{1}{\sqrt{2}}({ r_{1}} -{ r_{2}}), $

$\tag{1b}{ {\lambda}} = \frac{{({{m}_{1}}{{{r}}_{{1}}} + {{m}_{2}}{{{r}}_{{2}}} - ({{m}_{1}} + {{m}_{2}}){{{r}}_{{3}}})}}{{\sqrt {{m}_{1}^{2} + {m}_{2}^{2} + {{({{m}_{1}} + {{m}_{2}})}^{2}}} }} ,$

$ x = \sqrt{\rho^{2}+ {\lambda^{2}}} ; \; \; \xi = \arctan\left(\frac{\rho}{\lambda}\right) , $

(2) where x is the hyperradius and
$ \xi $ is the hyperangle.The Hamiltonian of the system is expressed as
$ H = \frac{P^{2}}{2m} + V^{0}(x) + \frac{1}{m_{x}}V^{1}(x) + V_{SD}(x) , $

(3) where
$m = \dfrac{2m_{\rho}m_{\lambda}}{m_{\rho}+m_{\lambda}}$ is the reduced mass.The dynamics are considered in the wave-function
$ \psi(x) $ , which is the solution of the hyperradial equation$ \left[\frac{{\rm d}^{2}}{{\rm d}x^{2}} + \frac{5}{x}\frac{{\rm d}}{{\rm d}x} - \frac{\gamma(\gamma +4)}{x^{2}}\right]\psi(x) = -2m[E-V(x)]\psi(x) . $

(4) The potential incorporated solely depends on the hyperradius x of the system and not on the hyperangle [33].
$ V^{0}(x) = -\frac{\tau}{x} + \alpha x^{\nu}, $

(5) V(x) consists of a Coulomb-like term and a confining term, which is taken to be linear with power index
$ \nu $ = 1. Another part of the potential form is the first order correction term with$\dfrac{1}{m_{x}} = \left(\dfrac{1}{m_{\rho}} - \dfrac{1}{m_{\lambda}}\right)$ .$ V^{1}(x) = -C_{F}C_{A}\frac{\alpha_{s}^{2}}{4x^{2}}, $

(6) where
$ C_{F} $ and$ C_{A} $ are the Casimir elements of fundamental and adjoint representation.$ \alpha_{s} $ is the running coupling constant.Along with the zeroth and first order correction terms in the hypercentral approximation, a spin-dependent term
$ V_{SD} $ (x) is also incorporated to sharply distinguish the degenerate states [34].$\begin{aligned}[b] {V_{SD}}(x) =&{ {V_{SS}}(x)({{\bf{S}}_\rho } \cdot {{{S}}_\lambda }) + {V_{\gamma S}}(x)(\gamma \cdot {{S}})}\\ &{ + {V_T} \times \left[{S^2} - \frac{{3({{S}} \cdot {{x}})({{S}} \cdot {{x}})}}{{{x^2}}}\right]}, \end{aligned}$

(7) where
$ V_{SS}(x) $ ,$ V_{\gamma S}(x) $ and$ V_{T}(x) $ are spin-spin, spin-orbit and tensor terms respectively.The quark masses are taken as
$ m_{u} = m_{d} = 0.290 $ GeV. The numerical solution of the six-dimensional Schrodinger equation was performed using Mathematica Notebook [35]. -
Based on the model and potential terms discussed in the above section, the resonance masses from 1S-5S, 1P-5P, 1D-4D and 1F-2F with allowed spin-parity assignments have been computed as shown in Table 1. In addition, the present results are compared with previous results calculated using different models, for available states.
State $ J^{P} $ 

Present model PDG[1] Status [15] [16] [17] [18] [27] [25] [12] [13] [24] 1S $ \dfrac{3}{2}^{+} $ 

1232 1230-1234 **** 1232 1235 1247 1231 1232 1232 1232 1230 1232 2S $ \dfrac{3}{2}^{+} $ 

1611 1500-1640 **** 1659.1 1714 1689 1658 1727 1625 1600 3S $ \dfrac{3}{2}^{+} $ 

1934 1870-1970 *** 2090.2 1914 1921 1920 4S $ \dfrac{3}{2}^{+} $ 

2256 − − 5S $ \dfrac{3}{2}^{+} $ 

2579 − − 1P $ \dfrac{1}{2}^{-} $ 

1609 1590-1630 **** 1667.2 1673 1830 1737 1573 1645 1685 1555 1P $ \dfrac{3}{2}^{-} $ 

1593 1690-1730 **** 1667.2 1673 1830 1737 1573 1720 1685 1620 1P $ \dfrac{5}{2}^{-} $ 

1550 − − 2P $ \dfrac{1}{2}^{-} $ 

1956 1840-1920 *** 2003 1910 1910 1900 2P $ \dfrac{3}{2}^{-} $ 

1919 1940-2060 ** 1910 1940 2P $ \dfrac{5}{2}^{-} $ 

1871 1900-2000 *** 2003 1910 1908 1945 3P $ \dfrac{1}{2}^{-} $ 

2280 − * 2150 3P $ \dfrac{3}{2}^{-} $ 

2242 − − 3P $ \dfrac{5}{2}^{-} $ 

2193 − − 4P $ \dfrac{1}{2}^{-} $ 

2602 − − 4P $ \dfrac{3}{2}^{-} $ 

2565 − − 4P $ \dfrac{5}{2}^{-} $ 

2515 − − 5P $ \dfrac{1}{2}^{-} $ 

2926 − − 5P $ \dfrac{3}{2}^{-} $ 

2888 − − 5P $ \dfrac{5}{2}^{-} $ 

2836 − − 1D $ \dfrac{1}{2}^{+} $ 

1905 1850-1950 **** 1873.5 1930 1827 1891 1953 1895 1910 1D $ \dfrac{3}{2}^{+} $ 

1868 1870-1970 *** 1930 2042 1935 1920 1D $ \dfrac{5}{2}^{+} $ 

1818 1855-1910 **** 1873.5 1930 2042 1891 1901 1895 1905 1D $ \dfrac{7}{2}^{+} $ 

1756 1915-1950 **** 1873.5 1930 2042 1891 1955 1950 1950 2D $ \dfrac{1}{2}^{+} $ 

2227 − − 2D $ \dfrac{3}{2}^{+} $ 

2190 − − 2D $ \dfrac{5}{2}^{+} $ 

2140 − ** 2200 2D $ \dfrac{7}{2}^{+} $ 

2078 − − 3D $ \dfrac{1}{2}^{+} $ 

2556 − − 3D $ \dfrac{3}{2}^{+} $ 

2516 − − Continued on next page Table 1. Resonance masses of
$ \Delta $ baryons (in MeV).Table 1-continued from previous page State $ J^{P} $ 

Present model PDG[1] Status [15] [16] [17] [18] [27] [25] [12] [13] [24] 3D $ \dfrac{5}{2}^{+} $ 

2463 − − 3D $ \dfrac{7}{2}^{+} $ 

2397 − − 4D $ \dfrac{1}{2}^{+} $ 

2874 − − 4D $ \dfrac{3}{2}^{+} $ 

2835 − − 4D $ \dfrac{5}{2}^{+} $ 

2784 − − 4D $ \dfrac{7}{2}^{+} $ 

2720 − − 1F $ \dfrac{3}{2}^{-} $ 

2165 − − 1F $ \dfrac{5}{2}^{-} $ 

2108 − − 1F $ \dfrac{7}{2}^{-} $ 

2037 2150-2250 *** 2200 1F $ \dfrac{9}{2}^{-} $ 

1952 − − 2F $ \dfrac{3}{2}^{-} $ 

2486 − − 2F $ \dfrac{5}{2}^{-} $ 

2430 − * 2350 2F $ \dfrac{7}{2}^{-} $ 

2359 − − 2F $ \dfrac{9}{2}^{-} $ 

2274 − ** 2400 The four-star status assigned by the Particle Data Group (PDG) indicates the certainty of its existence with known properties. The radial states comprise of
$J^{P} = {3}/{2}^{+}$ , the 2S(1600) mass predicted as 1611 MeV differs by 11 MeV from Ref. [24], 14 MeV from Ref. [25] and nearly 47 MeV from Refs. [15, 18]. Similarly the 3S(1920) mass of 1934 MeV falls within the PDG range and differs only by 1-14 MeV from some references.The first orbital excited state 1P(1620) with
${1}/{2}^{-}$ is well within the range of PDG and differs by 36 MeV from Ref. [25]. However, the 1P(1700) state predicted with mass 1593 MeV (${3}/{2}^{-}$ ) is under-predicted by 97 MeV from the lower range of experimental data. The three-star states of 2P with spin-parity assignment${1}/{2}^{-}$ and${5}/{2}^{-}$ are over- and under-predicted respectively compared to the PDG ranges.The four-star designated second orbital state 1D with
${1}/{2}^{+}$ is obtained as 1905 MeV differs by 5 MeV from Ref. [24] and by 25 MeV from Ref. [16]. The two states with (${5}/{2}^{+}, {7}/{2}^{+}$ ) have been predicted to be quite low compared to known data as well as other references. Based on the current results, the$ \Delta(1920) $ state from the PDG might be assigned to 1D(${3}/{2}^{+}$ ) or 3S(${3}/{2}^{+}$ ) based on the comparison shown in the table.The predicted 1F
${7}/{2}^{-}$ mass of 2037 MeV is 113 MeV less than the lower limit of the PDG range. However, the present study has attempted to predict many unknown states too, which are the least explored by other models and experiments. -
The baryon magnetic moment plays a crucial role in providing information regarding the structures and shapes of baryons [36]. The magnetic moment of
$ \Delta^{++} $ has been precisely measured through pion bremsstrahlung analysis [37]. Theoretically, the magnetic moments of$J^{P} = {3}/{2}^{+}$ decuplet baryons have been calculated through different approaches, including the quark model with QCD sum rules [38], chiral quark model [39, 40], and the color dielectric model [41]. However, none of the calculations account for complicated effects due to valence quarks, pion clouds, exchange currents, constituent quark mass, etc, and are thus neglected. In the present study, the effective quark mass has been considered to obtain the magnetic moments of all four$ \Delta $ isospin states. The baryon magnetic moment is expressed as [42]$ \mu_{B} = \sum_{q} \left\langle \phi_{sf} \vert \mu_{qz}\vert \phi_{sf} \right\rangle, $

(8) where
$ \phi_{sf} $ is the spin-flavour wave function.$ \mu_{qz} = \frac{e_{q}}{2m_{q}^{\rm eff}}\sigma_{qz} . $

(9) The effective quark mass
$m_{q}^{\rm eff}$ is different from the model-based mass, as within the baryon, the mass may vary due to interactions among quarks.$ m_{q}^{\rm eff} = m_{q}\left(1+\frac{\langle H \rangle}{\sum_{q}m_{q}}\right), $

(10) where
$\langle H \rangle = E + \langle V_{\rm spin} \rangle$ [42]. A similar study for$ N^{*} $ has been done by Zalak Shah et al. [33].The result in Table 2 shows that the
$ \Delta $ magnetic moments obtained from the present work are in accordance with experimental results. Reference [39] has compared magnetic moments using different sets of data; so based on that non-relativistic quark model, the$ \Delta^{++} $ magnetic moment is 5.43$ \mu_{N} $ , differing by 0.86$ \mu_{N} $ . The magnetic moments for$ \Delta^{+} $ and$ \Delta^{-} $ are 2.72$ \mu_{N} $ and -2.72$ \mu_{N} $ respectively, which differs by 0.48$ \mu_{N} $ .State Wave-function $\mu$ 

exp(PDG) [37] $\Delta^{++}$ 

3 $\mu_{u}$ 

4.568 $\mu_{N}$ 

4.52 $\mu_{N}$ 

$\Delta^{+}$ 

2 $\mu_{u}+\mu_{d}$ 

2.28 $\mu_{N}$ 

2.7 $\mu_{N}$ 

$\Delta^{0}$ 

2 $\mu_{d}+\mu_{u}$ 

0 − $\Delta^{-}$ 

3 $\mu_{d}$ 

−2.28 $\mu_{N}$ 

− Table 2. Magnetic moments of Δ(1232) isospin states.
-
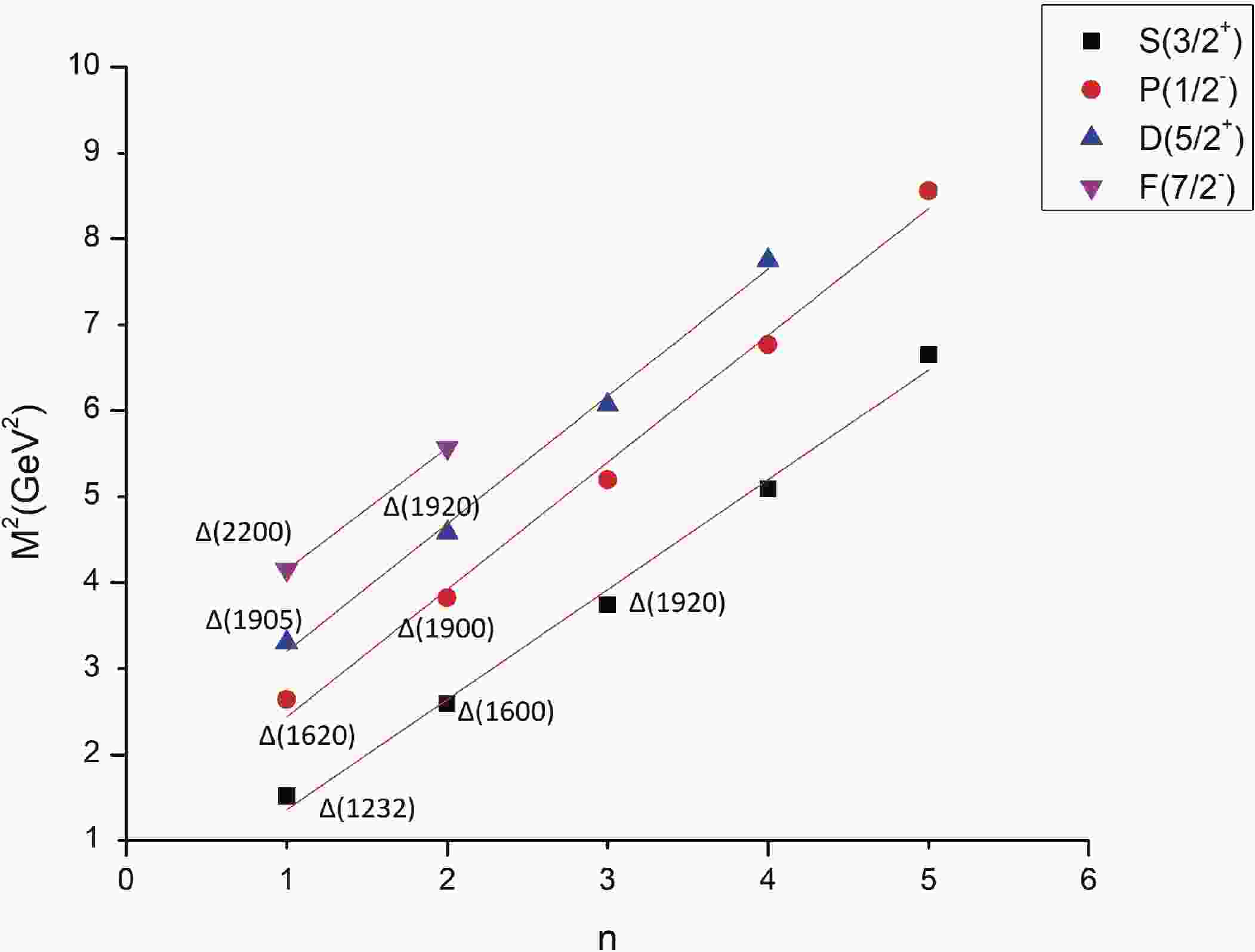
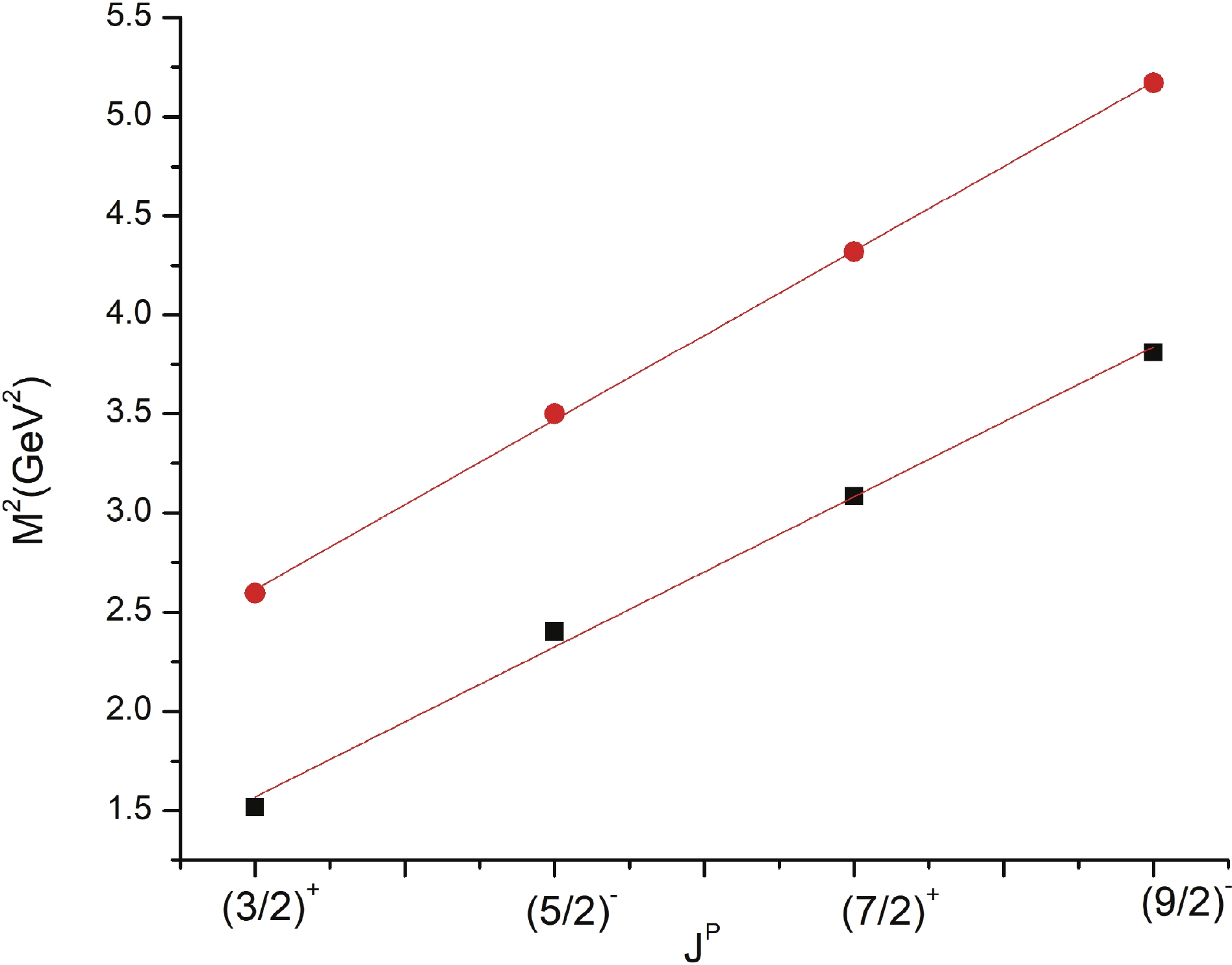
An important property concluded from the baryon spectrum is the plot of J, total angular momentum against
$ M^{2} $ , as well as the principal quantum number n against$ M^{2} $ . These lines are so far observed to be linear and non-intersecting for the light baryon spectrum [43]. These plots provide a confirmation between the experimental and theoretical predicted masses of excited states with their respective quantum numbers [44]. This holds true for positive and negative parity states as well. Regge trajectories have been widely employed in heavy hadron studies too [45, 46]. The equations are as follows$ \tag{11a} J = \alpha M^{2} + \alpha_{0}, $

$\tag{11b} n = \beta M^{2} + \beta_{1} . $

The trajectory in Fig. 1, based on Eq. (11b), shows that the calculated data are in good agreement with the nature of the experimental data, as all the calculated resonance squared masses fall on the linear curve. Also, a few individual experimental points marked in the graph agree with the total angular momentum and spin configuration assigned in the calculated data.
The plot of total angular momentum quantum number J with natural parity P against the squared mass is shown in Fig. 2 , and also follows a linear curve.
-
The observations of decays of baryon resonances afford valuable guidance in assigning the resonances their correct places in various symmetry schemes. The correct isotopic spin assignment is likely to be implied by the experimental branching ratio into different charge states of particles produced by the decay, while experimental decay widths provide a means of extracting phenomenological coupling constants.
The chiral quark model, in which constituent quarks couple directly to mesons, is known to describe the properties of the ground state octet and decuplet baryons quite well [47].
The prominent decay channel for nucleons, including
$ \Delta $ , has been observed to be$ N^{*} $ and pion, depending on the charge of the respective parent [48]. The transition couplings of vector mesons have been obtained along with other constants by Riska et al. [49]. In the present work, the constants and decay widths provided by Particle Data Group have been employed to establish the decay widths of some well-established resonance masses. For the$ \Delta(1600) $ decay to$ N\pi $ ,$ \Gamma = \frac{1}{3}\frac{f^{2}}{4\pi}\frac{E^{'}+m_N}{m^{*}}\frac{k^{3}}{m_{\pi}^{2}}, $

(12) where
$ E^{'} $ is the energy of the final nucleon and k is the pion momentum.$ E^{'} = \frac{m^{*2}-m_{\pi}^{2}+m_N^{2}}{2m^{*}}, $

(13) $ k = \frac{\sqrt{[m^{*2}-(m_N + m_{\pi})^{2}][m^{*2}-(m_N - m_{\pi})^{2}]}}{2m^{*}}. $

(14) Here
$ m^{*} $ is the resonance mass calculated using the above model,$ m_{N} $ is the nucleon mass 939 MeV and$ m_{\pi} $ is the pion mass 139 MeV. Using$ m^{*} = 1611 $ and$ f = 0.51 $ , Γ = 24.8% , which is well within the PDG range of 8%-24%.For
$ \Delta(1620) $ decaying to$ N\pi $ ,$ \Gamma = \frac{f^{2}}{4\pi}\frac{E^{'}+m_N}{m^{*}}\frac{k}{m_{\pi}^{2}}(m^{*}-m_{N})^{2}, $

(15) $ m^{*} = 1609 $ ,$ f = 0.34 $ , and Γ = 92% , whereas the PDG range is 25%-35%.For
$ \Delta(1700) $ decaying to$ N\pi $ ,$ \Gamma = \frac{1}{3}\frac{f^{2}}{4\pi}\frac{E^{'}-m_N}{m^{*}}\frac{k^{3}}{m_{\pi}^{2}}, $

(16) $ m^{*} = 1593 $ ,$ f = 1.31 $ , and Γ = 14.83% , whereas the PDG range is 10%-20%. -
In the present work,
$ \Delta $ resonance masses have been calculated using the hypercentral constituent quark model employed with a linear potential. The first order corrections have also been included. All the masses up to the 2F states have been compared with available experimental data as well as different theoretical and phenomenological models in Table 1. Therein$ \Delta(1232) $ ,$ \Delta(1600) $ ,$ \Delta(1620) $ ,$ \Delta(1700) $ ,$ \Delta(1905) $ ,$ \Delta(1910) $ and$ \Delta(1950) $ as well as the three-star states$ \Delta(1900) $ ,$ \Delta(1920) $ $ \Delta(1930) $ and$ \Delta(2200) $ , and other fairly established states, have been predicted.It is evident that the radial excited states as well as orbital excited states with lower spin state agree to a considerable level with the PDG range and a few of the models discussed in Section III. However, the higher spin states of orbital excited states are mostly under-predicted compared to the experimental range.
The Regge trajectories have been plotted with principal quantum number n and angular momentum J against the square of the resonance mass. Figure 1 shows that the Regge trajectories are linear but not exactly parallel. However, the experimental points are not very far from the respective lines. Figure 2 resolves that the spin-parity assignment for orbital excited states also follows a linear relation.
The baryon magnetic moment has been calculated for all four isospin states of
$ \Delta $ as described in Table 2. However, the values of two isospin states have not been obtained experimentally so far. The$ \Delta^{++} $ magnetic moment is close to the PDG value and the$ \Delta^{+} $ magnetic moment differs by 0.58$ \mu_{N} $ from that of the PDG.Finally, decay widths have been obtained for strong decays through the
$ N\pi $ channel for the three states$ \Delta(1600) $ ,$ \Delta(1620) $ and$ \Delta(1700) $ , using the nucleon to vector meson transition couplings. For$ \Delta(1600) $ and$ \Delta(1700) $ the decay widths are well within the range but the$ \Delta(1620) $ decay width predicted is higher than the experimental range.Thus, the present work has effectively explored the known and unknown properties of the
$ \Delta $ baryon in a similar approach to that of earlier N* spectroscopy [33]. The accomplishments and shortcomings from this study are expected to inspire improvements and further exploration of other light baryons, including at experimental facilities such as PANDA-GSI [10, 11]. -
One of the authors, Ms. Chandni Menapara, would like to acknowledge support from the Department of Science and Technology (DST) under the INSPIRE-FELLOWSHIP scheme.
Spectroscopic properties of Δ baryons
- Received Date: 2020-09-05
- Available Online: 2021-02-15
Abstract: The resonance state of the





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF



















 DownLoad:
DownLoad: