-
The investigation of nuclear systems involving weakly-bound (WB) nuclei at energies near the Coulomb barrier (VB) is a subject of sustained interest in nuclear physics [1, 2]. Among these WB nuclei, 7Li is particularly noteworthy owing to its pronounced α + t structure and relatively low binding energy of approximately 2.468 MeV. Such a unique structure can significantly influence reaction mechanisms. Furthermore, investigations of nuclear reactions involving WB stable ions have revealed numerous unconventional behaviors [3].
This work focuses on understanding the scattering mechanism of 7Li projectiles from 118,120Sn isotopes at energies near and above the VB. We examine the 7Li + 118Sn nuclear system at energies (Elab) ranging from 18.15 to 48 MeV [4−6], and 7Li + 120Sn at Elab between 20 and 44 MeV [7−9]. These systems have been the subject of extensive experimental measurements [4−12] and theoretical investigations [13−20]. Previous studies have provided valuable insights into these systems. For instance, Ref. [13] examined the scattering of 6,7Li from 120Sn and 26Mg nuclei at Elab = 44 MeV, evaluating both cross sections and analyzing powers through coupled-channel calculations. These calculations successfully reproduced the measured data when the interaction strength was significantly reduced to compensate for overestimation at the nuclear surface region. Similarly, Ref. [14] examined 7Li scattering by 120Sn at Elab = 44 MeV within a coupled-channel framework, considering virtual projectile excitations. Both cluster folding (CF) and double-folding (DF) interactions were employed, yielding excellent agreement with experimental data for cross sections, vector analyzing power (VAP), and higher-rank tensor observables in both elastic and inelastic scattering.
The derivation of 7Li+nucleus potentials has been approached through both phenomenological [16, 17] and microscopic [18, 19] methods. For instance, Cook [16] conducted simultaneous fits to multiple 6,7Li datasets spanning mass numbers 24−208 to establish a global optical potential (OP) for 6,7Li scattering. The analysis revealed that Woods-Saxon (WS) form factors with constant parameters could be used for all potential components except the imaginary potential depth, which decreased with increasing target mass. Notably, the real potential depth was found to be identical for projectiles, resulting in a smaller volume integral for 7Li. Additionally, the imaginary volume integral was smaller for 7Li than for 6Li, indicating weaker absorption for 7Li.
In a complementary study, Y. Xu et al. [17] proposed a global phenomenological optical model (OM) potential for 7Li projectiles, based on elastic scattering ADs and reaction cross-section (σR) data for target nuclei ranging from 27Al to 208Pb at energies below 200 MeV. This potential provided satisfactory descriptions of 7Li elastic scattering across the studied systems. Microscopic approaches have also contributed significantly to our understanding. Xu and Pang [18] introduced a global potential by analyzing ADs from 6,7Li elastic scattering off targets (A ≥ 40) at Elab = 5–40 MeV/u. The single-folding model, incorporating the JLMB nucleon-nucleus interaction [21, 22] provided good agreement with experimental σR and AD data. In a more fundamental approach, Chen et al. [19] developed a microscopic OP for 7Li+nucleus systems without adjustable parameters. This potential was constructed by folding the microscopic OP of the cinstitutent nucleons of 7Li over their density distributions, with the internal wave function described using the harmonic oscillator shell model. The resulting potential successfully predicted ADs and σR for targets ranging from A = 27 to 208 at energies below 450 MeV, demonstrating comparable performance to that of global phenomenological potentials. Basak et al. [20] provided additional insights through the analysis of elastic scattering cross sections and VAP for 6,7Li scattered from 12C, 26Mg, 58Ni, and 120Sn nuclei. Their OM calculations employed a real folded potential based on realistic two-nucleon interactions, requiring no normalization, along with imaginary and spin-orbit potentials. This approach successfully accounted for both cross section and VAPs, including the explanation of opposite signs observed in VAP data for 6,7Li + 58Ni and 6,7Li + 120Sn systems at Elab = 20 and 44 MeV, respectively.
This work presents a comprehensive investigation of elastic scattering cross sections for 7Li projectiles on 118,120Sn targets across a broad energy range. Utilizing multiple nuclear potential models and computational approaches, we systematically compare theoretical predictions with experimental data. A key focus of our analysis is the determination of the necessary normalization factors required to achieve optimal agreement with the AD data for both 7Li + 118Sn and 7Li + 120Sn systems. The rest of this paper is structured as follows: Sec. II details the theoretical framework and potential models employed in our calculations, Sec. III presents and analyzes the results, and Sec. IV summarizes our principal findings and conclusions.
-
The investigation of nuclear systems involving weakly bound (WB) nuclei at energies near the Coulomb barrier (VB) is a subject of sustained interest in nuclear physics [1, 2]. Among these WB nuclei, 7Li is particularly noteworthy due to its pronounced α + t structure and relatively low binding energy of approximately 2.468 MeV. This unique structure can significantly influence reaction mechanisms. Furthermore, investigations of nuclear reactions involving WB stable ions have revealed numerous unconventional behaviors [3].
This work focuses on understanding the scattering mechanism of 7Li projectiles from 118,120Sn isotopes at energies near and above the VB. We examine the nuclear systems 7Li + 118Sn at energies (Elab) ranging from 18.15 to 48 MeV [4-6], and 7Li + 120Sn at Elab between 20 and 44 MeV [7-9]. These systems have been the subject of extensive experimental measurements [4-12] and theoretical investigations [13-20]. Previous studies have provided valuable insights into these systems. For instance, Ref. [13] examined the scattering of 6,7Li from 120Sn and 26Mg nuclei at Elab = 44 MeV, analyzing both cross sections and analyzing powers through coupled-channel calculations. These calculations successfully reproduced the measured data when the interaction strength was significantly reduced to compensate for overestimation at the nuclear surface region. Similarly, Ref. [14] examined 7Li scattering by 120Sn at Elab = 44 MeV within a coupled-channel framework, considering virtual projectile excitations. Both cluster folding (CF) and double-folding (DF) interactions were employed, yielding excellent agreement with experimental data for cross sections, vector analyzing power (VAP), and higher-rank tensor observables in both elastic and inelastic scattering.
The derivation of 7Li+nucleus potentials has been approached through both phenomenological [16, 17] and microscopic [18, 19] methods. For instance, Cook [16] conducted simultaneous fits to multiple 6,7Li datasets spanning mass numbers 24-208 to establish a global optical potential (OP) for 6,7Li scattering. The analysis revealed that Woods-Saxon (WS) form factors with constant parameters could be used for all potential components, except the imaginary potential depth, which decreased with increasing target mass. Notably, the real potential depth was found to be identical for projectiles, resulting in a smaller volume integral for 7Li. Additionally, the imaginary volume integral was smaller for 7Li than for 6Li, indicating weaker absorption for 7Li.
In a complementary study, Y. Xu et al. [17] proposed a global phenomenological optical model (OM) potential for 7Li projectiles, based on elastic scattering ADs and reaction cross-section (σR) data for target nuclei ranging from 27Al to 208Pb at energies below 200 MeV. This potential provided satisfactory descriptions of 7Li elastic scattering across the studied systems. Microscopic approaches have also contributed significantly to our understanding. Xu and Pang [18] introduced a global potential by analyzing ADs from 6,7Li elastic scattering off targets (A ≥ 40) at Elab = 5–40 MeV/u. The single-folding model, incorporating the JLMB nucleon-nucleus interaction [21, 22] provided good agreement with experimental σR and ADs data. In a more fundamental approach, Chen et al. [19] developed a microscopic OP for 7Li+nucleus systems without adjustable parameters. This potential was constructed by folding the microscopic OP of 7Li's constituent nucleons over their density distributions, with the internal wave function described using the harmonic oscillator shell model. The resulting potential successfully predicted ADs and σR for targets ranging from A = 27 to 208 at energies below 450 MeV, demonstrating comparable performance to that of global phenomenological potentials. Basak et al. [20] provided additional insights through their analysis of elastic scattering cross sections and VAP for 6,7Li scattered from 12C, 26Mg, 58Ni, and 120Sn nuclei. Their OM calculations employed a real folded potential based on realistic two-nucleon interactions, requiring no normalization, along with imaginary and spin-orbit potentials. This approach successfully accounted for both cross section and VAPs, including the explanation of opposite signs observed in VAP data for 6,7Li + 58Ni and 6,7Li + 120Sn systems at Elab = 20 and 44 MeV, respectively.
This work presents a comprehensive investigation of elastic scattering cross sections for 7Li projectiles on 118,120Sn targets across a broad energy range. Utilizing multiple nuclear potential models and computational approaches, we systematically compare theoretical predictions with experimental data. A key focus of our analysis is the determination of the necessary normalization factors required to achieve optimal agreement with the ADs data for both 7Li + 118Sn and 7Li + 120Sn systems. The paper is structured as follows: Section II details the theoretical framework and potential models employed in our calculations, Section III presents and analyzes the results, and Section IV summarizes our principal findings and conclusions.
-
The elastic scattering ADs for the systems 7Li + 118Sn at Elab = 18.15–48 MeV and 7Li + 120Sn at Elab = 20–44 MeV have been reanalyzed using a systematic hierarchy of theoretical approaches. We begin with microscopic methods, including the São Paulo potential (SPP) and double-folding potentials (DFPs), advance to cluster folding potential (CFP) to explicitly account for the distinctive α + t configuration of 7Li, and ultimately employ the comprehensive continuum discretized coupled channels (CDCC) technique. This methodological progression provides complementary insights into the scattering dynamics and facilitates the identification of optimal interaction potentials that accurately reproduce the experimental ADs. The FRESCO code [23] was employed for the calculations, supplemented by SFRESCO extensions for χ2 minimization, which facilitated the accurate extraction of optimal potential parameters to fit the data.
-
The elastic scattering ADs for the systems 7Li + 118Sn at Elab = 18.15–48 MeV and 7Li + 120Sn at Elab = 20–44 MeV have been reanalyzed using a systematic hierarchy of theoretical approaches. We begin with microscopic methods, including the São Paulo potential (SPP) and double-folding potentials (DFPs), advance to cluster folding potential (CFP) to explicitly account for the distinctive α + t configuration of 7Li, and ultimately employ the comprehensive continuum discretized coupled channels (CDCC) technique. This methodological progression provides complementary insights into the scattering dynamics and facilitates the identification of optimal interaction potentials that accurately reproduce the experimental ADs. The FRESCO code [23] was employed for the calculations, supplemented by SFRESCO extensions for χ2 minimization, which facilitated the accurate extraction of optimal potential parameters to fit the data.
-
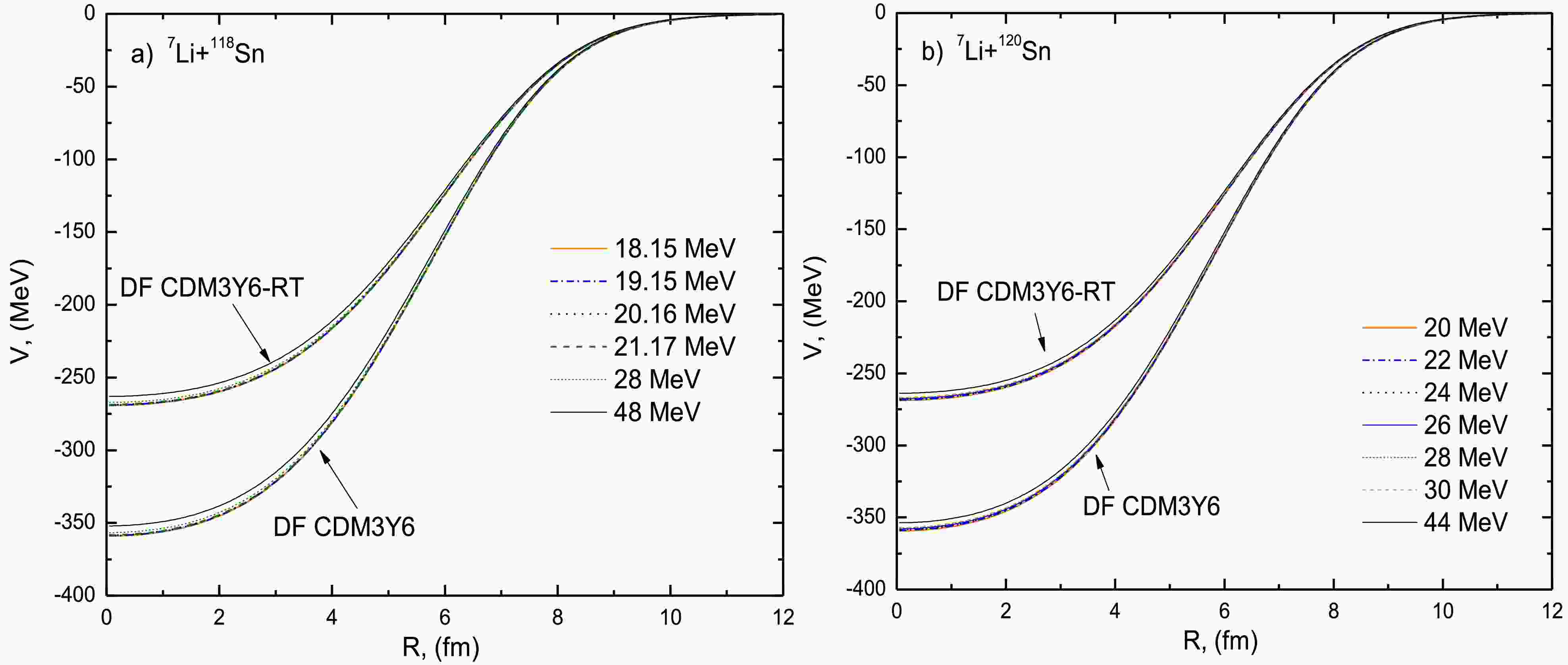
The São Paulo potential (SPP) offers a microscopically-based description of the nuclear interaction. This approach derives the potential through double-folding (DF) procedures that explicitly incorporate the nucleon-nucleon interaction potential (VNN) with realistic nuclear densities. The SPP formulation shares conceptual similarities with conventional DF potentials but maintains distinct advantages in its theoretical foundation. For the current analysis, the nuclear density distributions of 7Li and 118,120Sn were obtained from high-precision Dirac-Hartree-Bogoliubov (DHB) calculations, as tabulated by the REGINA code [24]. These microscopic densities provide a more rigorous basis for potential generation compared to phenomenological parameterizations. Figure 1 presents the complete set of derived SPPs for both systems across the investigated energy ranges. Within the SPP approach used here, the imaginary part of the potential is constructed to be proportional to the real part, sharing the same radial form factor, with a separate normalization factor.
-
The SPP offers a microscopic description of the nuclear interaction. This approach derives the potential through DF procedures that explicitly incorporate the nucleon-nucleon interaction potential (VNN) with realistic nuclear densities. The SPP formulation shares conceptual similarities with conventional DF potentials but maintains distinct advantages in its theoretical foundation. For the current analysis, the nuclear density distributions of 7Li and 118,120Sn were obtained from high-precision Dirac-Hartree-Bogoliubov (DHB) calculations, as tabulated by the REGINA code [24]. These microscopic densities provide a more rigorous basis for potential generation compared to phenomenological parameterizations. Figure 1 presents the complete set of derived SPPs for both systems across the investigated energy ranges. Within the SPP approach used here, the imaginary part of the potential is constructed to be proportional to the real part, sharing the same radial form factor, and with a separate normalization factor.
-
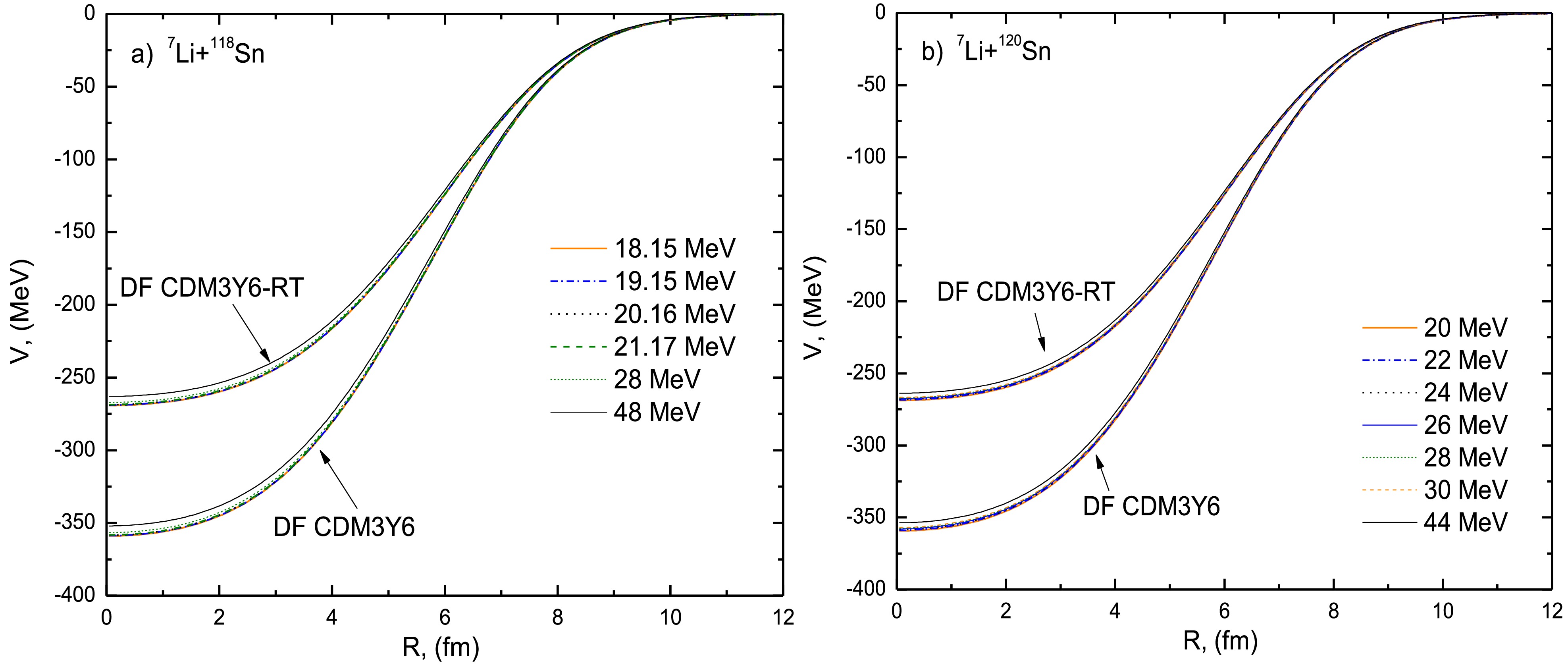
The 7Li + 118,120Sn systems were also investigated within the microscopic DF model using CDM3Y6 interactions. This analysis employed the same nuclear density distributions derived from the DHB model [24] as used in the SPP framework, ensuring consistency, while focusing specifically on the differences arising from the interaction potential. The DFMSPH code [25] generated the DFPs across the studied energy ranges by folding the projectile and target densities with the interaction potential (VNN):
$ V_{}^{DF}(R) = \int {\rho _p}{\text{(}}{r_p}{\text{) }}{\rho _t}{\text{(}}{r_t}{\text{) }}{V_{NN}}(s){\text{ }}{{\text{d}}^{\text{3}}}{r_p}{\text{ }}{{\text{d}}^{\text{3}}}{r_t}{\text{ , }}s = {r_t} - {r_p} + R. $

(1) The
$ {V_{NN}} $ (CDM3Y6 interaction) based on the M3Y-Paris potential incorporates both direct$ {v_{\text{D}}}(s) $ and exchange$ {v_{{\text{EX}}}}{\text{(}}s{\text{)}} $ components, which are density and energy- dependent:$ {v_{\text{D}}}_{({\text{EX}})}(\rho ,s) = F(\rho )g(E){v_{\text{D}}}_{({\text{EX}})}(s), $

(2) where s is the separation between two interacting nucleons and ρ is the nuclear matter density. This functional dependence accounts for the nuclear medium effects on the effective interaction, assuming the form [26]
$ F(\rho)=0.2658[1+3.8033\exp(-1.4099\rho)-4.0\rho]. $

(3) The energy-dependent factor
$ g(E) $ is expressed as [27]$ {g}\left({E}\right)=1-0.003({E}/{A}) g(E) = 1 - 0.003(E/A). $

(4) To explore additional physical effects, we implemented a modified version, CDM3Y6-RT, that incorporates the rearrangement term (RT) through an additional density-dependent correction
$ \Delta F(\rho ) $ [28]:$ \Delta F(\rho ) = 1.5\left[ {{\text{exp}}( - 0.833\rho ) - 1} \right]. $

(5) The rearrangement term
$ \Delta F(\rho ) $ accounts for the energy dependence arising from the variation in the single-nucleon potential with density, representing a correction due to the reorganization of the nuclear medium during the interaction. The direct and exchange components of the effective NN interaction are scaled by the modified density-dependent function$ \left[ {{F_{{\text{RT}}}}(\rho ) = \Delta F(\rho ) + F(\rho )} \right] $ before the folding integral is calculated. This results in a microscopically motivated, energy-dependent correction to the real part of the folded potential. The resulting CDM3Y6 and CDM3Y6-RT potential forms are displayed in Fig. 2. -
The 7Li + 118,120Sn systems were also investigated within the microscopic DF model using CDM3Y6 interactions. This analysis employed the same nuclear density distributions derived from the DHB model [24] as used in the SPP framework, ensuring consistency while focusing specifically on the differences arising from the interaction potential. The DFMSPH code [25] generated the DFPs across the studied energy ranges by folding the projectile and target densities with the interaction potential (VNN):
$ V_{}^{DF}(R) = \int {\rho _p}{\text{(}}{r_p}{\text{) }}{\rho _t}{\text{(}}{r_t}{\text{) }}{V_{NN}}(s){\text{ }}{{\text{d}}^{\text{3}}}{r_p}{\text{ }}{{\text{d}}^{\text{3}}}{r_t}{\text{ , }}s = {r_t} - {r_p} + R $

(1) The
$ {V_{NN}} $ (CDM3Y6 interaction) based on the M3Y-Paris potential, incorporates both direct$ {v_{\text{D}}}(s) $ and exchange$ {v_{{\text{EX}}}}{\text{(}}s{\text{)}} $ components, which are density- and energy- dependent:$ {v_{\text{D}}}_{({\text{EX}})}(\rho ,s) = F(\rho )g(E){v_{\text{D}}}_{({\text{EX}})}(s), $

(2) where s is the separation between two interacting nucleons and ρ is the nuclear matter density. This functional dependence accounts for the nuclear medium effects on the effective interaction, taking the form [26]:
$ F(\rho ) = 0.2658[1 + 3.8033\exp ( - 1.4099\rho ) - 4.0\rho ], $

(3) The energy-dependent factor
$ g(E) $ is expressed as [27]:$ \mathrm{g}\left(\mathrm{E}\right)=1-0.003(\mathrm{E}/\mathrm{A}) g(E) = 1 - 0.003(E/A) $

(4) To explore additional physical effects, we implemented a modified version, CDM3Y6-RT, which incorporates the rearrangement term (RT) through an additional density-dependent correction
$ \Delta F(\rho ) $ [28]:$ \Delta F(\rho ) = 1.5\left[ {{\text{exp}}( - 0.833\rho ) - 1} \right] $

(5) The rearrangement term
$ \Delta F(\rho ) $ accounts for the energy dependence arising from the variation of the single-nucleon potential with density, representing a correction due to the reorganization of the nuclear medium during the interaction. The direct and exchange components of the effective NN interaction are scaled by the modified density-dependent function$ \left[ {{F_{{\text{RT}}}}(\rho ) = \Delta F(\rho ) + F(\rho )} \right] $ before the folding integral is performed. This results in a microscopically motivated, energy-dependent correction to the real part of the folded potential. The resulting CDM3Y6 and CDM3Y6-RT potential forms are displayed in Fig. 2. -
The cluster folding model (CFM) formalism was specifically employed to incorporate the well-established α + t cluster configuration of the 7Li nuclei, which is particularly significant considering the modest binding energy of only 2.468 MeV. This approach constructs the effective potential through careful consideration of the individual α+target and t+target interactions, properly weighted by the cluster relative wave function
$ {{{\chi }}_{\alpha - t}}(r) $ as follows:$\begin{aligned}[b] {V^{CF}}(R) =\;& \int {} \Bigg[ {V_{{\text{ }}\alpha + {^{118}}{\text{Sn }}{{\text{(}}^{120}}{\text{Sn)}}}}\left( {R - \frac{{\text{3}}}{{\text{7}}}r} \right) \\&+ {V_{t{ + ^{118}}{\text{Sn}}{{\text{(}}^{120}}{\text{Sn)}}}}\left( {R + \frac{{\text{4}}}{{\text{7}}}r} \right) \Bigg]{\text{ }}{\left| {{{{\chi }}_{\alpha - t}}(r)} \right|^2}{\rm d}{\text{ }}r{\text{,}} \end{aligned}$

(6) $\begin{aligned}[b] {W^{CF}}(R) =\;& \int {} \Bigg[ {W_{{\text{ }}\alpha + {{\text{ }}^{118}}{\text{Sn}}{{\text{(}}^{120}}{\text{Sn)}}}}\left( {R - \frac{{\text{3}}}{{\text{7}}}r} \right)\\& + {W_{t{ + ^{118}}{\text{Sn}}{{\text{(}}^{120}}{\text{Sn)}}}}\left( {R + \frac{{\text{4}}}{{\text{7}}}r} \right) \Bigg]{\text{ }}{\left| {{{{\chi }}_{\alpha - t}}(r)} \right|^2}{\rm d}{\text{ }}r{\text{,}}\end{aligned} $

(7) where (
$ {V_{{\text{ }}\alpha + {{\text{ }}^{118}}{\text{Sn}}{{\text{(}}^{120}}{\text{Sn)}}}} $ ,$ {V_{t{ + ^{118}}{\text{Sn}}{{\text{(}}^{120}}{\text{Sn)}}}} $ ) and ($ {W_{{\text{ }}\alpha + {{\text{ }}^{118}}{\text{Sn}}{{\text{(}}^{120}}{\text{Sn)}}}} $ ,$ {W_{t{ + ^{118}}{\text{Sn}}{{\text{(}}^{120}}{\text{Sn)}}}} $ ) are the real and imaginary potentials for the α + 118Sn(120Sn) and t + 118Sn(120Sn) subsystems, respectively. These constituent potentials reproduce experimental data at energies Eα ≈ 4/7ELi and Et ≈ 3/7ELi. The α+t bound state (7Li ground state) is described by a 2P3/2 wave function generated from a WS potential with a radius of$0.667 \times \left( {{{\text{4}}^{{\text{1/3}}}} + {3^{1/3}}} \right) $ fm, diffuseness of 0.65 fm, and depth tuned to achieve the cluster binding energy. In this analysis, it was critical to select the appropriate constituent potentials. The 7Li + 118Sn analysis incorporated t + 118Sn potentials at 20 MeV [29] and α + 118Sn potentials at 27 MeV [30]. Similarly, the 7Li + 120Sn analysis incorporated t + 120Sn potentials at 20 MeV [29] and α + 120Sn potentials at 26.1 MeV [31], all carefully validated against existing experimental data. The complete set of derived CFPs is presented in Fig. 3.This multi-faceted theoretical framework enables a comprehensive investigation of the elastic scattering dynamics, systematically addressing the physical mechanisms influencing the interaction through increasingly sophisticated treatments of nuclear structure and reaction mechanisms. Each methodological approach provides complementary constraints on the potential forms and their parameters, collectively yielding a robust understanding of 7Li scattering processes.
-
The cluster folding model (CFM) formalism was specifically employed to incorporate the well-established α + t cluster configuration of 7Li nuclei, which is particularly significant given the modest binding energy of just 2.468 MeV. This approach constructs the effective potential through careful consideration of the individual α+target and t+target interactions, properly weighted by the cluster relative wave function
$ {{{\chi }}_{\alpha - t}}(r) $ as follows:$\begin{aligned}[b] {V^{CF}}(R) =\;& \int {} \Bigg[ {V_{{\text{ }}\alpha + {^{118}}{\text{Sn }}{{\text{(}}^{120}}{\text{Sn)}}}}\left( {R - \frac{{\text{3}}}{{\text{7}}}r} \right) \\&+ {V_{t{ + ^{118}}{\text{Sn}}{{\text{(}}^{120}}{\text{Sn)}}}}\left( {R + \frac{{\text{4}}}{{\text{7}}}r} \right) \Bigg]{\text{ }}{\left| {{{{\chi }}_{\alpha - t}}(r)} \right|^2}d{\text{ }}r{\text{,}} \end{aligned}$

(6) $\begin{aligned}[b] {W^{CF}}(R) =\;& \int {} \Bigg[ {W_{{\text{ }}\alpha + {{\text{ }}^{118}}{\text{Sn}}{{\text{(}}^{120}}{\text{Sn)}}}}\left( {R - \frac{{\text{3}}}{{\text{7}}}r} \right)\\& + {W_{t{ + ^{118}}{\text{Sn}}{{\text{(}}^{120}}{\text{Sn)}}}}\left( {R + \frac{{\text{4}}}{{\text{7}}}r} \right) \Bigg]{\text{ }}{\left| {{{{\chi }}_{\alpha - t}}(r)} \right|^2}d{\text{ }}r{\text{,}}\end{aligned} $

(7) where (
$ {V_{{\text{ }}\alpha + {{\text{ }}^{118}}{\text{Sn}}{{\text{(}}^{120}}{\text{Sn)}}}} $ and$ {V_{t{ + ^{118}}{\text{Sn}}{{\text{(}}^{120}}{\text{Sn)}}}} $ ) and ($ {W_{{\text{ }}\alpha + {{\text{ }}^{118}}{\text{Sn}}{{\text{(}}^{120}}{\text{Sn)}}}} $ and$ {W_{t{ + ^{118}}{\text{Sn}}{{\text{(}}^{120}}{\text{Sn)}}}} $ ) are the real and imaginary potentials for α + 118Sn(120Sn) and t + 118Sn(120Sn) subsystems, respectively. These constituent potentials reproduce experimental data at energies Eα ≈ 4/7ELi and Et ≈ 3/7ELi. The α+t bound state (7Li ground state) was described by a 2P3/2 wave function generated from a WS potential with a radius of$ {\text{0}}{\text{.677 x }}\left( {{{\text{4}}^{{\text{1/3}}}} + {3^{1/3}}} \right) $ fm, a diffuseness of 0.65 fm, and a depth tuned to achieve the cluster binding energy. Critical to this analysis was the selection of appropriate constituent potentials. The 7Li + 118Sn analysis incorporated t + 118Sn potentials at 20 MeV [29] and α + 118Sn potentials at 27 MeV [30]. Similarly, the 7Li + 120Sn analysis incorporated t + 120Sn potentials at 20 MeV [29] and α + 120Sn potentials at 26.1 MeV [31], all carefully validated against existing experimental data. The complete set of derived CFPs is presented in Fig. 3.This multi-faceted theoretical framework enables a comprehensive investigation of the elastic scattering dynamics, systematically addressing the physical mechanisms influencing the interaction through increasingly sophisticated treatments of nuclear structure and reaction mechanisms. Each methodological approach provides complementary constraints on the potential forms and their parameters, collectively yielding a robust understanding of 7Li scattering processes.
-
The elastic scattering ADs for the 7Li + 118Sn system at Elab = 18.15–48 MeV [4–6] and for the 7Li + 120Sn system at Elab = 20–44 MeV [7–9] were analyzed using the SPP, which provides a microscopic description of the nuclear interaction. Building upon the SPP2 formulation [32], we applied this approach to achieve a comprehensive description that incorporates the internal structure of the colliding nuclei. The real component of the potential was generated using the REGINA code framework, while the imaginary part was constructed as a scaled version of the real potential, maintaining a consistent radial dependence. The employed potential is given by
$ U(R) = {V_C}(R) - {N_{RSPP}}{\text{ }}{V^{DF}}(R) - {\rm i}{N_{ISPP}}{\text{ }}{V^{DF}}(R). $

(8) This formulation incorporates normalization factors for both real (NRSPP) and imaginary (NISPP) components. The optimized values of these factors provide important physical insights into the interaction dynamics. As detailed in Table 1, the analysis consistently requires significant reduction of the real potential strength, with average normalization factors of 0.54±0.28 for 118Sn and 0.60±0.05 for 120Sn. This substantial reduction—corresponding to approximately 46% and 40% weakening of the bare potential strength—directly reflects the impact of 7Li breakup on the elastic scattering channel. The energy dependence of these normalization factors is particularly pronounced near the Coulomb barrier region (VB ≈ 21 MeV), where coupling to breakup channels is most significant.
E
/MeVNRSPP NISPP χ2/N $ {\mathit{\sigma }}_{\mathit{R}} $ 

/mbJV
/MeV·fm3JW
/MeV·fm37Li + 118Sn 18.15 0.931 0.1 0.1 8.74 382.64 41.1 0.54 0.161 0.11 9.46 221.94 66.17 19.15 0.32 0.81 0.15 88.49 131.52 332.91 0.54 0.670 0.16 81.06 221.94 275.37 20.16 0.357 0.746 0.24 161.7 146.73 306.61 0.54 0.568 0.27 145.1 221.94 233.45 21.17 0.234 0.99 0.73 304.2 96.17 406.89 0.54 0.60 1.0 259.5 221.94 246.6 28 0.677 0.476 100.6 1037 278.25 195.64 0.54 0.363 118.2 958.6 221.94 149.19 48 0.734 0.624 2.5 2089 301.67 256.46 0.54 0.389 7.86 1927 221.94 159.88 7Li + 120Sn 20 0.602 0.426 1.8 122.8 251.46 177.94 0.6 0.427 1.9 122.9 250.2 178.36 22 0.632 0.414 4.1 355.3 263.99 172.93 0.6 0.477 6.51 366.2 250.2 199.24 24 0.617 0.56 29.2 653.1 257.72 233.91 0.6 0.57 30.3 652.0 250.2 238.09 26 0.502 0.43 21.3 810.9 209.69 179.61 0.6 0.62 50.8 896.6 250.2 258.97 28 0.631 0.565 68.6 1083 263.57 236.00 0.6 0.554 81.2 1072 250.2 231.41 30 0.631 0.439 100.1 1204 263.57 183.37 0.6 0.433 113.3 1193 250.2 180.86 44 0.563 0.464 0.04 1892 229.99 189.54 0.6 0.505 0.06 1892 250.2 210.94 Table 1. Optimal potential parameters for the 7Li + 118,120Sn nuclear system using SPP. The values of (JV), (JW), and (σR) are displayed. The underlined parameters are fixed.
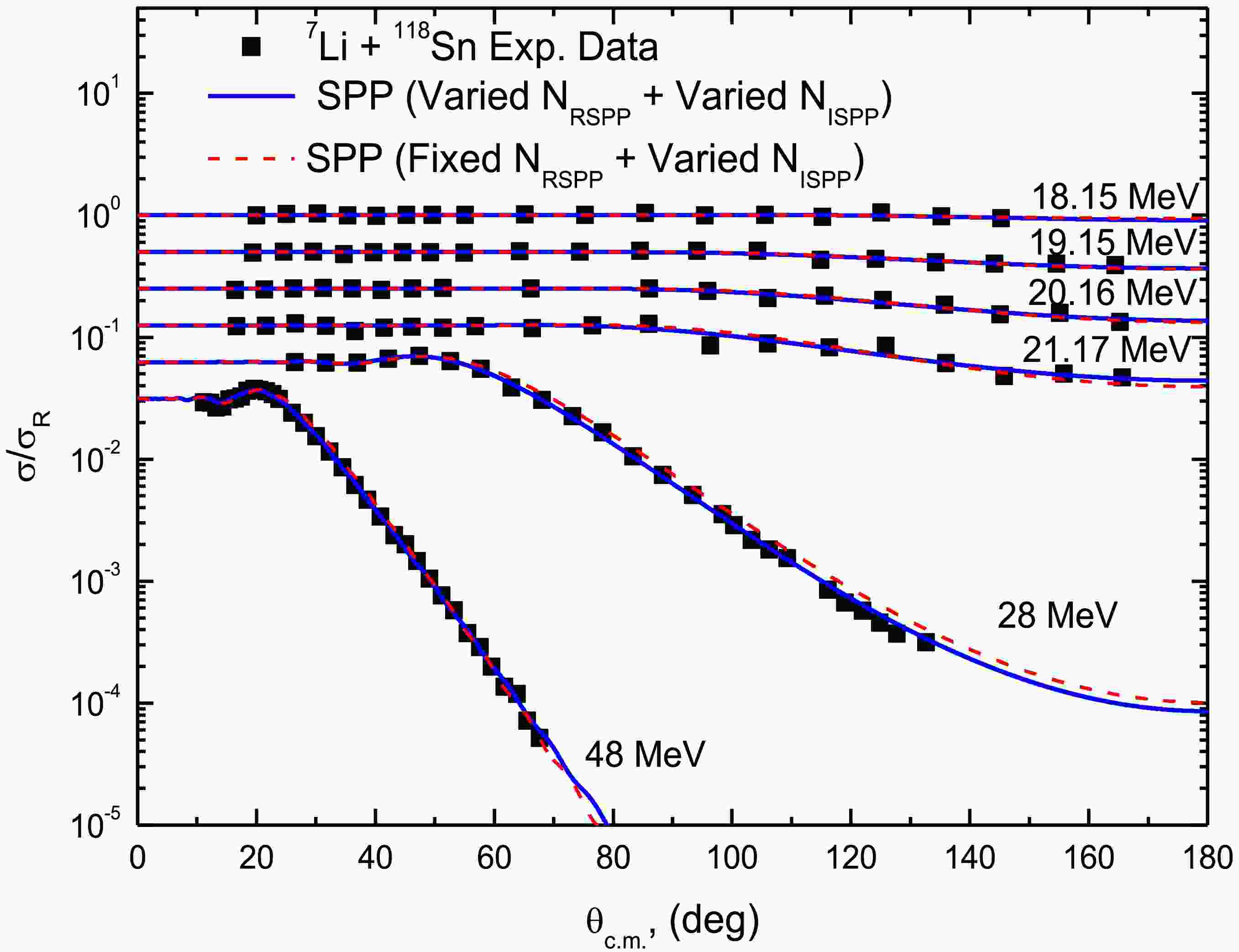
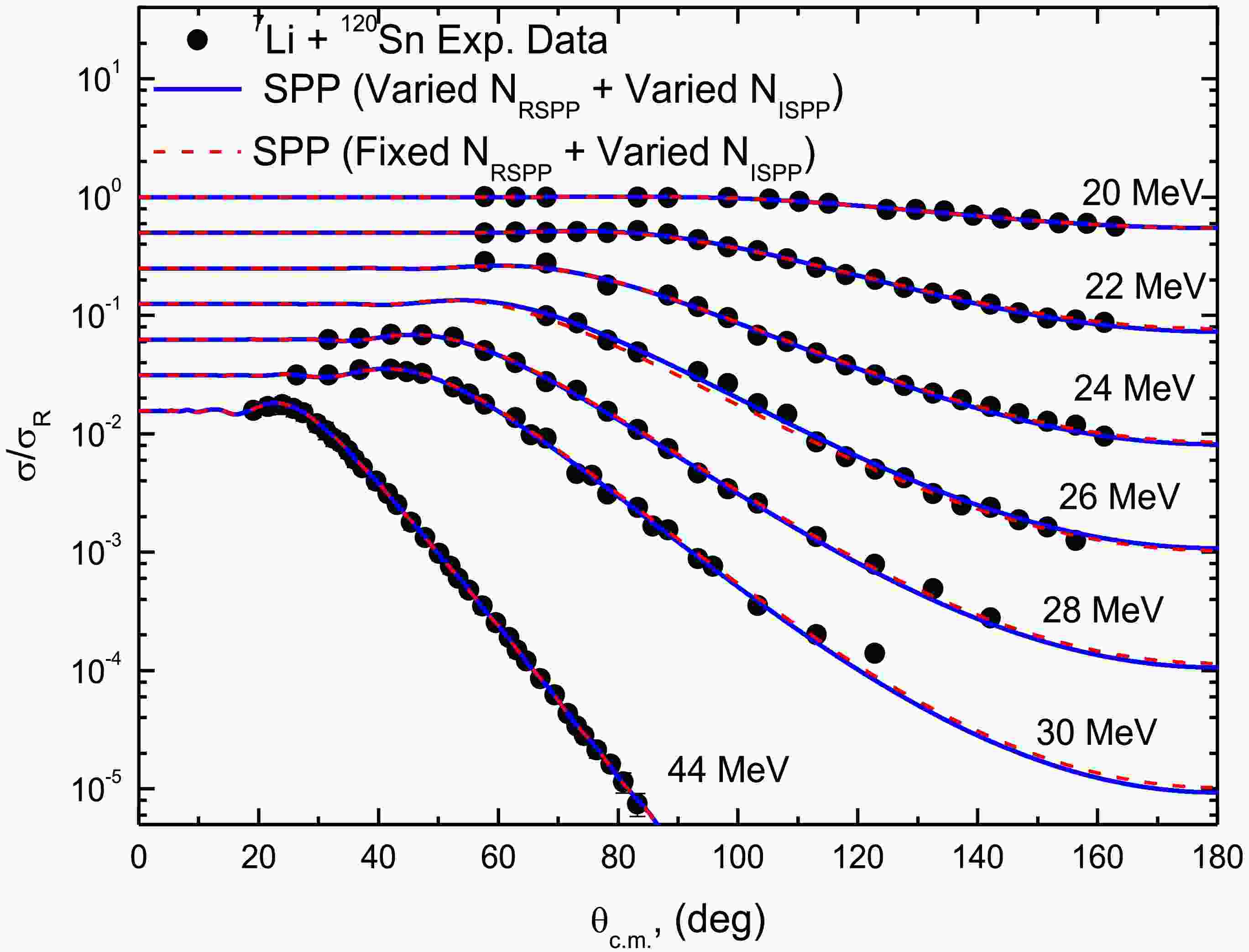
As shown in Figs. 4 and 5, this approach successfully reproduces the experimental ADs across the entire energy range. For clarity, the presented ADs are displaced by a factor of 0.5. The optimal potential parameters extracted from these fits are presented in Table 1, along with σR and the corresponding volume integrals (JV, JW). The systematic behavior of these parameters provides important insights into the energy dependence of the 7Li-nucleus interaction.

Figure 4. (color online) Experimental 118Sn (7Li,7Li)118Sn ADs (squares) versus SPP calculations (curves) at Elab= 18.15, 19.15, 20.16, 21.17, 28 and 48 MeV.
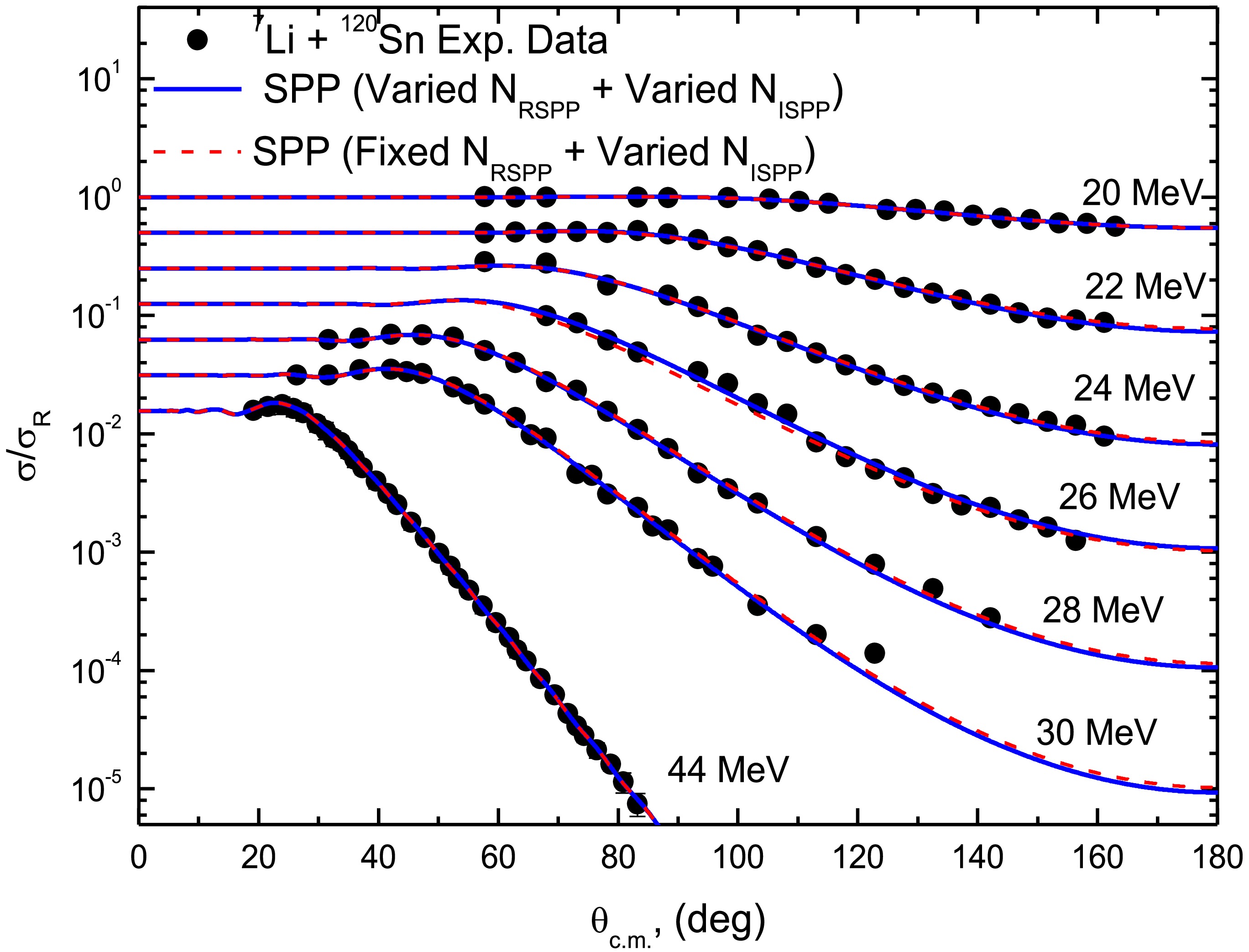
Figure 5. (color online) Experimental 120Sn(7Li,7Li)120Sn ADs (circles) versus SPP calculations (curves) at Elab= 20, 22, 24, 26, 28, 30 and 44 MeV.
Additionally, we reproduced the 7Li + 118,120Sn ADs using only one adjustable parameter (NISPP), fixing NRSPP at the aforementioned average normalization factors of (0.54 for 118Sn) and (0.60 for 120Sn). These results, presented as dashed curves in Figs. 4 and 5, agree well with the data. The optimal extracted NISPP values are listed in Table 1. The volume integrals derived from the SPP analyses using both the (varied NRSPP + varied NISPP) and (fixed NRSPP + varied NISPP) approaches exhibit behavior that is consistent with the breakup threshold anomaly (BTA) [33, 34]. This phenomenon, observed in scattering involving WB nuclei, is characterized by a decrease in the real potential strength (revealing a repulsive polarization potential) and an increase in the imaginary strength (enhanced absorption) as the energy approaches the Coulomb barrier. This contrasts with the normal threshold anomaly [35] observed with tightly bound nuclei. This systematic behavior emerges naturally from the microscopic foundation of the SPP. The success of this analysis highlights the manner in which the SPP framework incorporates the essential physics of WB projectile scattering, while maintaining a fundamental connection to microscopic nuclear structure. The required potential normalizations quantitatively capture the dynamic polarization effects from coupling to the breakup channel.
-
The elastic scattering ADs for the 7Li + 118Sn system at Elab = 18.15–48 MeV [4–6], and for the 7Li + 120Sn system at Elab = 20–44 MeV [7–9] were analyzed using the SPP, which provides a microscopically-based description of the nuclear interaction. Building upon the SPP2 formulation [32], we applied this approach to achieve a comprehensive description that incorporates the internal structure of the colliding nuclei. The real component of the potential was generated using the REGINA code framework, while the imaginary part was constructed as a scaled version of the real potential, maintaining a consistent radial dependence. The employed potential is:
$ U(R) = {V_C}(R) - {N_{RSPP}}{\text{ }}{V^{DF}}(R) - i{N_{ISPP}}{\text{ }}{V^{DF}}(R) $

(8) This formulation incorporates normalization factors for both real (NRSPP) and imaginary (NISPP) components. The optimized values of these factors provide important physical insights into the interaction dynamics. As detailed in Table I, the analysis consistently requires significant reduction of the real potential strength, with average normalization factors of 0.54±0.28 for 118Sn and 0.60±0.05 for 120Sn. This substantial reduction—corresponding to approximately 46% and 40% weakening of the bare potential strength— directly reflects the impact of 7Li breakup on the elastic scattering channel. The energy dependence of these normalization factors is particularly pronounced near the Coulomb barrier region (VB ≈ 21 MeV), where coupling to breakup channels is most significant.
As shown in Figs. 4 and 5, this approach successfully reproduced the experimental ADs across the entire energy range. For clarity, the presented ADs are displaced by a factor of 0.5. The optimal potential parameters extracted from these fits are presented in Table I, along with σR and the corresponding volume integrals (JV, JW). The systematic behavior of these parameters provides important insights into the energy dependence of the 7Li-nucleus interaction.

Figure 4. (color online) Experimental 118Sn (7Li,7Li)118Sn ADs (squares) versus SPP calculations (curves) at Elab= 18.15, 19.15, 20.16, 21.17, 28 and 48 MeV.

Figure 5. (color online) Experimental 120Sn(7Li,7Li)120Sn ADs (circles) versus SPP calculations (curves) at Elab= 20, 22, 24, 26, 28, 30 and 44 MeV.
Additionally, we reproduced the 7Li + 118,120Sn ADs using only one adjustable parameter (NISPP), fixing NRSPP at the aforementioned average normalization factors of (0.54 for 118Sn) and (0.60 for 120Sn). These results, presented as dashed curves in Figs. 4 and 5, agree well with the data. The optimal extracted NISPP values are listed in Table 1. The derived volume integrals from the SPP analyses using both (varied NRSPP + varied NISPP) and (fixed NRSPP + varied NISPP) approaches exhibit behavior consistent with the breakup threshold anomaly (BTA) [33, 34]. This phenomenon, observed in scattering involving WB nuclei, is characterized by a decrease in the real potential strength (revealing a repulsive polarization potential) and an increase in the imaginary strength (enhanced absorption) as the energy approaches the Coulomb barrier. This contrasts with the normal threshold anomaly [35] seen with tightly bound nuclei. This systematic behavior emerges naturally from the microscopic foundation of the SPP. The success of this analysis highlights how the SPP framework incorporates the essential physics of WB projectile scattering while maintaining a fundamental connection to microscopic nuclear structure. The required potential normalizations quantitatively capture the dynamic polarization effects from coupling to the breakup channel.
E
(MeV)NRSPP NISPP χ2/N $ {\mathit{\sigma }}_{\mathit{R}} $ 

(mb)JV
(MeV·fm3)JW
(MeV·fm3)7Li + 118Sn 18.15 0.931 0.1 0.1 8.74 382.64 41.1 0.54 0.161 0.11 9.46 221.94 66.17 19.15 0.32 0.81 0.15 88.49 131.52 332.91 0.54 0.670 0.16 81.06 221.94 275.37 20.16 0.357 0.746 0.24 161.7 146.73 306.61 0.54 0.568 0.27 145.1 221.94 233.45 21.17 0.234 0.99 0.73 304.2 96.17 406.89 0.54 0.60 1.0 259.5 221.94 246.6 28 0.677 0.476 100.6 1037 278.25 195.64 0.54 0.363 118.2 958.6 221.94 149.19 48 0.734 0.624 2.5 2089 301.67 256.46 0.54 0.389 7.86 1927 221.94 159.88 7Li + 120Sn 20 0.602 0.426 1.8 122.8 251.46 177.94 0.6 0.427 1.9 122.9 250.2 178.36 22 0.632 0.414 4.1 355.3 263.99 172.93 0.6 0.477 6.51 366.2 250.2 199.24 24 0.617 0.56 29.2 653.1 257.72 233.91 0.6 0.57 30.3 652.0 250.2 238.09 26 0.502 0.43 21.3 810.9 209.69 179.61 0.6 0.62 50.8 896.6 250.2 258.97 28 0.631 0.565 68.6 1083 263.57 236.00 0.6 0.554 81.2 1072 250.2 231.41 30 0.631 0.439 100.1 1204 263.57 183.37 0.6 0.433 113.3 1193 250.2 180.86 44 0.563 0.464 0.04 1892 229.99 189.54 0.6 0.505 0.06 1892 250.2 210.94 Table 1. Optimal potential parameters for 7Li + 118,120Sn nuclear system using SPP. The values of (JV), (JW), and (σR) are displayed. Underlined parameters mean fixed.
-
We further investigated the 7Li + 118,120Sn systems using the microscopic DF model with CDM3Y6 interactions, with and without the rearrangement term (RT). The comparison between standard CDM3Y6 and CDM3Y6-RT results offers valuable insights into the importance of rearrangement effects in these scattering systems. The systematic differences between these approaches help quantify how such microscopic corrections influence the overall potential strength and energy dependence required to reproduce the experimental ADs. The employed central is:
$ U(R) = {V_C}(R) - {N_{RDF}}{\text{ }}{V^{DF}}(R) - i{N_{IDF}}{\text{ }}{V^{DF}}(R) $

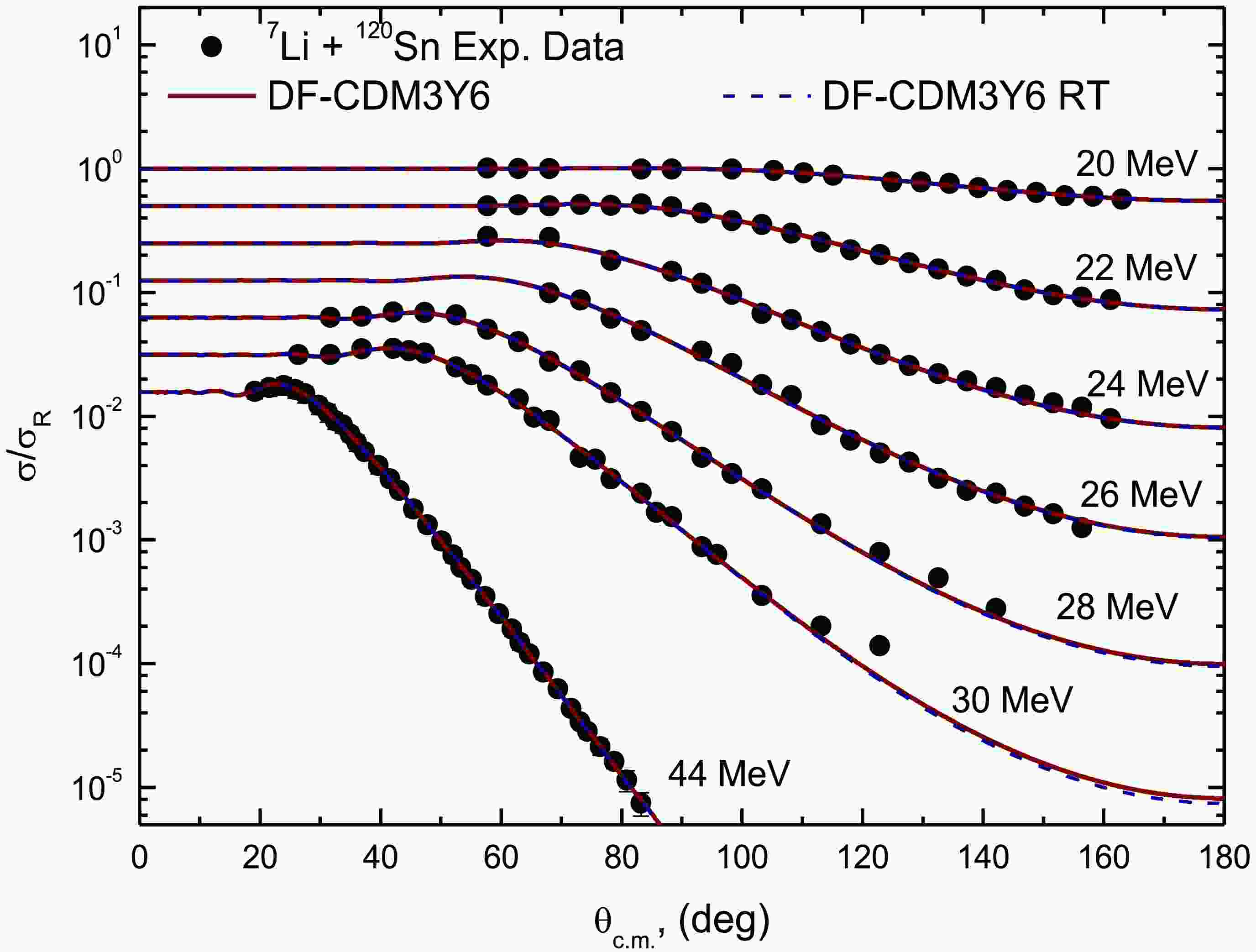
(9) The analysis introduced two adjustable parameters: NRDF and NIDF as normalization for the real and imaginary potential components respectively. The imaginary component of the potential is generated by scaling the real folded potential. The DFP calculations using the CDM3Y6 interaction successfully reproduce the experimental ADs for 7Li + 118,120Sn systems, as evidenced by the good agreement depicted in Figs. 6 and 7. The best fit NRDF and NIDF parameters derived from the analyses (Table 2) provide key insights into the underlying interaction dynamics. For the 7Li + 118Sn system, the real DF potential strength requires substantial reduction with an average NRDF value of 0.35 ± 0.19, corresponding to approximately 65% weakening of the bare potential. The 7Li + 120Sn system shows a similar but somewhat less pronounced effect, with an average NRDF of 0.41 ± 0.03. The inclusion of the rearrangement term through the CDM3Y6-RT modification yields comparable quality fits (Figs. 6 and 7), with only marginal differences in the required normalization. The 7Li + 118Sn system now shows an average NRDF of 0.37 ± 0.20 (63% reduction), while the 7Li + 120Sn system yields 0.422 ± 0.03 (58% reduction). The minimal variation between standard CDM3Y6 and CDM3Y6-RT results suggests that rearrangement effects play a secondary role compared to the dominant breakup dynamics in these systems.

Figure 6. (color online) Experimental between 118Sn(7Li,7Li)118Sn ADs (squares) versus DF calculations utilizing both CDM3Y6 (curves) and CDM3Y6-RT interactions (dashed curves) at Elab= 18.15, 19.15, 20.16, 21.17, 28 and 48 MeV.
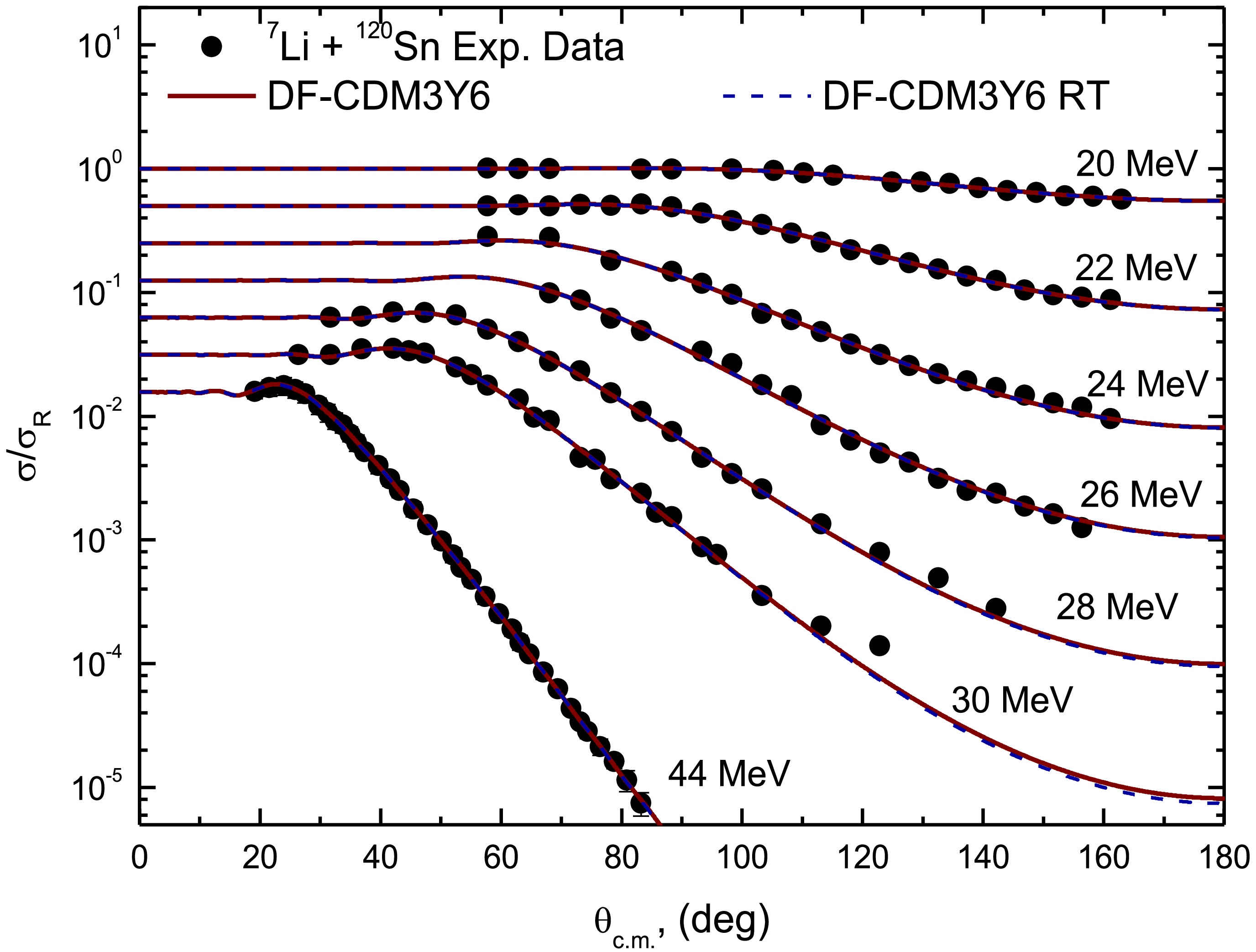
Figure 7. (color online) Experimental 120Sn(7Li,7Li)120Sn ADs (circles) versus DF calculations utilizing both CDM3Y6 (curves) and CDM3Y6-RT interactions (dashed curves) at Elab= 20, 22, 24, 26, 28, 30 and 44 MeV.
E (MeV) Interaction model NRDF NIDF χ2/N $ {\mathit{\sigma }}_{\mathit{R}} $ (mb)

JV (MeV·fm3) JW (MeV·fm3) 7Li + 118Sn 18.15 CDM3Y6 0.585 0.1 0.1 10.46 256.90 43.92 CDM3Y6-RT 0.623 0.215 0.1 10.19 221.10 76.30 19.15 CDM3Y6 0.221 0.549 0.15 88.49 96.964 240.87 CDM3Y6-RT 0.228 0.568 0.15 88.57 80.83 201.37 20.16 CDM3Y6 0.244 0.51 0.24 161.9 106.97 223.58 CDM3Y6-RT 0.252 0.531 0.24 162.1 89.25 188.07 21.17 CDM3Y6 0.1 0.765 0.71 320.1 43.75 334.69 CDM3Y6-RT 0.1 0.797 0.71 320.3 35.38 281.98 28 CDM3Y6 0.458 0.353 89.4 1044 199.44 153.71 CDM3Y6-RT 0.477 0.386 84.3 1048 167.71 135.72 48 CDM3Y6 0.498 0.48 2.3 2115 213.20 205.49 CDM3Y6-RT 0.524 0.536 2.3 2128 181.01 185.15 7Li + 120Sn 20 CDM3Y6 0.415 0.293 1.8 122.8 182.14 128.60 CDM3Y6-RT 0.431 0.307 1.8 123.0 152.96 108.95 22 CDM3Y6 0.43 0.295 4.2 357.0 188.40 129.25 CDM3Y6-RT 0.447 0.316 4.3 358.5 158.34 111.93 24 CDM3Y6 0.414 0.404 30.69 657.9 181.08 176.70 CDM3Y6-RT 0.428 0.436 31.6 661.0 151.34 154.17 26 CDM3Y6 0.338 0.316 20.5 817.8 147.54 137.93 CDM3Y6-RT 0.351 0.345 20.0 822.2 123.87 121.75 28 CDM3Y6 0.423 0.409 73.2 1089 184.38 178.27 CDM3Y6-RT 0.439 0.442 76.4 1092 154.64 155.70 30 CDM3Y6 0.427 0.321 99.6 1210 185.41 139.38 CDM3Y6-RT 0.447 0.349 99.8 1213 157.17 122.72 44 CDM3Y6 0.39 0.375 0.03 1931 167.66 161.21 CDM3Y6-RT 0.414 0.431 0.03 1953 143.77 149.68 Table 2. Optimized parameters for the 7Li + 118,120Sn systems using DF-CDM3Y6 interactions with/without RT, showing fitted NRDF and NIDF values with corresponding JV, JW, and σR results.
-
We further investigated the 7Li + 118,120Sn systems using the microscopic DF model with CDM3Y6 interactions, with and without the rearrangement term (RT). The comparison between the standard CDM3Y6 and CDM3Y6-RT results offers valuable insights into the importance of rearrangement effects in these scattering systems. The systematic differences between these approaches help quantify the mechanism by which such microscopic corrections influence the overall potential strength and energy dependence required to reproduce the experimental ADs. The employed central is
$ U(R) = {V_C}(R) - {N_{RDF}}{\text{ }}{V^{DF}}(R) - {\rm i}{N_{IDF}}{\text{ }}{V^{DF}}(R). $

(9) The analysis introduces two adjustable parameters: NRDF and NIDF as normalization for the real and imaginary potential components, respectively. The imaginary component of the potential is generated by scaling the real folded potential. The DFP calculations using the CDM3Y6 interaction successfully reproduce the experimental ADs for the 7Li + 118,120Sn system, as evidenced by the good agreement depicted in Figs. 6 and 7. The best fit NRDF and NIDF parameters derived from the analyses (Table 2) provide key insights into the underlying interaction dynamics. For the 7Li + 118Sn system, the real DF potential strength requires substantial reduction with an average NRDF value of 0.35 ± 0.19, corresponding to approximately 65% weakening of the bare potential. The 7Li + 120Sn system shows a similar, but somewhat less pronounced effect, with an average NRDF of 0.41 ± 0.03. The inclusion of the rearrangement term through the CDM3Y6-RT modification yields comparable quality fits (Figs. 6 and 7), with only marginal differences in the required normalization. The 7Li + 118Sn system now shows an average NRDF of 0.37 ± 0.20 (63% reduction), while the 7Li + 120Sn system yields 0.422 ± 0.03 (58% reduction). The minimal variation between the standard CDM3Y6 and CDM3Y6-RT results suggests that rearrangement effects play a secondary role compared to the dominant breakup dynamics in these systems.

Figure 6. (color online) Experimental between 118Sn(7Li,7Li) 118Sn ADs (squares) versus DF calculations utilizing both CDM3Y6 (curves) and CDM3Y6-RT interactions (dashed curves) at Elab= 18.15, 19.15, 20.16, 21.17, 28 and 48 MeV.

Figure 7. (color online) Experimental 120Sn(7Li,7Li)120Sn ADs (circles) versus DF calculations utilizing both CDM3Y6 (curves) and CDM3Y6-RT interactions (dashed curves) at Elab= 20, 22, 24, 26, 28, 30 and 44 MeV.
E /MeV Interaction model NRDF NIDF χ2/N $ {\mathit{\sigma }}_{\mathit{R}} $ /mb

JV/MeV·fm3 JW /MeV·fm3 7Li + 118Sn 18.15 CDM3Y6 0.585 0.1 0.1 10.46 256.90 43.92 CDM3Y6-RT 0.623 0.215 0.1 10.19 221.10 76.30 19.15 CDM3Y6 0.221 0.549 0.15 88.49 96.964 240.87 CDM3Y6-RT 0.228 0.568 0.15 88.57 80.83 201.37 20.16 CDM3Y6 0.244 0.51 0.24 161.9 106.97 223.58 CDM3Y6-RT 0.252 0.531 0.24 162.1 89.25 188.07 21.17 CDM3Y6 0.1 0.765 0.71 320.1 43.75 334.69 CDM3Y6-RT 0.1 0.797 0.71 320.3 35.38 281.98 28 CDM3Y6 0.458 0.353 89.4 1044 199.44 153.71 CDM3Y6-RT 0.477 0.386 84.3 1048 167.71 135.72 48 CDM3Y6 0.498 0.48 2.3 2115 213.20 205.49 CDM3Y6-RT 0.524 0.536 2.3 2128 181.01 185.15 7Li + 120Sn 20 CDM3Y6 0.415 0.293 1.8 122.8 182.14 128.60 CDM3Y6-RT 0.431 0.307 1.8 123.0 152.96 108.95 22 CDM3Y6 0.43 0.295 4.2 357.0 188.40 129.25 CDM3Y6-RT 0.447 0.316 4.3 358.5 158.34 111.93 24 CDM3Y6 0.414 0.404 30.69 657.9 181.08 176.70 CDM3Y6-RT 0.428 0.436 31.6 661.0 151.34 154.17 26 CDM3Y6 0.338 0.316 20.5 817.8 147.54 137.93 CDM3Y6-RT 0.351 0.345 20.0 822.2 123.87 121.75 28 CDM3Y6 0.423 0.409 73.2 1089 184.38 178.27 CDM3Y6-RT 0.439 0.442 76.4 1092 154.64 155.70 30 CDM3Y6 0.427 0.321 99.6 1210 185.41 139.38 CDM3Y6-RT 0.447 0.349 99.8 1213 157.17 122.72 44 CDM3Y6 0.39 0.375 0.03 1931 167.66 161.21 CDM3Y6-RT 0.414 0.431 0.03 1953 143.77 149.68 Table 2. Optimized parameters for the 7Li + 118,120Sn systems using DF-CDM3Y6 interactions with/without RT, showing the fitted NRDF and NIDF values with corresponding JV, JW, and σR results.
-
The remarkable clusterization tendency of 7Li, particularly its preferential dissociation into t + α configuration at ~ 2.468 MeV, motivates our application of the CFP approach within the microscopic CFM framework. This method effectively reproduces the 7Li + 118,120Sn ADs via the following central potential formulation:
$ U(R) = {V_C}(R) - {N_{RCF}}{\text{ }}{V^{CF}}(R) - i{\text{ }}{N_{ICF}}{\text{ }}{W^{CF}}(R) $

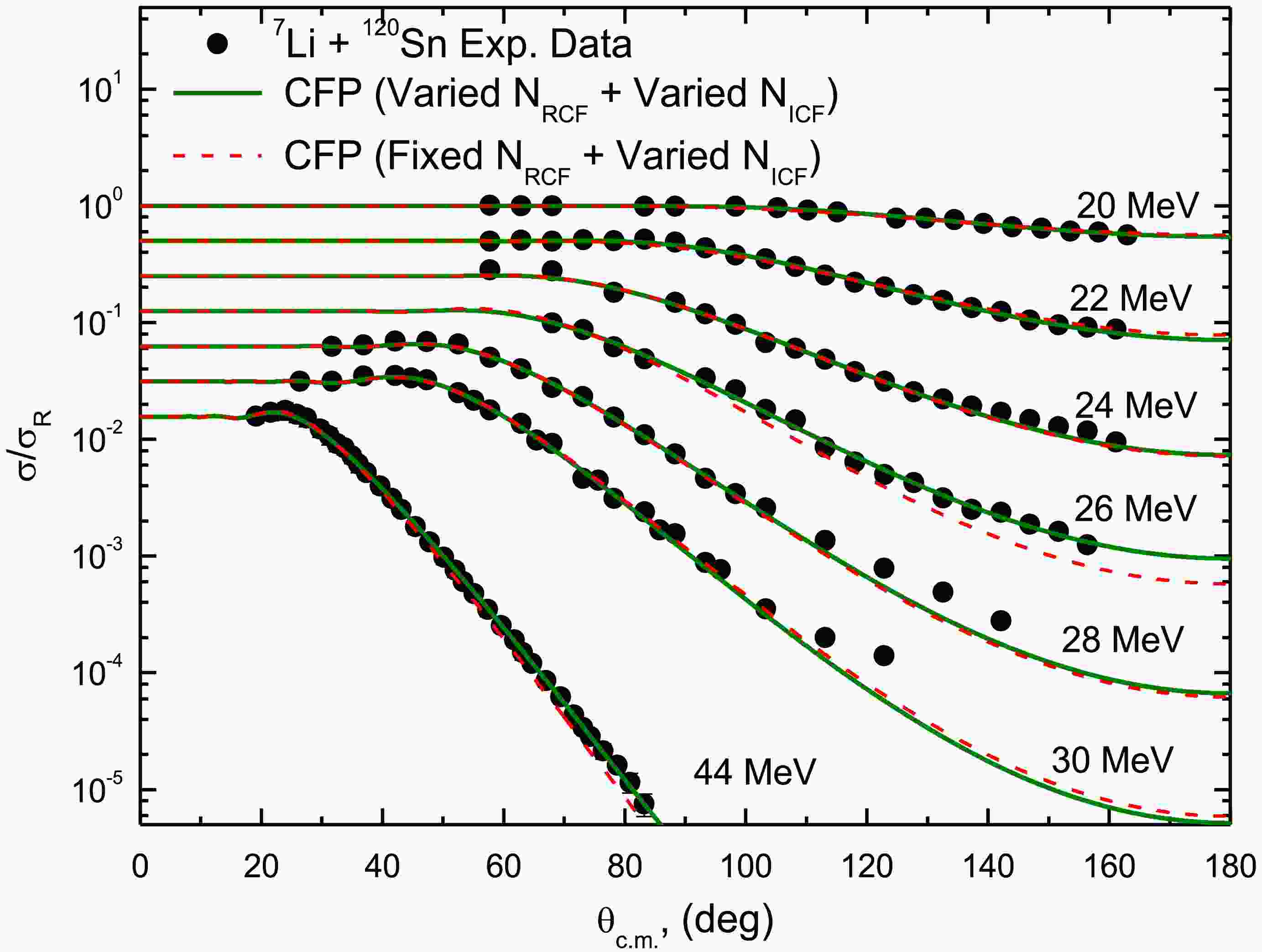
(10) The 7Li + 118,120Sn ADs were reproduced using two parameters: NRCF (real CFP normalization) and NICF (imaginary CFP normalization). The CFP based calculations successfully reproduced the 7Li + 118,120Sn ADs across all measured energies and angular range, as demonstrated in Figs. 8 and 9. Excellent agreement is achieved overall, though the higher χ2 values observed at 28 and 48 MeV for 118Sn and at 28 and 30 MeV for 120Sn originate from minor discrepancies at backward angles (θ > 110°). These deviations likely arise from other reaction channels, not accounted for in the double and cluster folding calculations, that become significant at these energies and angles.
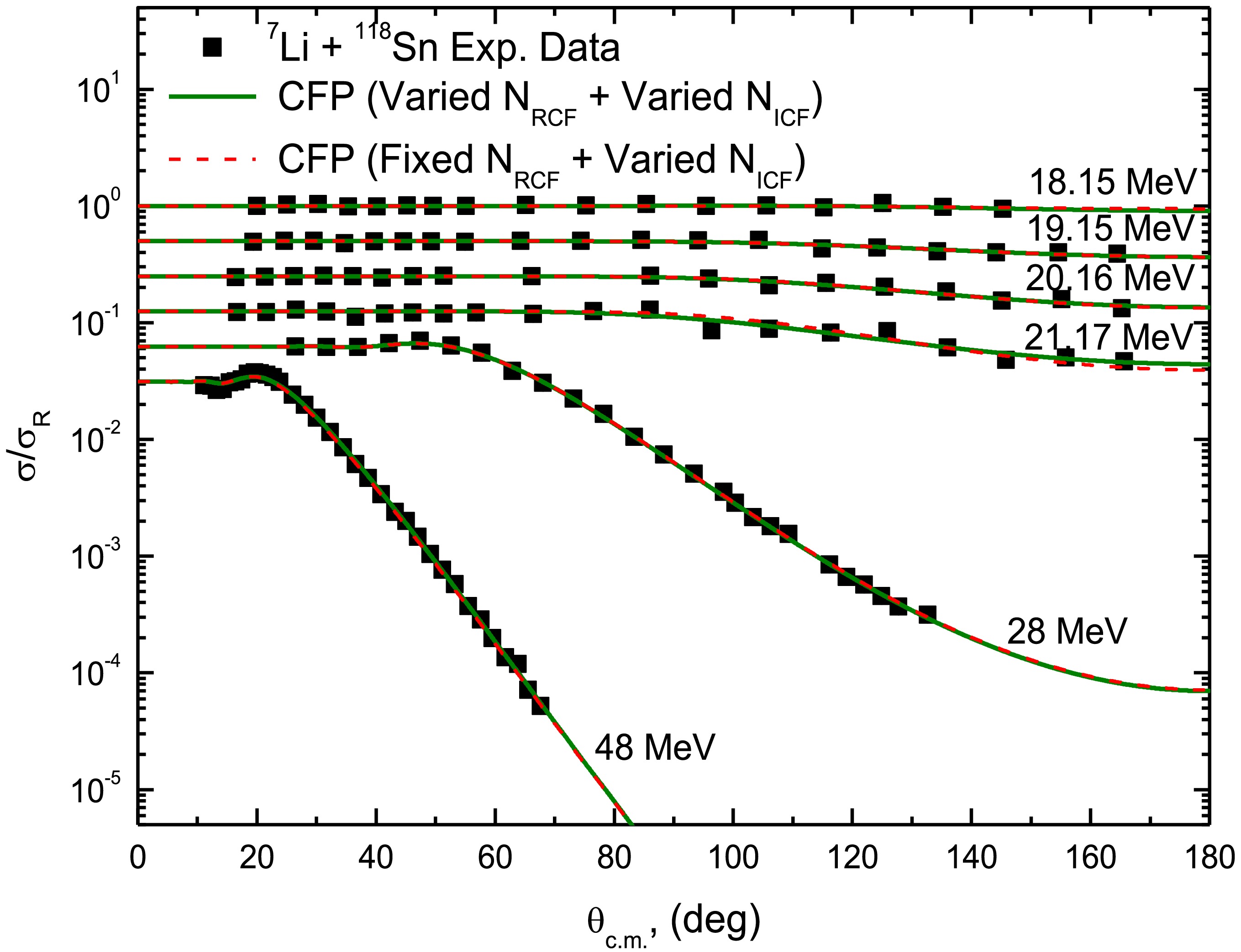
Figure 8. (color online) Experimental 118Sn(7Li,7Li)118Sn ADs at Elab= 18.15, 19.15, 20.16, 21.17, 28 and 48 MeV (squares) compared to the CFP calculations (curves).

Figure 9. (color online) Experimental 120Sn(7Li,7Li)120Sn ADs at Elab= 20, 22, 24, 26, 28, 30 and 44 MeV (circles) compared to the CFP calculations (curves).
The analysis within CFP framework reveals NRCF values of 0.50 ± 0.23 and 0.40 ± 0.09 for 7Li + 118Sn and 7Li + 120Sn systems, respectively (Table 3), corresponding to ~ 50 % and 60 % reductions in real CFP strength. This consistent reduction requirement mirrors our observations in SPP, DF-CDM3Y6, and DF-CDM3Y6-RT analyses, creating a coherent picture across different theoretical approaches. This consistency strongly suggests that the required normalization primarily reflects dynamic polarization effects arising from 7Li's weak binding and cluster nature, rather than being an artifact of any particular model [36-41]. The slightly greater reduction observed for 120Sn compared to 118Sn may indicate subtle mass-dependent variations in how the breakup process modifies the effective potential, though both systems clearly demonstrate the characteristic signatures of WB projectile scattering [36-40]. These results collectively highlight how the CFM provides both quantitative agreement with experimental data and valuable physical insight into the underlying reaction mechanisms. By treating the α and t components explicitly, the approach captures essential features of the 7Li-nucleus interaction that more phenomenological treatments might obscure.
E
(MeV)NRCF NICF χ2/N $ {\mathit{\sigma }}_{\mathit{R}} $ 

(mb)JV
(MeV·fm3)JW
(MeV·fm3)7Li + 118Sn 18.15 0.905 0.1 0.1 11.10 297.87 6.77 0.5 0.108 0.11 9.81 164.58 7.31 19.15 0.502 0.581 0.17 93.62 165.23 39.33 0.5 0.581 0.17 93.56 164.58 39.33 20.16 0.435 0.638 0.23 172.1 143.18 43.19 0.5 0.580 0.23 163.8 164.58 39.27 21.17 0.192 0.99 0.7 338.3 63.19 67.02 0.5 0.607 1.0 272.5 164.58 41.09 28 0.505 0.788 104.8 1107 166.22 53.35 0.5 0.793 105.4 1108 164.58 53.69 48 0.455 1.355 3.6 2293 149.76 91.73 0.5 1.49 4.6 2342 164.58 100.87 7Li + 120Sn 20 0.545 0.368 1.4 131.2 158.58 25.89 0.4 0.510 3.4 153.8 116.38 35.88 22 0.475 0.492 5.6 385.1 138.22 34.61 0.4 0.647 13.5 421.3 116.38 45.52 24 0.391 0.732 50.2 708.7 113.77 51.50 0.4 0.708 50.4 702.5 116.38 49.81 26 0.294 0.696 17.16 896.6 85.548 48.96 0.4 0.544 81.16 864.5 116.38 38.27 28 0.384 0.781 151.7 1150 111.74 54.94 0.4 0.756 154.8 1144 116.38 53.18 30 0.428 0.627 130.1 1263 124.54 44.11 0.4 0.671 140.2 1274 116.38 47.21 44 0.315 1.14 0.08 1892 91.66 80.20 0.4 0.99 1.89 2115 116.38 69.65 Table 3. Optimized parameters for the 7Li + 118,120Sn systems obtained from the calculations within CFP. The values of σR, JV, and JW are given. Underlined parameters mean fixed.
Moreover, we reproduced the 7Li + 118,120Sn ADs using one adjustable parameter, NICF, fixing the NRCF at the aforementioned average extracted normalizations (0.50 for 118Sn) and (0.40 for 120Sn). These results, presented as dashed curves in Figs. 8 and 9, agree well with the ADs data. The optimal extracted NICF values from both (varied NRCF + varied NICF) and (fixed NRCF + varied NICF) approaches are listed in Table 3. The extracted JW values show a non-vanishing nature below the barrier, a signature of the BTA phenomenon.
-
The remarkable clusterization tendency of 7Li, particularly its preferential dissociation into the t + α configuration at ~ 2.468 MeV, motivates our application of the CFP approach within the microscopic CFM framework. This method effectively reproduces the 7Li + 118,120Sn ADs by the following central potential formulation:
$ U(R) = {V_C}(R) - {N_{RCF}}{\text{ }}{V^{CF}}(R) - {\rm i}{\text{ }}{N_{ICF}}{\text{ }}{W^{CF}}(R). $

(10) The 7Li + 118,120Sn ADs were reproduced using two parameters: NRCF (real CFP normalization) and NICF (imaginary CFP normalization). The CFP based calculations successfully reproduced the 7Li + 118,120Sn ADs across all measured energies and the angular range, as demonstrated in Figs. 8 and 9. Excellent agreement was achieved overall; however, the higher χ2 values observed at 28 and 48 MeV for 118Sn and at 28 and 30 MeV for 120Sn originate from minor discrepancies at backward angles (θ > 110°). These deviations likely arise from other reaction channels and are not accounted for in the double and cluster folding calculations. They become significant at these energies and angles.

Figure 8. (color online) Experimental 118Sn(7Li,7Li)118Sn ADs at Elab= 18.15, 19.15, 20.16, 21.17, 28, and 48 MeV (squares) compared to the CFP calculations (curves).

Figure 9. (color online) Experimental 120Sn(7Li,7Li)120Sn ADs at Elab= 20, 22, 24, 26, 28, 30, and 44 MeV (circles) compared to the CFP calculations (curves).
The analysis within the CFP framework reveals NRCF values of 0.50 ± 0.23 and 0.40 ± 0.09 for 7Li + 118Sn and 7Li + 120Sn systems, respectively (Table 3), corresponding to ~50% and 60% reductions in the real CFP strength. This consistent reduction requirement mirrors our observations in the SPP, DF-CDM3Y6, and DF-CDM3Y6-RT analyses, creating a coherent picture across different theoretical approaches. This consistency strongly suggests that the required normalization primarily reflects dynamic polarization effects arising from the weak binding and cluster nature of 7Li, rather than being an artifact of any particular model [36−41]. The slightly greater reduction observed for 120Sn compared to 118Sn may indicate subtle mass-dependent variations in the modification of the effective potential by the breakup process; however, both systems clearly demonstrate the characteristic signatures of WB projectile scattering [36−40]. These results collectively highlight how the CFM provides both quantitative agreement with experimental data and valuable physical insight into the underlying reaction mechanisms. By treating the α and t components explicitly, the approach captures the essential features of the 7Li-nucleus interaction that might be obscured by more phenomenological treatments.
E
/MeVNRCF NICF χ2/N $ {\mathit{\sigma }}_{\mathit{R}} $ 

/mbJV
/MeV·fm3JW
/MeV·fm37Li + 118Sn 18.15 0.905 0.1 0.1 11.10 297.87 6.77 0.5 0.108 0.11 9.81 164.58 7.31 19.15 0.502 0.581 0.17 93.62 165.23 39.33 0.5 0.581 0.17 93.56 164.58 39.33 20.16 0.435 0.638 0.23 172.1 143.18 43.19 0.5 0.580 0.23 163.8 164.58 39.27 21.17 0.192 0.99 0.7 338.3 63.19 67.02 0.5 0.607 1.0 272.5 164.58 41.09 28 0.505 0.788 104.8 1107 166.22 53.35 0.5 0.793 105.4 1108 164.58 53.69 48 0.455 1.355 3.6 2293 149.76 91.73 0.5 1.49 4.6 2342 164.58 100.87 7Li + 120Sn 20 0.545 0.368 1.4 131.2 158.58 25.89 0.4 0.510 3.4 153.8 116.38 35.88 22 0.475 0.492 5.6 385.1 138.22 34.61 0.4 0.647 13.5 421.3 116.38 45.52 24 0.391 0.732 50.2 708.7 113.77 51.50 0.4 0.708 50.4 702.5 116.38 49.81 26 0.294 0.696 17.16 896.6 85.548 48.96 0.4 0.544 81.16 864.5 116.38 38.27 28 0.384 0.781 151.7 1150 111.74 54.94 0.4 0.756 154.8 1144 116.38 53.18 30 0.428 0.627 130.1 1263 124.54 44.11 0.4 0.671 140.2 1274 116.38 47.21 44 0.315 1.14 0.08 1892 91.66 80.20 0.4 0.99 1.89 2115 116.38 69.65 Table 3. Optimized parameters for the 7Li + 118,120Sn systems obtained from calculations within the CFP. The values of σR, JV, and JW are provided. The underlined parameters are fixed.
Moreover, we reproduced the 7Li + 118,120Sn ADs using one adjustable parameter, NICF, fixing the NRCF at the aforementioned average extracted normalizations (0.50 for 118Sn) and (0.40 for 120Sn). These results, presented as dashed curves in Figs. 8 and 9, agree well with the AD data. The optimal extracted NICF values from both (varied NRCF + varied NICF) and (fixed NRCF + varied NICF) approaches are listed in Table 3. The extracted JW values show a non-vanishing nature below the barrier, a signature of the BTA phenomenon.
-
Our systematic analysis using various potential models (DF-CDM3Y6, DF-CDM3Y6-RT, SPP, and CFP) consistently demonstrates the need to reduce the real potential strength by approximately 65%, 63%, 46%, and 50% for the 7Li + 118Sn system, and by 60%, 58%, 41%, and 60% for 7Li + 120Sn, respectively. This systematic reduction requirement originates from the significant breakup effects of 7Li in the nuclear field of the Sn targets, effects which are explicitly and accurately accounted for within the CDCC framework implemented through FRESCO calculations.
The core concept of the CDCC method is to truncate and discretize the continuum above the 7Li breakup threshold into a series of momentum bins, each treated as an excited state. This methodology allows the coupling effects of these discretized continuum states to be incorporated into the reaction calculations. This approach generates a repulsive real dynamical polarization potential (DPP) [42, 43] through continuum couplings, which explains the observed strength reduction. The extent of the model space, defined by the maximum momentum (kmax), was adjusted based on the bombarding energy. For bombarding energies between 18.15 and 20 MeV, The momentum space (k) above 7Li breakup threshold was truncated at kmax = 1.25 fm−1 (corresponding to Emax = 19.05 MeV). For energies greater than 20 MeV and up to 30 MeV, kmax was set to 1.5 fm−1 (Emax = 27.44 MeV). For the two highest energies studied, the model space was extended to kmax = 2 fm−1 (Emax = 37.34 MeV).
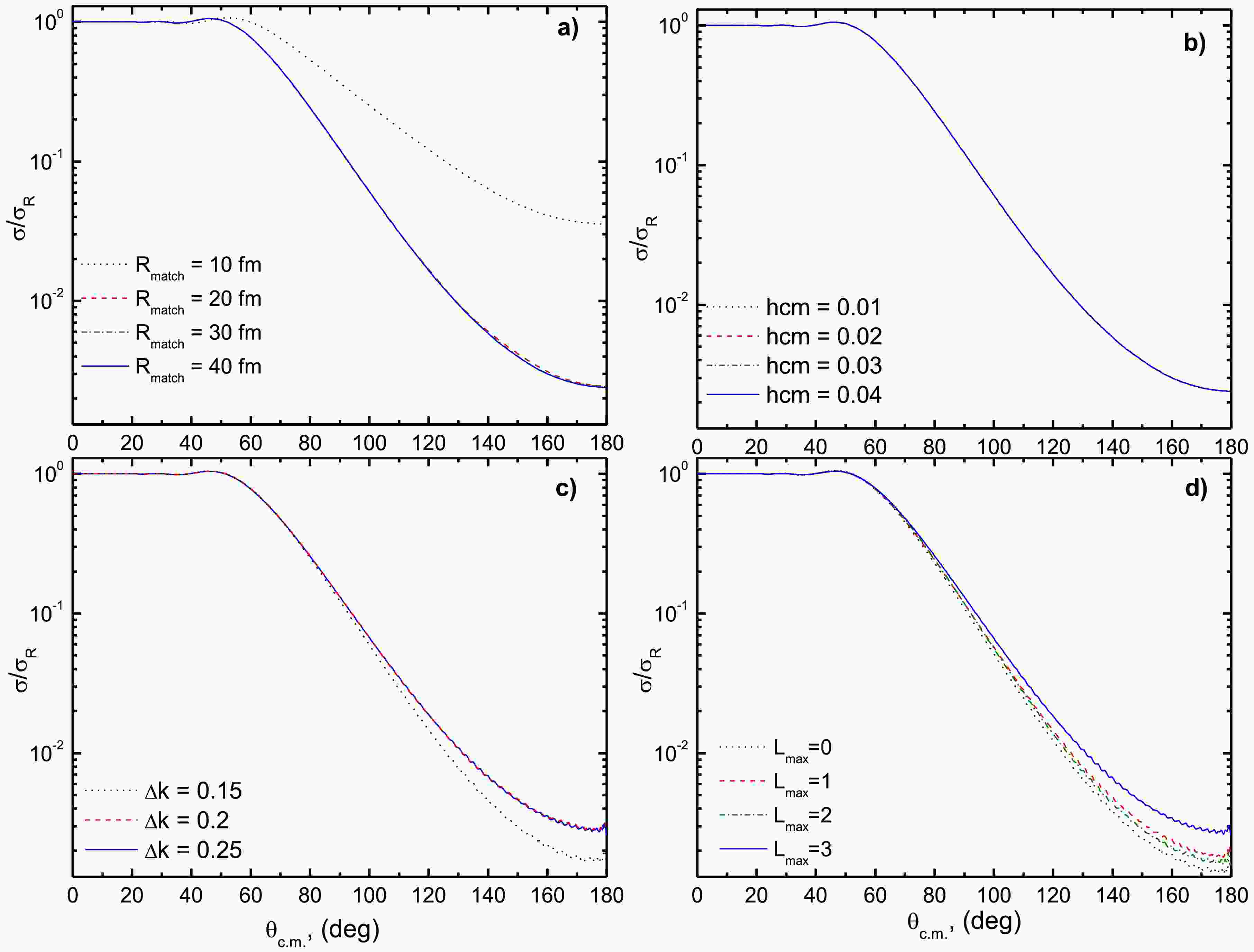
A critical aspect of CDCC calculations is ensuring their convergence, meaning the results must be independent of the choice of numerical parameters (e.g., matching radius, Rmatch, and integration step-size, hcm) or model space parameters (e.g., momentum-bin width, Δk, maximum momentum, kmax, and the inclusion of pseudo-states with different angular momenta, L). A series of test calculations were performed for the case of 7Li+120Sn at 28 MeV. These tests confirmed that the calculations are converged with the numerical parameters (Rmatch = 40 fm, hcm = 0.04 fm), as shown in Fig. 10 (a) and Fig. 10 (b). The convergence with respect to the model space was also examined. As shown in Fig. 10 (c), the calculations are converged with a bin width of Δk = 0.25 fm-1, indeed, the results for Δk = 0.2, and 0.25 fm-1 are very similar, a finding consistent with the previous study of Sakuragi et al. [42]. Furthermore, convergence test against the maximum momentum value confirmed that calculations are converged with kmax = 0.75 fm−1, as the momentum bins above this value do not contribute significantly. Finally, the model was tested with respect to the included partial waves. As shown in Fig. 10 (d), which includes pseudo-states with L= 0, 1, 2, 3, 4, the calculations show convergence at L =3.

Figure 10. (color online) Convergence tests of the CDCC calculations for 7Li + 120Sn at 28 MeV with respect to a) Rmatch, b) hcm, c) Δk, and d) Lmax.
Guided by these convergence tests, the final CDCC treatment incorporated continuum states via momentum bin discretization (0.0 ≤ k ≤0.75 fm-1 with Δk = 0.25 fm-1) [44] above the 2.468 MeV breakup threshold. This includes the significant resonant states (7/2-, Ex= 4.652 MeV and 5/2-, Ex = 6.604 MeV) with L=3 and the bound non-resonant state (1/2-, Ex= 0.4776 MeV) in addition to the 7Li ground state (3/2-, Ex= 0.0 MeV). For the coupling and diagonal potentials, we employed the cluster folding procedure outlined in Eqs. (6 and 7), using the same t + 118Sn (120Sn) and α + 118Sn (120Sn) potentials as in our CFM calculations. The CDCC method requires first calculating the projectile’s wave functions. The 7Li ground state and the 1/2- bound state were modeled as a 2P3/2 configuration using a WS potential with a radius of
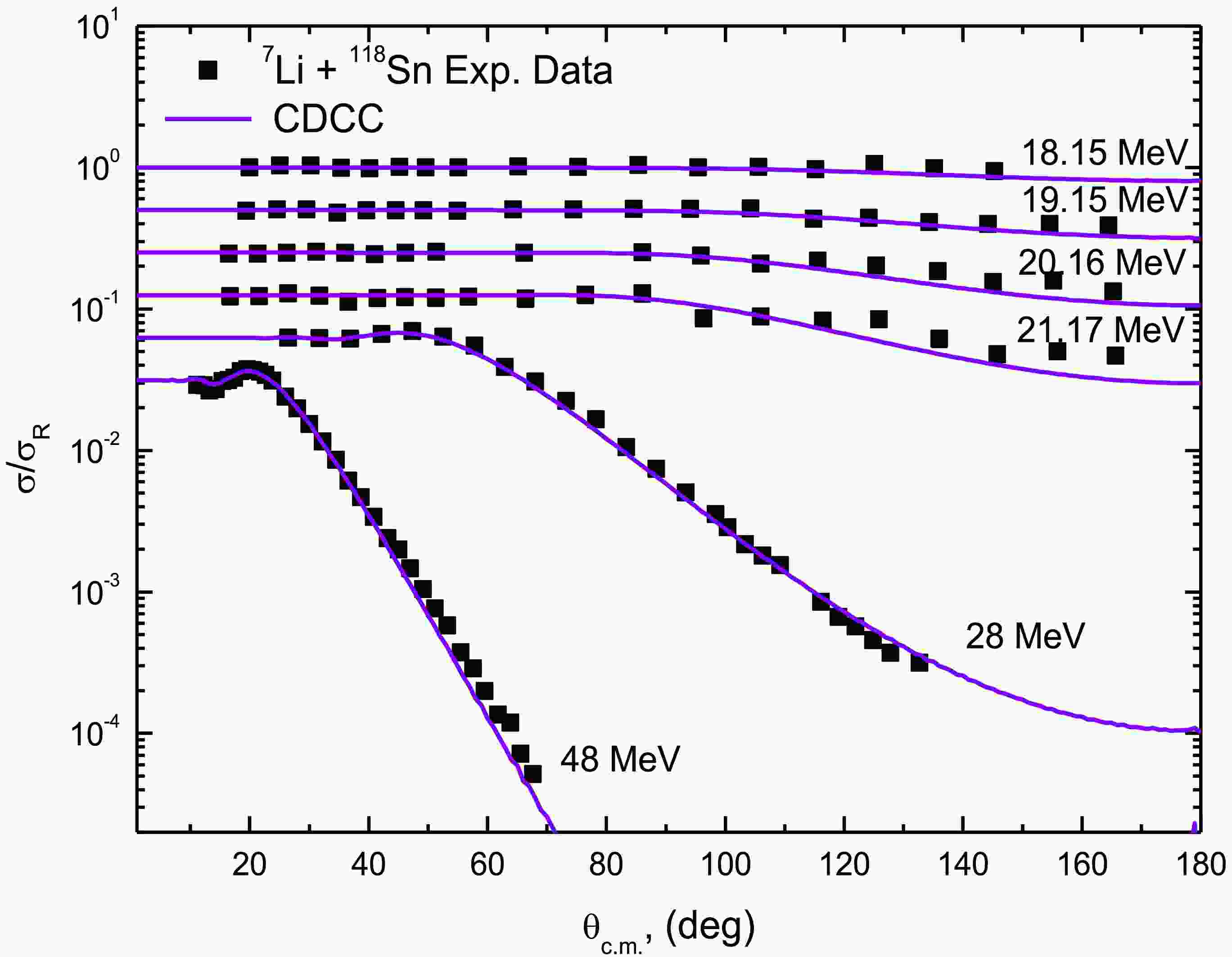
$ {\text{0}}{\text{.677 x }}\left( {{{\text{4}}^{{\text{1/3}}}} + {3^{1/3}}} \right) $ fm, a diffuseness of 0.65 fm, and a depth tuned to achieve the cluster binding energy (V0 = 96.25 MeV). The two resonant states (7/2- and 5/2-) were modeled as a 1D7/2 and 1D5/2 configurations using a WS potential with the same geometry and depths of 96.8894 and 88.8348 MeV, respectively. This two-body cluster approach for 7Li is further supported by similar findings for the 6Li nucleus. Despite 6Li having a dominant d+α cluster structure, a full four-body (n+p+α) CDCC analysis of 6Li + 209Bi scattering revealed that the dominant breakup effect is still well-captured by the simpler d+α two-body breakup channels [45]. Given the dominant role of L=3 resonances [36, 44, 46, 47], our CDCC model includes one non-resonant (1/2-) and two resonant states (7/2- and 5/2-), with widths of 0.2 and 2.0 MeV, respectively.As Figs. 11 and 12 demonstrate, the CDCC calculations achieve good agreement with experimental ADs without requiring potential normalization. The remaining minor deviations likely reflect limitations in the model space truncation and discretization or small uncertainties in the input cluster potentials. A slight oscillation observed in the calculations at backward angles for the 120Sn system (Fig. 12) is a genuine result arising from the specific interference pattern between the elastic and breakup channels at these large angles. Importantly, the success of these parameter-free calculations validates our earlier findings from simpler models, confirming that the substantial potential reductions indeed originate from dynamic polarization effects due to continuum coupling. The CDCC results provide particularly clear evidence that the DPP generated by breakup channel coupling accounts for the reduced effective potential strength needed in the other approaches. This physical interpretation unifies our understanding across all theoretical methods employed in this comprehensive study of 7Li scattering.
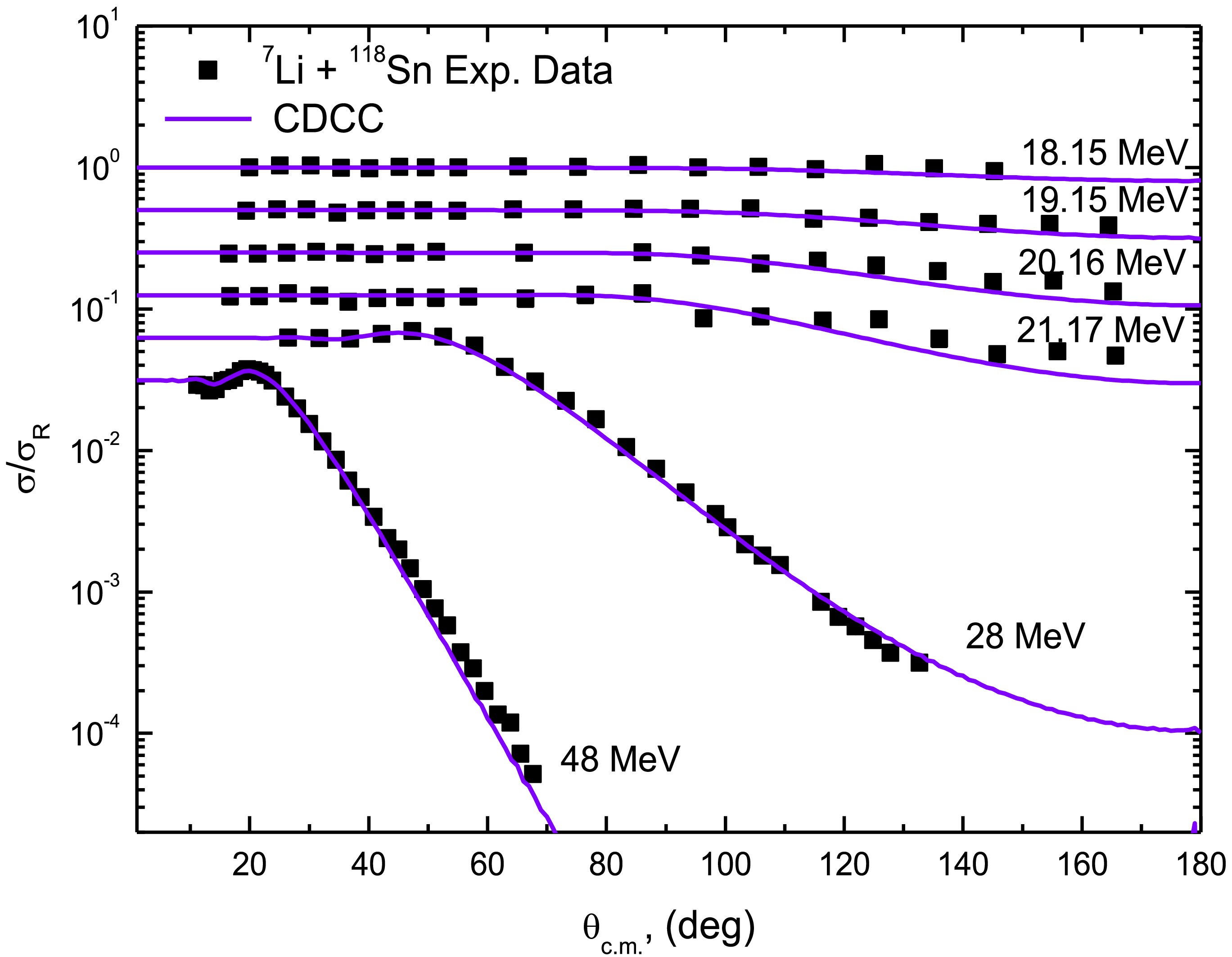
Figure 11. Experimental 118Sn(7Li,7Li)118Sn ADs (circles) versus CDCC calculations (curves) Elab= 18.15, 19.15, 20.16, 21.17, 28 and 48 MeV.
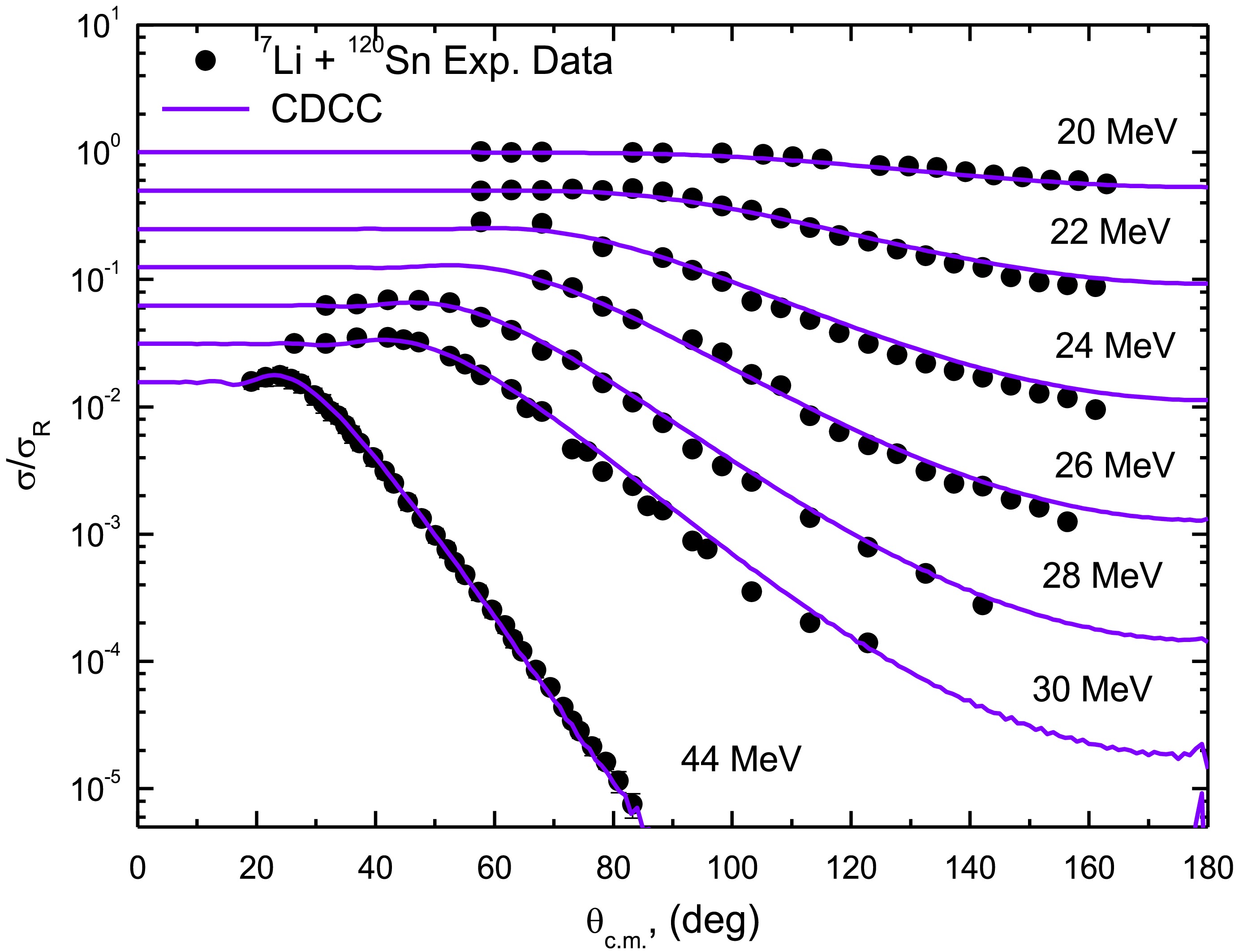
Figure 12. Experimental 120Sn(7Li,7Li)120Sn ADs (circles) versus CDCC calculations (curves) at Elab= 20, 22, 24, 26, 28, 30 and 44 MeV.
Figure 13 displays the energy-dependent reaction cross sections for the 7Li + 118,120Sn systems, calculated using multiple theoretical approaches (SPP, CDM3Y6, CDM3Y6-RT, CFM, and CDCC). The calculated cross sections exhibit systematic energy dependence that can be parameterized by the following second-order polynomial fits:
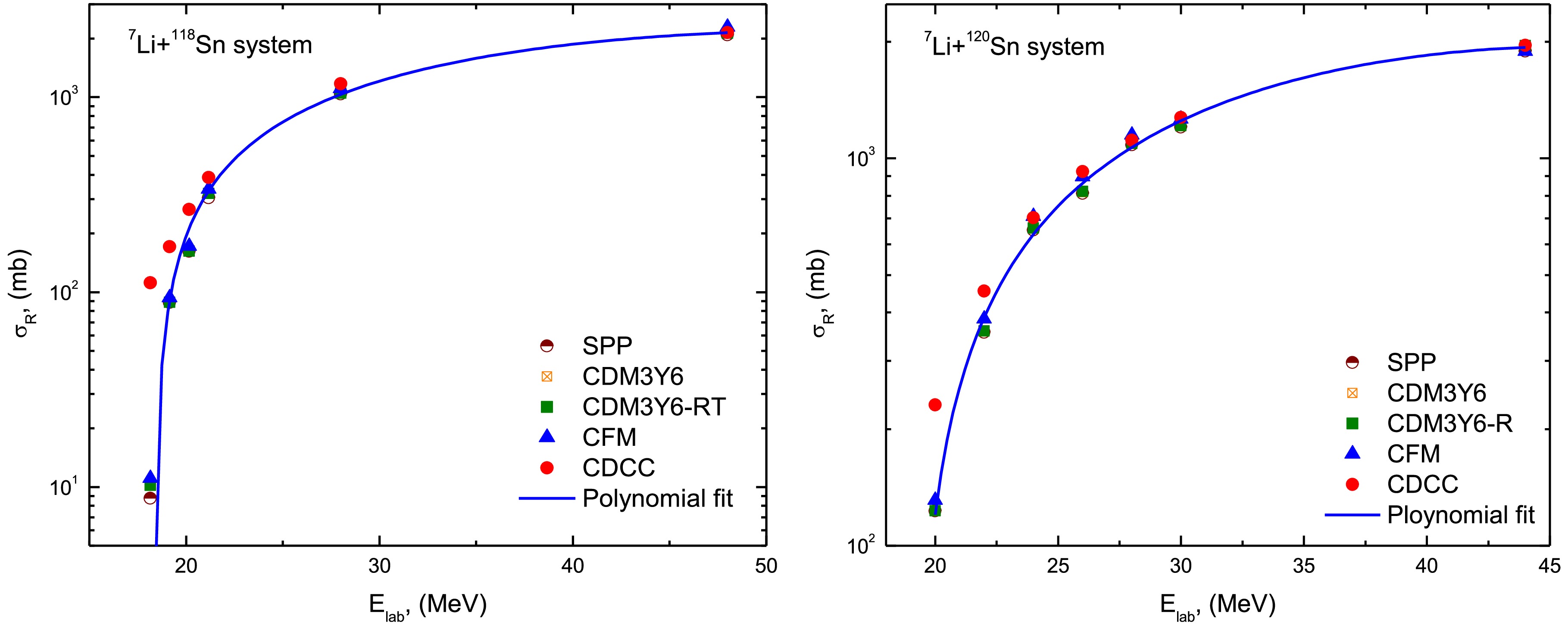
Figure 13. (color online) Energy versus the extracted σR values for 7Li + 118,120Sn systems using the different employed approaches: SPP, CDM3Y6, CDM3Y6-RT, CFM, and CDCC.
$ {\sigma _R}(E) = - 2905.6 + 190.5{\text{ }}E - 1.78{\text{ }}{E^2} $

(11) $ {\sigma _R}(E) = - 3747.5 + 246.9{\text{ }}E - 2.76{\text{ }}{E^2} $

(12) The quadratic energy dependence revealed by these polynomial fits reflects characteristic nuclear reaction dynamics observed in heavy-ion systems. For both Sn isotopes, the reaction cross sections initially increase with energy due to greater penetration of the Coulomb barrier, then gradually saturate at higher energies as nuclear interaction probabilities decrease. The systematically larger coefficients observed for the 120Sn system compared to 118Sn quantitatively capture the expected enhancement in nuclear absorption for the heavier isotope, consistent with established mass-dependent trends in heavy-ion reactions. The negative quadratic terms in both expressions physically represent the transition between competing mechanisms: at lower energies, cross sections are dominated by barrier penetration effects, while at higher energies, the reduced interaction time and increased importance of direct reaction channels become predominant.
This energy dependence pattern appears consistently across all theoretical approaches shown in Fig. 13, though with model-dependent variations that particularly highlight the significance of properly accounting for breakup effects when dealing with WB projectiles like 7Li. The polynomial parameterizations provide a useful quantitative framework for comparing the energy evolution of reaction probabilities across different theoretical treatments. Although, the extracted σR values from the various employed approaches are generally in close agreement, those obtained from the CDCC results showe a significant enhancement at the lowest studied energies.
-
Our systematic analysis using various potential models (DF-CDM3Y6, DF-CDM3Y6-RT, SPP, and CFP) consistently demonstrates the need to reduce the real potential strength by approximately 65%, 63%, 46%, and 50% for the 7Li + 118Sn system, and by 60%, 58%, 41%, and 60% for 7Li + 120Sn. This systematic reduction requirement originates from the significant breakup effects of 7Li in the nuclear field of the Sn targets. Such effects are explicitly and accurately accounted for within the CDCC framework implemented through FRESCO calculations.
The core concept of the CDCC method is truncating and discretizing the continuum above the 7Li breakup threshold into a series of momentum bins, each treated as an excited state. This methodology allows the coupling effects of these discretized continuum states to be incorporated into the reaction calculations. This approach generates a repulsive real dynamical polarization potential (DPP) [42, 43] through continuum couplings, which explains the observed strength reduction. The extent of the model space, defined by the maximum momentum (kmax), was adjusted based on the bombarding energy. For bombarding energies between 18.15 and 20 MeV, the momentum space (k) above the 7Li breakup threshold was truncated at kmax = 1.25 fm−1 (corresponding to Emax = 19.05 MeV). For energies greater than 20 MeV and up to 30 MeV, kmax was set to 1.5 fm−1 (Emax = 27.44 MeV). For the two highest energies studied, the model space was extended to kmax = 2 fm−1 (Emax = 37.34 MeV).
A critical aspect of CDCC calculations is ensuring their convergence, i.e., the results must be independent of the choice of numerical parameters (e.g., matching radius, Rmatch, and integration step-size, hcm) or model space parameters (e.g., momentum-bin width, Δk, maximum momentum, kmax, and the inclusion of pseudo-states with different angular momenta, L). A series of test calculations were performed for the case of 7Li+120Sn at 28 MeV. These tests confirmed that the calculations converged with the numerical parameters (Rmatch = 40 fm, hcm = 0.04 fm), as shown in Fig. 10 (a) and Fig. 10 (b). The convergence with respect to the model space was also examined. As shown in Fig. 10 (c), the calculations converged with a bin width of Δk = 0.25 fm-1. The results for Δk = 0.2 and 0.25 fm-1 are very similar, which is consistent with the previous study of Sakuragi et al. [42]. Furthermore, the convergence test against the maximum momentum value confirms that the calculations converge with kmax = 0.75 fm−1, as the momentum bins above this value do not contribute significantly. Finally, the model was tested with respect to the included partial waves. Figure 10 (d) shows the pseudo-states with L= 0, 1, 2, 3, 4. The calculations show convergence at L =3.

Figure 10. (color online) Convergence tests of the CDCC calculations for 7Li + 120Sn at 28 MeV with respect to a) Rmatch, b) hcm, c) Δk, and d) Lmax.
Guided by these convergence tests, the final CDCC treatment incorporated continuum states by momentum bin discretization (0.0 ≤ k ≤0.75 fm-1 with Δk = 0.25 fm-1) [44] above the 2.468 MeV breakup threshold. This included the significant resonant states (7/2-, Ex= 4.652 MeV and 5/2-, Ex = 6.604 MeV) with L=3 and the bound non-resonant state (1/2-, Ex= 0.4776 MeV) in addition to the 7Li ground state (3/2-, Ex= 0.0 MeV). For the coupling and diagonal potentials, we employed the cluster folding procedure outlined in Eqs. (6) and (7) using the same t + 118Sn (120Sn) and α + 118Sn (120Sn) potentials as in our CFM calculations. For the CDCC method, the projectile’s wave functions must be calculated first. The 7Li ground state and the 1/2- bound state were modeled as a 2P3/2 configuration using a WS potential with a radius of
$ 0.667 \times \left( {{{\text{4}}^{{\text{1/3}}}} + {3^{1/3}}} \right) $ fm, diffuseness of 0.65 fm, and depth tuned to achieve the cluster binding energy (V0 = 96.25 MeV). The two resonant states (7/2- and 5/2-) were modeled as 1D7/2 and 1D5/2 configurations using a WS potential with the same geometry and depths of 96.8894 and 88.8348 MeV, respectively. This two-body cluster approach for 7Li is further supported by similar findings for the 6Li nucleus. Despite 6Li having a dominant d+α cluster structure, a full four-body (n+p+α) CDCC analysis of 6Li + 209Bi scattering revealed that the dominant breakup effect was still well-captured by the simpler d+α two-body breakup channels [45]. Considering the dominant role of L=3 resonances [36, 44, 46, 47], our CDCC model included one non-resonant (1/2-) and two resonant states (7/2- and 5/2-), with widths of 0.2 and 2.0 MeV, respectively.As shown in Figs. 11 and 12, the CDCC calculations achieve good agreement with experimental ADs without requiring potential normalization. The remaining minor deviations likely reflect limitations in the model space truncation and discretization or small uncertainties in the input cluster potentials. A slight oscillation observed in the calculations at backward angles for the 120Sn system (Fig. 12) is a genuine result arising from the specific interference pattern between the elastic and breakup channels at these large angles. Importantly, the success of these parameter-free calculations validates our earlier findings from simpler models, confirming that the substantial potential reductions indeed originate from dynamic polarization effects due to continuum coupling. The CDCC results provide particularly clear evidence that the DPP generated by breakup channel coupling accounts for the reduced effective potential strength needed in the other approaches. This physical interpretation unifies our understanding across all theoretical methods employed in this comprehensive study of 7Li scattering.

Figure 11. (color online) Experimental 118Sn(7Li,7Li)118Sn ADs (circles) versus CDCC calculations (curves) Elab= 18.15, 19.15, 20.16, 21.17, 28 and 48 MeV.

Figure 12. (color online) Experimental 120Sn(7Li,7Li)120Sn ADs (circles) versus CDCC calculations (curves) at Elab= 20, 22, 24, 26, 28, 30, and 44 MeV.
Figure 13 displays the energy-dependent reaction cross sections for the 7Li + 118,120Sn systems, calculated using multiple theoretical approaches (SPP, CDM3Y6, CDM3Y6-RT, CFM, and CDCC). The calculated cross sections exhibit systematic energy dependence that can be parameterized by the following second-order polynomial fits:

Figure 13. (color online) Energy versus the extracted σR values for 7Li + 118,120Sn systems using the different employed approaches: SPP, CDM3Y6, CDM3Y6-RT, CFM, and CDCC.
$ {\sigma _R}(E) = - 2905.6 + 190.5{\text{ }}E - 1.78{\text{ }}{E^2}, $

(11) $ {\sigma _R}(E) = - 3747.5 + 246.9{\text{ }}E - 2.76{\text{ }}{E^2}. $

(12) The quadratic energy dependence revealed by these polynomial fits reflects characteristic nuclear reaction dynamics observed in heavy-ion systems. For both Sn isotopes, the reaction cross sections initially increase with energy owing to greater penetration of the Coulomb barrier, then gradually saturate at higher energies as nuclear interaction probabilities decrease. The systematically larger coefficients observed for the 120Sn system compared to 118Sn quantitatively capture the expected enhancement in nuclear absorption for the heavier isotope, consistent with established mass-dependent trends in heavy-ion reactions. The negative quadratic terms in both expressions physically represent the transition between competing mechanisms. At lower energies, cross sections are dominated by barrier penetration effects, while at higher energies, the reduced interaction time and increased importance of direct reaction channels become predominant.
This energy dependence pattern appears consistently across all theoretical approaches shown in Fig. 13, nevertheless the model-dependent variations particularly highlight the significance of properly accounting for breakup effects when dealing with WB projectiles such as 7Li. The polynomial parameterizations provide a useful quantitative framework for comparing the energy evolution of reaction probabilities across different theoretical treatments. Although the extracted σR values from the various employed approaches are generally in close agreement, those obtained from the CDCC results show a significant enhancement at the lowest studied energies.
-
This systematic study of 7Li elastic scattering from 118,120Sn nuclei across an energy range of 18–48 MeV reveals the dominance of the projectile's weak binding and cluster structure in governing the reaction dynamics. All employed theoretical approaches from folding models to microscopic CDCC calculations consistently demonstrate that accurate descriptions require 40−65% reductions in the real potential strength. This substantial renormalization directly reflects the dynamic polarization potential arising from coupling to breakup channels.
While simpler models achieve good fits through empirical normalization factors, the CDCC framework successfully reproduces the data without adjustments by explicitly treating continuum states, confirming these reductions as physical effects rather than artifacts. The cluster folding model's success further underscores the importance of properly accounting for the α+t structure of7Li .
The reaction cross sections exhibit characteristic energy dependence, initially rising owing to barrier penetration and saturating at higher energies. Polynomial fits capture these trends, while revealing subtle mass-dependent differences between targets. Notably, the conventional threshold anomaly is absent, replaced by smooth energy dependence consistent with persistent breakup effects across the studied range.
Collectively, these results establish that reliable descriptions of WB nuclear systems must incorporate both cluster degrees of freedom and continuum coupling. This provides a unified understanding that bridges phenomenological and microscopic approaches, offering valuable benchmarks for future theoretical developments. The CDCC method emerges as a particularly robust approach for such systems, though appropriately normalized folding potentials offer a practical and effective alternative when full coupled-channel calculations are impractical.
-
This systematic study of 7Li elastic scattering from 118,120Sn nuclei across an energy range of 18–48 MeV reveals the dominance of the projectile's weak binding and cluster structure in governing the reaction dynamics. All theoretical approaches employed—from folding models to microscopic CDCC calculations—consistently demonstrate that accurate descriptions require 40-65% reductions in the real potential strength. This substantial renormalization directly reflects the dynamic polarization potential arising from coupling to breakup channels.
While simpler models achieve good fits through empirical normalization factors, the CDCC framework successfully reproduces the data without adjustments by explicitly treating continuum states, confirming these reductions as physical effects rather than artifacts. The cluster folding model's success further underscores the importance of properly accounting for 7Li's α+t structure.
Reaction cross sections exhibit characteristic energy dependence, initially rising due to barrier penetration and saturating at higher energies. Polynomial fits capture these trends while revealing subtle mass-dependent differences between targets. Notably, the conventional threshold anomaly is absent, replaced by smooth energy dependence consistent with persistent breakup effects across the studied range.
Collectively, these results establish that reliable descriptions of WB nuclear systems must incorporate both cluster degrees of freedom and continuum coupling. This provides a unified understanding that bridges phenomenological and microscopic approaches, offering valuable benchmarks for future theoretical developments. The CDCC method emerges as particularly robust approach for such systems, though appropriately normalized folding potentials offer practical and effective alternative when full coupled-channels calculations are impractical.
Breakup of 7Li in the field of 118,120Sn nuclei and its effect on the elastic scattering channel
- Received Date: 2025-08-10
- Available Online: 2026-02-15
Abstract: The breakup of weakly-bound projectiles has been shown to significantly influence scattering processes, including elastic scattering. In this context, we revisit the angular distributions (ADs) for the elastic scattering of 7Li from 118Sn and 120Sn targets. The study analyzes 7Li + 118Sn ADs over the energy range of 18.15–48 MeV and 7Li + 120Sn ADs from 20 to 44 MeV, utilizing various nuclear interaction models, including the São Paulo potential, CDM3Y6 potential (with and without the rearrangement term), and cluster folding model. The results indicate that the real component of the folded potentials must be scaled down by 40–65% to achieve an accurate fit to the experimental ADs, underscoring the prominent role of 7Li breakup effects. Interestingly, the conventional threshold anomaly observed in reactions involving tightly bound nuclei is not present. Further analysis using the continuum discretized coupled channels (CDCC) approach provides excellent agreement with the data, reinforcing these findings.





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF













 DownLoad:
DownLoad: