-
It is well known that a curvature singularity could be formed during a gravitational collapse. There might exist three types of these singularities, namely space-like, light-like and time-like. Among them, the undetermined initial data on a time-like singularity would cause the breakdown of determinism of general relativity. Although there exist some solutions to Einstein's equation admitting time-like singularities (e.g. Kerr-Newman and Reissner-Nordstrom black hole solutions), claiming that general relativity could lose predictability is rather subtle due to the presence of the Cauchy horizon, which encloses the time-like singularity. In particular, to rescue the predictability of general relativity, Penrose proposed the strong cosmic censorship (SCC) conjecture, which asserts that the maximal Cauchy development of physically acceptable initial conditions is locally inextendible as a regular manifold [1-3]. Consequently, when the initial data is perturbed outside of a black hole, whether SCC holds true crucially depends on the extensibility of the perturbation (e.g., the metric and other fields) at the Cauchy horizon.
To give a more rigorous definition of the extensibility of the perturbation across the Cauchy horizon, several formulations of SCC have been proposed. For example, the
$ C^{r} $ version of SCC states that the metric cannot be$ C^{r}(r\in N) $ smooth at the Cauchy horizon [4, 5]. Various pieces of evidence suggest that the Cauchy horizon can be extendible with a continuous metric for the perturbed initial data, indicating the falsity of the$ C^{0} $ version of SCC [6-8]. On the other hand, it has been argued that the$ C^{2} $ version of SCC appears to be true since the curvature blows up at the Cauchy horizon [9]. However, an observer can still experience a finite tidal force and cross the Cauchy horizon even when the metric is inextendible in$ C^{2} $ [10]. So requiring that the metric is$ C^{2} $ at the Cauchy horizon seems to be too strong, and extensions with lower smoothness shall be considered.It is worth noting that weak solutions can have many important physical applications, in which
$ C^{r} $ smooth solutions are not available. Therefore it might be a more appropriate choice to characterize the extensibility of the Cauchy horizon by considering whether the perturbation is inextendible as a weak solution. For Einstein's equation, a weak solution is specified by locally square integrable Christoffel symbols in some charts of the manifold. This observation then leads to the Christodoulou formulation of SCC, which states that the maximal Cauchy development should be inextendible as a spacetime with locally square integrable Christoffel symbols [11]. Practically, for a linear scalar perturbation, the Christodoulou version of SCC can be tested by checking whether the scalar field will belong to the Sobolev space$ H_{loc}^{1} $ at the Cauchy horizon. Note that if the perturbation belongs to the Sobolev space$ H_{loc}^{1} $ , its first derivative is locally square integrable. In other words, if SCC is violated in the Christodoulou version, the perturbation belongs to$ H_{loc}^{1} $ and, roughly speaking, has finite energy at the Cauchy horizon.To check the validity of the SCC, one needs to analyze the evolution of the perturbation, which is governed by two mechanisms. One is the mass-inflation mechanism, associated with the exponential amplification of a perturbation due to the blue-shift effect, which might cause a singular behavior at the Cauchy horizon [7, 9, 10, 12-14]. The other is the time-dependent remnant perturbation decaying outside of the black hole, which can compete with the mass inflation to invalidate SCC. For an asymptotically flat black hole with the perturbation outside the black hole decaying in an inverse power-law way, the mass-inflation mechanism dominates to render the Cauchy horizon unstable [7, 15-18]. Interestingly, the exponential decay of the perturbation is observed in asymptotically dS spacetime, indicating that mass inflation might not be strong enough to keep SCC valid. Quantitatively, for a linear scalar perturbation in an asymptotic dS black hole, the competition between the the mass inflation and remnant decaying is characterized by [19-24]
$ \beta\equiv\frac{\alpha}{\kappa_{-}}, $

(1) where
$ \kappa_{-} $ denotes the surface gravity at the Cauchy horizon, and$ \alpha $ is the spectral gap representing the distance from the real axis to the lowest-lying quasi-normal mode (QNM) on the lower half of the complex plane of frequency. It shows that$ \beta>1/2 $ corresponds to the violation of the Christodoulou version of SCC. Moreover,$ \beta>1 $ represents the$ C^{1} $ extensibility of a scalar field at the Cauchy horizon, leading to the bounded curvature if coupled to gravity [19, 23, 25]. Hence$ \beta>1 $ implies the violation of SCC in the$ C^{2} $ version, opening the possibility to the existence of solutions with even higher regularity across the Cauchy horizon. From now on, the term “SCC” only refers to the Christodoulou version of SCC.Recently, the validity of SCC has been widely explored in asymptotic dS black holes. In particular, the authors of Refs. [23, 26-31] considered scalar perturbations with/without mass and charge in a Reissner-Nordstrom-de Sitter (RNdS) black hole, and found that SCC is violated in the near-extremal region. The analysis has been extended to the Dirac field perturbation [32-35] and higher space-time dimensions [36-38], where there still exists some room for the violation of SCC. Especially in Refs. [26, 33], it has been observed that the
$ C^{2} $ version of SCC can be violated, since$ \beta>1 $ appears in some near-extremal parameter regimes. Even worse, if one considers the case with the coupled linearized electromagnetic and gravitational perturbations in a RNdS black hole, the$ C^{r} $ version of SCC for any$ r\geqslant 2 $ can be violated by taking the black hole close enough to extremality [25]. Moreover, the authors of Refs. [34, 39, 40] argued that nonlinear effects could not save SCC from being violated for a near-extremal RNdS black hole. Surprisingly, SCC can always be respected for the massless scalar field and linearized gravitational perturbations in a Kerr-dS black hole [36, 41].It is interesting and inspiring to check the validity of SCC in models beyond the Einstein-Maxwell theory. In Refs. [42, 43], we studied SCC for dS black holes in the Einstein-Born-Infeld and Einstein-Logarithmic systems and found that the nonlinear electrodynamics effects tend to rescue SCC. In addition, SCC has been tested for a scalar field perturbation in the Horndeski theory in Ref. [44], which showed that the higher-order derivative couplings increase the regularity requirements for the existence of weak solutions beyond the Cauchy horizon. On the other hand, Gauss-Bonnet (GB) gravity, which arises from the low-energy effective action of heterotic string theory [45], has attracted considerable attention in the literature. Coupling to Maxwell electrodynamics, namely in the Einstein-Maxwell-Gauss-Bonnet (EMGB) theory, the EMGB black hole solution has been obtained, and various aspects have been extensively investigated [46-56]. To the best of our knowledge, little is known about the validity of SCC in the EMGB theory. The purpose of this paper is to investigate the validity of SCC for a neutral massless scalar perturbation propagating in
$ 5 $ - and$ 6 $ -dimensional EMGBdS black holes.The rest of the paper is organized as follows. In Sec. II, we briefly review the
$ 5 $ - and$ 6 $ -dimensional EMGBdS black hole solutions and obtain the allowed parameter regions, where the Cauchy horizon exists. In Sec. III, we show how to compute the QNMs for a neutral massless scalar perturbation in an EMGBdS black hole. In Sec. IV, we present and discuss the numerical results in various parameter regions. We summarize our results and conclude with a brief discussion in the last section. For simplicity, we set$ G = c = 1 $ in this paper. -
In this section, we briefly review the EMGBdS black hole solution and obtain the parameter region where three horizons exist. The action of the Einstein-Maxwell-Gauss-Bonnet theory in d-dimensional spacetime is given by [46]
$ \begin{aligned}[b]S =& \frac{1}{16\pi}\int {\rm d}^{d}x\sqrt{-g}\left[{\cal R}-2\varLambda+\alpha_{\rm GB}\left(R^{2}-4R_{\mu\nu}R^{\mu\nu}\right.\right.\\&\left.\left.+R_{\mu\nu\rho\sigma}R^{\mu\nu\rho\sigma}\right)-F^{\mu\nu}F_{\mu\nu}\right], \end{aligned}$

(2) where
$ \varLambda>0 $ is the cosmological constant,$ {\cal R} $ is the Ricci scalar curvature, and$ F_{\mu\nu} = \partial_{\mu}A_{\nu}-\partial_{\nu}A_{\mu} $ is the electromagnetic tensor field of the electromagnetic field$ A_{\mu} $ . It is noteworthy that the GB coupling constant$ \alpha_{\rm GB} $ is naturally assumed to be positive, since the GB correction to the Einstein gravity is well-motivated from the low-energy effective action of heterotic string theory [45]. So we focus on$ \alpha_{\rm GB}\geqslant 0 $ in this paper. In addition, the GB term is known to be topological with no dynamics in the$ d = 4 $ dimension. Therefore, we shall consider$ d\geqslant 5 $ in what follows.For the action (2), a static spherically symmetric black hole solution was obtained in Refs. [46, 48, 51]:
$\begin{aligned}[b] {\rm d}s^{2} =& -f\left(r\right){\rm d}t^{2}+\frac{{\rm d}r^{2}}{f\left(r\right)}+r^{2}{\rm d}\Omega_{d-2}^{2},\\{{A}} =& A_{t}{\rm d}t = -\frac{4\pi Q}{(d-3)\omega_{d-2}r^{d-3}}{\rm d}t, \end{aligned} $

(3) with the blackening factor
$ f\left(r\right) = 1+\frac{r^{2}}{2\widetilde{\alpha}}-\frac{r^{2}}{2\widetilde{\alpha}}\sqrt{1+4\widetilde{\alpha}\left[\frac{2\varLambda}{(d-2)(d-1)}+\frac{16\pi M}{\left(d-2\right)\omega_{d-2}r^{d-1}}-\frac{32\pi^{2}Q^{2}}{\left(d-2\right)\left(d-3\right)\omega_{d-2}^{2}r^{2d-4}}\right]}, $

(4) where M and Q are the ADM mass and the electric charge of the EMGBdS black hole, respectively, and
${\rm d}\Omega_{d-2}^{2}$ represents the line element of a$ (d-2) $ -dimensional unit sphere with volume$ \omega_{d-2} = 2\pi^{(d-1)/2}/\Gamma((d-1)/2) $ . For simplicity, we introduce a redefined GB parameter$ \widetilde{\alpha} = \alpha_{\rm GB}\left(d-3\right)\left(d-4\right) $ . In the limit of$ \widetilde{\alpha}\rightarrow0 $ , Eqs. (3) and (4) reduce to the d-dimensional RNdS black hole as expected [37].An EMGBdS black hole is characterized by the parameters M, Q,
$ \varLambda $ and$ \widetilde{\alpha} $ . It can be shown that an EMGBdS black hole can possess one, two or three horizons in different parameter regimes. The topology and causal structure of EMGBdS black holes have been analyzed in detail in Ref. [50]. To study SCC, we need to find the “allowed” region in parameter space, in which the black hole possesses three horizons, namely the Cauchy horizon$ r_{-} $ , the event horizon$ r_{+} $ and the cosmological horizon$ r_{c} $ . For later use, we denote the surface gravity$ \kappa_{h}\equiv\left|f^{\prime}\left(r_{h}\right)\right|/2 $ with$ h\in\{+,-,c\} $ for each horizon. The allowed region is determined by the two limits, namely the extremal limit with$ r_{-} = r_{+} $ , which corresponds to the extremal black hole with charge$ Q_{ \rm{ext}} $ , and the Nariai limit with$ r_{+} = r_{c} $ , which corresponds to the Nariai black hole with charge$ Q_{ \rm{nar}} $ . Hence, the allowed region is given by$ Q_{ \rm{nar}}<Q<Q_{ \rm{ext}} $ or$ 0<Q<Q_{ \rm{ext}} $ if no Nariai limit exists. In particular, a$ 5 $ -dimensional EMGBdS black hole has$ Q_{ \rm{nar}} = \pi\sqrt{-2+3k-2\left(1-k\right)^{3/2}}/\varLambda $

and
$ Q_{\text{ext}} = \pi\sqrt{-2+3k+2\left(1-k\right)^{3/2}}/\varLambda $

with
$ k\equiv\varLambda(8M-3\pi\widetilde{\alpha})/(6\pi) $ [57]. The existence of$ Q_{ \rm{nar}} $ and$ Q_{\text{ext}} $ requires$ \widetilde{\alpha}<8M/(3\pi), $ which puts an upper bound on$ \alpha. $ If$ \varLambda>\varLambda_{\rm{c}}\equiv3\pi/\left(4M\right) $ ,$ Q_{ \rm{nar}} $ could only exist when$ \widetilde{\alpha}>8M/(3\pi)-2/\varLambda $ , which puts a nonzero lower bound on$ \alpha $ . However for$ d\geqslant 6 $ , the allowed region can only be determined numerically. For example, our numerical results show that, for$ d = 6 $ , there is no upper bound on$ \widetilde{\alpha} $ , and a nonzero lower bound on$ \widetilde{\alpha} $ appears when$ \varLambda>\varLambda_{\rm{c}}\sim6.348M^{-2/3} $ .The allowed regions and their boundaries in the
$ \widetilde{\alpha} $ -Q parameter space are plotted in Fig. 1 for various values of$ \varLambda $ in the$ d = 5 $ and$ d = 6 $ cases. Without loss of generality, we set$ M = 1 $ in the rest of this paper. When$ \varLambda>\varLambda_{\rm{c}} $ , the right-hand column of Fig. 1 shows that the allowed regions have a nonzero minimum value of$ \widetilde{\alpha} $ , marked by the point$ A, $ as expected. One can also notice that, for the allowed region,$ \widetilde{\alpha}<8/\left(3\pi\right) $ in the$ d = 5 $ case, while no upper bound on$ \widetilde{\alpha} $ exists in the$ d = 6 $ case. Furthermore, we find that the allowed regions are very similar in the$ d\geq6 $ cases. We show the allowed regions for the$ d = 7 $ and$ d = 8 $ cases in Fig. 2, showing remarkable similarities to the$ d = 6 $ case. Thus we shall consider only two cases, those for$ d = 5 $ and$ d = 6 $ , in what follows.
Figure 1. (color online) The regions in light blue are allowed to possess three horizons for EMGBdS black holes with
$ d = 5 $ (upper row) and$ d = 6 $ (lower row) for various values of$ \varLambda $ . The dashed orange and green lines represent the extremal black hole and the Nariai black hole, respectively. When$ \varLambda>\varLambda_{\rm{c}} $ (right column), there exists a tipping point A, which marks a nonzero minimum value of$ \widetilde{\alpha} $ . The solid red line, which represents the near-extremal black hole with the charge ratio$ Q/Q_{ \rm{ext}} = 0.9 $ , intersects the dashed green line at point B, where SCC tends to be saved, as discussed below.
Figure 2. (color online) The regions in light blue are allowed to possess three horizons for EMGBdS black holes with
$ d = 7 $ (upper row) and$ d = 8 $ (lower row) for various values of$ \varLambda $ . The dashed orange and green lines represent the extremal black hole and the Nariai black hole, respectively. The allowed regions in the$ d = 6 $ , 7 and 8 cases are quite alike. -
In this section, we discuss QNMs for a neutral massless scalar perturbation in d-dimensional EMGBdS spacetime. The behavior of the neutral massless scalar field is governed by the Klein-Gordon equation
$ {\nabla}^{2}\Phi = 0, $

(5) where
$ {\nabla} $ is the covariant derivative. To facilitate our numerical calculation, we use the Eddington-Finkelstein ingoing coordinates$ \left(v,r,{\bf{\Omega}}_{d-2}\right) $ with$ v = t+r_{*} $ , where$ r_{*} $ is the tortoise coordinate defined as${\rm d}r_{*} = {\rm d}r/f(r)$ . In addition, we choose an appropriate gauge transformation such that${{A}} = A_{v}{\rm d}v = -4\pi Q{\rm d}v/((d-3)\omega_{d-2}r^{d-3})$ . Since the EMGBdS black hole solution is static and spherically symmetric, a mode solution of Eq. (5) can have the separable form$ \Phi(v,r,{\bf{\Omega}}_{d-2}) = \mathop{\sum\limits_{lm_{j}}}\psi_{\omega lm_{j}}(r)Y_{lm_{j}}({\bf{\Omega}}_{d-2}){\rm e}^{-{\rm i}\omega v}. $

(6) Here, l and
$ m_{j} $ $ (j = 1,2,\cdots,d-3) $ denote the integers required to uniquely determine a$ (d-2) $ -hyperspherical harmonic$ Y_{lm_{j}}({\bf{\Omega}}_{d-2}) $ , which fulfills$ \nabla_{\bf{S}^{d-2}}^{2}Y_{lm_{j}}({\bf{\Omega}}_{d-2}) = -l(l+d-3)Y_{lm_{j}}({\bf{\Omega}}_{d-2}) $ . Since no “magnetic splitting” is present due to the spherical symmetry of the background, the index$ m_{j} $ can be suppressed in$ \psi_{\omega lm_{j}} $ [58, 59]. Plugging Eq. (6) into Eq. (5), we obtain the radial equation$ \begin{aligned}[b] &\left(r^{2}f\partial_{r}^{2}+\left(-2i\omega r^{2}+r^{2}f'+(d-2)rf\right)\partial_{r}\right.\\&\quad \left.-i(d-2)\omega r-l(l+d-3)\right)\psi_{\omega l}(r) = 0, \end{aligned}$

(7) where
$ f^{\prime} $ denotes${\rm d}f(r)/{\rm d}r$ .One can perform the Frobenius method to obtain the solutions near the event and cosmological horizons, respectively. If we impose the ingoing boundary condition at the event horizon and the outgoing boundary condition at the cosmological horizon, namely,
$ \psi_{\omega l}^{ \rm{ingoing}}(r\rightarrow r_{h})\sim {\rm{const.}},\quad\psi_{\omega l}^{ \rm{outgoing}}(r\rightarrow r_{c})\sim(r-r_{c})^{-{\rm i}\omega/\kappa_{c}}, $

(8) then Eq. (7) selects a set of discrete frequencies
$ \omega_{ln} $ $ (n = 1,2,\cdots) $ , which are QNMs of the scalar field [60]. There are many analytic and numerical ways to extract QNMs [60, 61]. In this paper, we employ the Chebyshev collocation scheme and the associated Mathematica package developed in Refs. [62-64]. The basic idea to compute the spectrum efficiently is to discretize the QNM equations by the pseudospectral method and solve the resulting generalized eigenvalue equation. It can produce an additional infinite set of purely imaginary modes, which are known to be missed by the WKB approximation [60]. Moreover, the WKB approximation assumes that the potential has a single extremum, which may fail in some cases [65].To adapt our numerical scheme for the Mathematica package, we redefine the field
$ \psi_{\omega l} $ as$ \psi_{\omega l} = \frac{1}{x}\left(1-x\right)^{-{\rm i}\omega/\kappa_{c}}\phi_{\omega l}, $

(9) with a new coordinate
$ x\equiv(r-r_{+})/(r_{c}-r_{+}) $ , which renders the new field$ \phi_{\omega l} $ regular at both the event and cosmological horizons. After the radial equation for$ \phi_{\omega l} $ is obtained from Eqs. (7) and (9), one can use the package to find a series of QNMs,$ \omega_{ln} $ . The spectral gap$ \alpha $ in Eq. (1) is then given by$ \alpha = {\rm{inf}}_{ln}\left\{ - {\rm{Im }}\omega_{ln}\right\} $ . -
In this section, we present the numerical results for QNMs for a neutral massless scalar perturbation in
$ 5 $ - and$ 6 $ -dimensional EMGBdS black holes and check the validity of SCC. These results were obtained using the Mathematica package of Refs. [62-64] and found to be consistent with the results of Refs. [37, 49, 66, 67] in various limits. Since it has been shown that SCC could be violated in a near-extremal RNdS black hole, we will focus on the near-extremal regime of the EMGBdS black holes. -
We first study the
$ d = 5 $ case. For a near-extremal black hole, it is well known that there exist three qualitatively different families of QNMs: the photon sphere (PS) family, which can be traced back to the photon sphere, the de Sitter (dS) family, which is deformation of the pure de Sitter modes, and the near-extremal (NE) family, which only appears for near-extremal black holes [23, 33, 37, 42, 68]. We plot these three distinct families for a 5-dimensional near-extremal EMGBdS black hole in Fig. 3, where we consider two cases with$ \varLambda = 1 $ and$ \varLambda = 3 $ , since their allowed regions are quite different, as depicted in Fig. 1. As shown in Fig. 3(a), when$ Q/Q_{ \rm{ext}} $ increases toward the extremal limit,$ {\rm{ Im}}(\omega)/\kappa_{-} $ for the PS and dS dominant modes become divergent while the NE mode takes over to make$ \beta $ finite but smaller than$ -1/2 $ . Therefore, like a RNdS black hole, the presence of the NE mode can invalidate SCC as long as the EMGBdS black hole lies close enough to extremality. As one increases$ \widetilde{\alpha} $ from the left column to the right column in Fig. 3(a), the SCC violation range of$ Q/Q_{ \rm{ext}} $ expands, which implies that the GB term in the action (2) tends to worsen the SCC violation for a scalar in a 5-dimensional near-extremal EMGBdS black hole. To better understand how the GB term affects the validity of SCC, we plot$ {\rm{ Im}}(\omega)/\kappa_{-} $ against$ \widetilde{\alpha} $ with increasing$ Q/Q_{ \rm{ext}} $ from the left column to the right column in Fig. 3(b). The SCC violation range of$ \widetilde{\alpha} $ , which is to the right of the thick dashed vertical lines, increases as$ Q/Q_{ \rm{ext}} $ increases, indicating that SCC tends to be violated when the black hole is closer to extremality. Note that there is an upper bound$ \widetilde{\alpha} = 8/(3\pi) $ on$ \widetilde{\alpha} $ for$ d = 5 $ , as discussed before. Moreover, as shown in Fig. 4, the$ {\rm{ Im}}(\omega)/\kappa_{-} $ of all three families' dominant modes decreases to some finite values when$ \widetilde{\alpha} $ increases toward the upper bound. Figure 3(b) shows that, for a scalar in a 5-dimensional near-extremal EMGBdS black hole, SCC is always violated when$ \widetilde{\alpha} $ is close enough to the upper bound.
Figure 3. (color online) Dominant modes of three families for a neutral massless scalar field in a
$ 5 $ -dimensional EMGBdS black hole, showing the dominant NE mode (green lines) at$ l = 0 $ , the dominant dS mode (red lines) at$ l = 1 $ and the (nearly) dominant complex PS mode (blue lines) at$ l = 10 $ . The threshold$ \beta\equiv- {\rm{ Im}}(\omega)/\kappa_{-} = 1/2 $ is designated by thick dashed vertical lines, to the right of which SCC is violated. The dashed vertical lines in the insets denote$ \beta = 1 $ .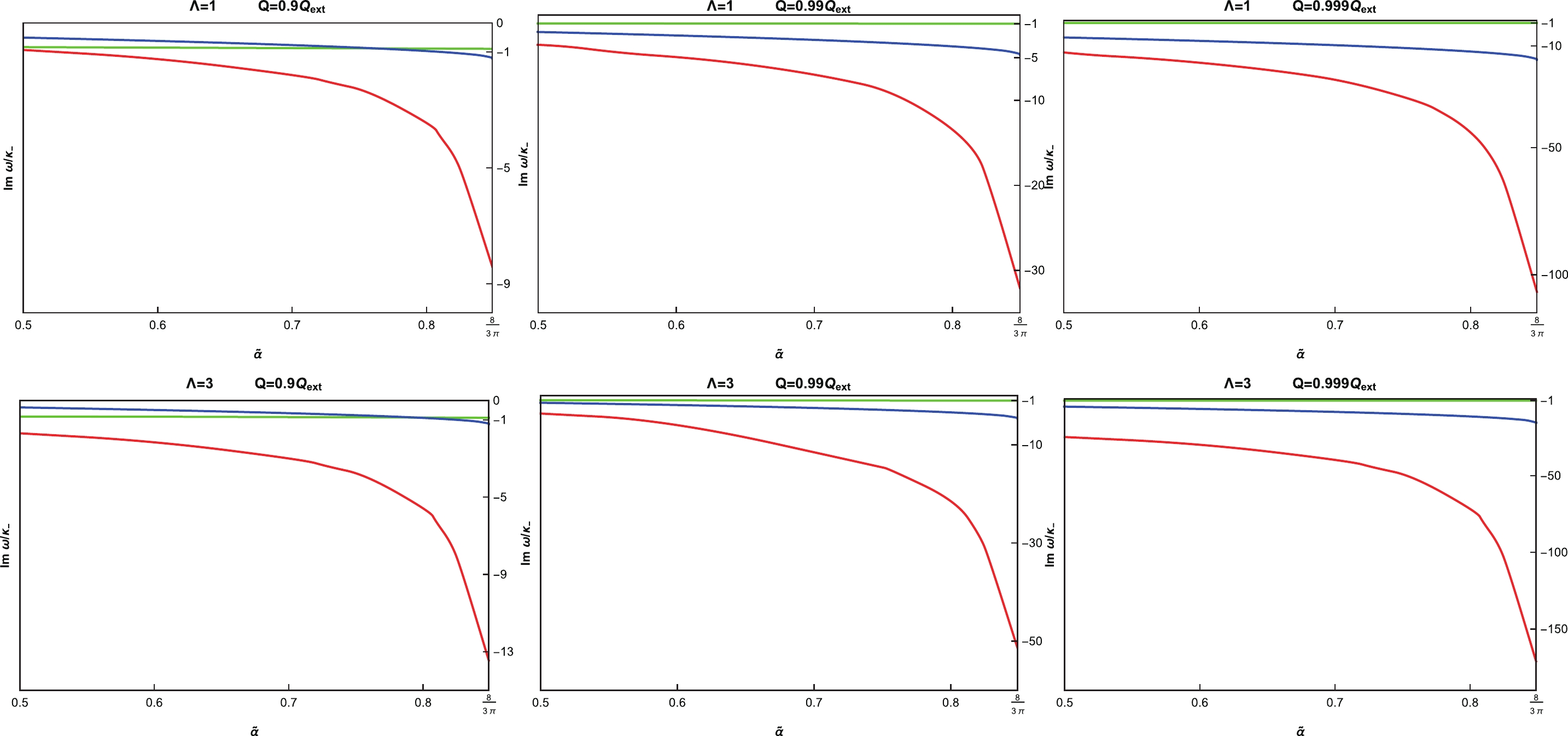
Figure 4. (color online) Dominant modes of three families near the upper bound of
$ \widetilde{\alpha} $ , for a neutral massless scalar field in a$ 5 $ -dimensional EMGBdS black hole with various$ \varLambda $ and$Q/Q_{\rm ext}$ . It shows that the$ {\rm{ Im}}(\omega)/\kappa_{-} $ of all three families' dominant modes decreases to some finite values with$ \widetilde{\alpha} $ increasing toward the upper bound.When
$ \varLambda = 3>\varLambda_{\rm{c}} $ , the upper right panel of Fig. 1 shows that there is a lower bound on$ \widetilde{\alpha} $ with fixed$ Q/Q_{ \rm{ext}} $ and a possible lower bound on Q with fixed$ \widetilde{\alpha} $ . The black hole with the minimum value of$ \widetilde{\alpha} $ or Q (e.g. point B in Fig. 1) corresponds to the Nariai limit. The WKB method gives a small width and peak of the potential in the near Nariai regime, which makes QNMs vanish in the Nariai limit [23, 60, 61]. On the other hand, the surface gravity$ \kappa_{-} $ at the Cauchy horizon remains finite in the Nariai limit, which makes$ \beta = 0 $ for a Nariai black hole. So it is expected that$ \beta = 0 $ at the minimum values of$ Q/Q_{ \rm{ext}} $ and$ \widetilde{\alpha} $ in the lower left panel of Fig. 3(a) and the lower row of Fig. 3(b), respectively. Consequently, SCC is always valid around the Nariai limit. Therefore when$ \varLambda>\varLambda_{\rm{c}} $ , even for a 5-dimensional highly near-extremal EMGBdS black hole, SCC is always saved as long as$ \widetilde{\alpha} $ is close enough to its minimum value.We display the density plots of
$ \beta $ for 5-dimensional EMGBdS black holes with$ \varLambda = 1 $ and$ \varLambda = 3 $ in Fig. 5. SCC is violated in the regions between the extremal lines (dashed orange lines) and the threshold$ \beta = 1/2 $ (solid black lines). The$ Q/Q_{ \rm{ext}} = 0.9 $ line in red shows that, in both cases with$ \varLambda = 1 $ and$ \varLambda = 3 $ , SCC is respected at small$ \widetilde{\alpha} $ but violated when$ \widetilde{\alpha} $ is large enough. For a more extremal black hole (e.g.,$ Q/Q_{ \rm{ext}} = 0.99 $ ), SCC could be always violated in the$ \varLambda = 1 $ case. However when$ \varLambda = 3 $ , SCC can be recovered even for a highly near-extremal EMGBdS black hole in the region close to the Nariai line (dashed green lines).
Figure 5. (color online) Density plots of
$ \beta $ for a neutral massless scalar field in a 5-dimensional EMGBdS black hole with$ \varLambda = 1 $ (upper row) and$ \varLambda = 3 $ (lower row). The parameter space of interest is bounded by the Nariai limit (dashed green lines) and the extremal limit (dashed orange lines). The solid black lines represent the threshold$ \beta = 1/2 $ . SCC is valid in the regions below the solid black lines. When$ Q/Q_{ \rm{ext}} = 0.9 $ , SCC is saved at small$ \widetilde{\alpha} $ but violated at large$ \widetilde{\alpha} $ for both$ \varLambda = 1 $ and$ \varLambda = 3 $ . When$ Q/Q_{ \rm{ext}} = 0.99 $ , SCC is violated in all range of$ \widetilde{\alpha} $ for$ \varLambda = 1 $ but can be saved when$ \widetilde{\alpha} $ is small enough for$ \varLambda = 3 $ .Unlike the RNdS case [23], the insets in Fig. 3(a) show that there exist some near-extremal regions where the dominant NE mode dominates and has
$ {\rm{ Im}}(\omega)/\kappa_{-}<-1 $ (i.e.$ \beta>1 $ ), which indicates the violation of SCC in the$ C^{2} $ version. Moreover, our numerical results in the table in Fig. 6 suggest that$ {\rm{ Im}}(\omega)/\kappa_{-} $ for the dominant NE mode would approach$ -1 $ (i.e.,$ \beta\rightarrow1 $ ) in the extremal limit. In the density plot of$ \beta $ displayed in Fig. 6,$ \beta>1 $ and hence the$ C^{2} $ version of SCC is violated in the region between the solid black line and the dashed orange line. Additionally, the insets in Fig. 3(b) show that when$ Q/Q_{ \rm{ext}} = 1-10^{-2} $ and$ Q/Q_{ \rm{ext}} = 1-10^{-3}, $ the$ C^{2} $ version of SCC can be violated for a large enough value of$ \widetilde{\alpha} $ , which means that GB term also tends to violate SCC in the$ C^{2} $ version.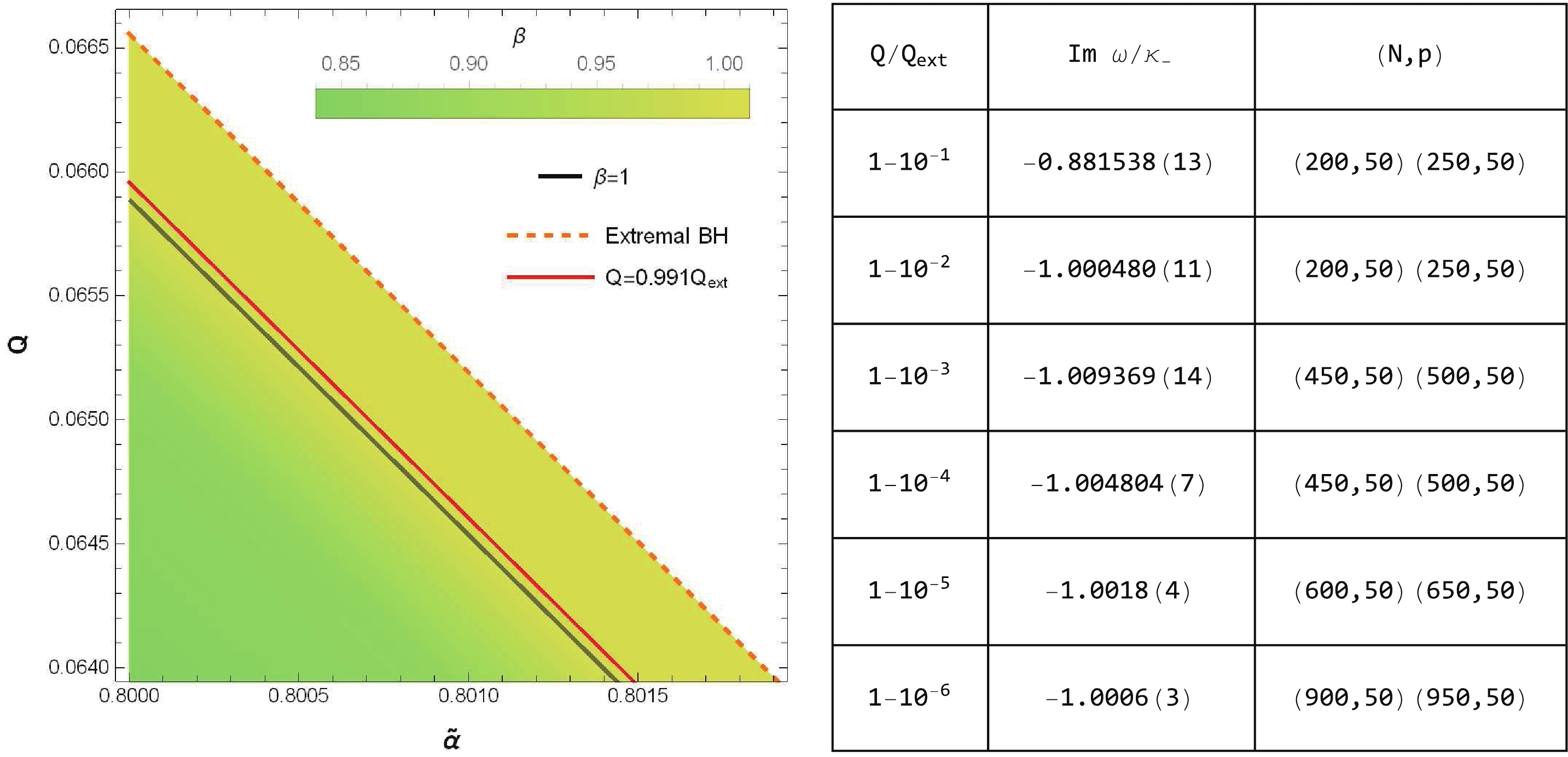
Figure 6. (color online) Left: Density plot of
$ \beta $ in a near-extremal region around$ \widetilde{\alpha} = 0.8 $ with$ \varLambda = 1 $ for$ d = 5 $ . The solid black line corresponds to$ \beta = 1 $ . In the region between the solid black line and the extremal limit (dashed orange line), the$ C^{2} $ version of SCC is violated for a near-extremal EMGBdS black hole, e.g.,$ Q/Q_{ \rm{ext}} = 0.991 $ shown by the red line. Right: A table of$ {\rm{ Im}}(\omega)/\kappa_{-} $ for the dominant NE modes for various near-extremal values of$ Q/Q_{ \rm{ext}} $ with$ \varLambda = 1 $ and$ \widetilde{\alpha} = 0.8 $ . The numbers in brackets in the second column indicate the number of agreed digits after the decimal point. In the third column, we show the different grid sizes and precisions$ (N,p) $ used in the computations. -
We now consider QNMs for a scalar field in a
$ 6 $ -dimensional EMGBdS black hole and investigate the validity of SCC. Since the allowed regions in Fig. 1 are quite different for$ \varLambda = 5 $ and$ \varLambda = 10 $ , we will focus on these two cases. For the lowest-lying mode of the three families, their$ {\rm{ Im}}(\omega)/\kappa_{-} $ are depicted against$ Q/Q_{ \rm{ext}} $ for various values of$ \widetilde{\alpha} $ in Fig. 7. It seems that the ranges of$ Q/Q_{ \rm{ext}} $ in which SCC is violated first increase and then decrease with increasing$ \widetilde{\alpha} $ . Furthermore, we plot$ {\rm{ Im}}(\omega)/\kappa_{-} $ against$ \widetilde{\alpha} $ with fixed$ Q/Q_{ \rm{ext}} $ , for the three families' dominant modes, in Fig. 7(b). When$ \varLambda = 5<\varLambda_{\rm{c}} $ , one has$ \widetilde{\alpha}\geqslant 0 $ . However, when$ \varLambda = 10>\varLambda_{\rm{c}} $ , there exists a positive lower bound on$ \widetilde{\alpha} $ , which can be observed in the lower row of Fig. 7(b). Since the lower bound corresponds to the Nariai limit, SCC is always valid close to the lower bound. Figure 7(b) shows that, as$ \widetilde{\alpha} $ increases from its minimum value,$ {\rm{ Im}}(\omega)/\kappa_{-} $ first decreases, for all three families' dominant modes, and then the dS and NE modes increase to zero (as shown in the insets of Fig. 7(b)) while the PS mode increases to some negative constant. Therefore SCC is always valid as long as$ \widetilde{\alpha} $ is large enough. Moreover, the SCC violation regions in Fig. 7(b) expand with increasing$ Q/Q_{ \rm{ext}} $ , which indicates that SCC tends to be violated for a black hole closer to extremality.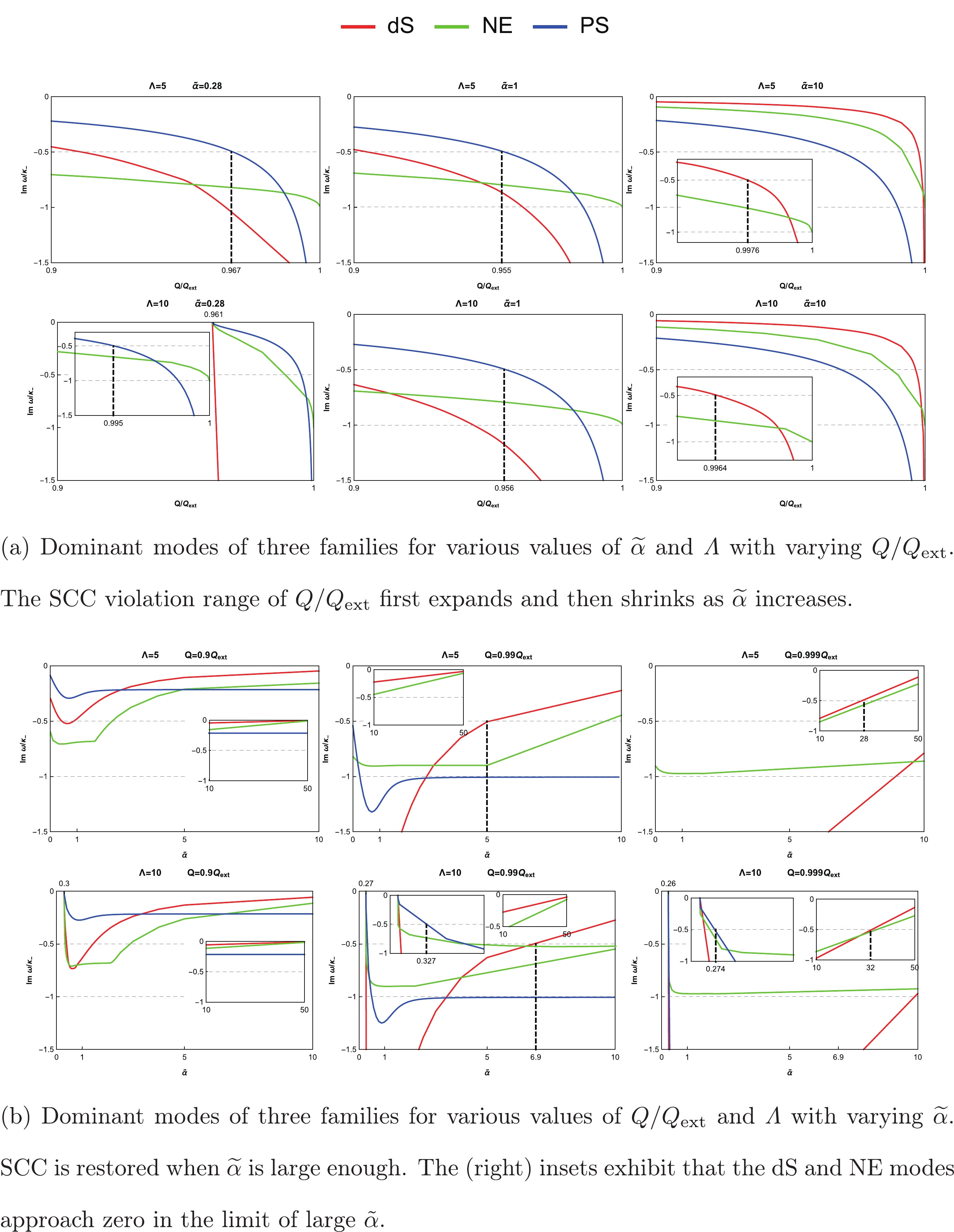
Figure 7. (color online) Dominant modes of three families for a neutral massless scalar field in a
$ 6 $ -dimensional EMGBdS black hole. The thick vertical dashed lines designate the points where$ \beta = 1/2 $ .The density plots of
$ \beta $ for 6-dimensional EMGBdS black holes with$ \varLambda = 5 $ and$ \varLambda = 10 $ are displayed in Fig. 8, where SCC is violated in the regions between the extremal limit (dashed orange lines) and the threshold$ \beta = 1/2 $ (solid black lines). For a near-extremal black hole with$ Q/Q_{ \rm{ext}} = 0.99 $ and$ \varLambda = 5<\varLambda_{\rm{c}} $ (the red line), the upper row of Fig. 8 shows that SCC is violated for small$ \widetilde{\alpha} $ , but can be restored when$ \widetilde{\alpha}\gtrsim 5.2 $ . When$ \varLambda = 10>\varLambda_{\rm{c}} $ , the lower left panel of Fig. 8 highlights the parameter space around the lower bound on$ \widetilde{\alpha} $ (point A), which shows that SCC is always valid when black holes approach the Nariai limit. In the lower right panel of Fig. 8, we plot the SCC violation region (yellow region) in the$ \widetilde{\alpha}\text{-}Q/Q_{ \rm{ext}} $ plane for a$ 6 $ -dimensional EMGBdS black hole with$ \varLambda = 5 $ . It shows that the$ Q/Q_{ \rm{ext}} $ range of the SCC violation region first increases and then decreases as$ \widetilde{\alpha} $ increases. Finally, we present the$ {\rm{ Im}}(\omega)/\kappa_{-} $ of the dominant NE modes for various near-extremal values of$ Q/Q_{ \rm{ext}} $ with different$ \varLambda $ and$ \widetilde{\alpha} $ in Table 1. Although we do not calculate$ {\rm{ Im}}(\omega)/\kappa_{-} $ in the very near-extremal regime due to the significant computational resource requirements, our findings infer that$ \beta $ may approach$ 1 $ from below in the extremal limit, which implies that the$ C^{2} $ version of SCC seems to be respected in the$ d = 6 $ case.$ \widetilde{\alpha} $ 

$ \varLambda $ 

$ Q/Q_{ \rm{ext}} $ 

$ {\rm{ Im}}(\omega)/\kappa_{-} $ 

$ (N,p) $ 

$ 1 $ 

$ 1 $ 

$ 1-10^{-4} $ 

$ -0.992860(6) $ 

$ (350,50)(400,50) $ 

$ 1-10^{-5} $ 

$ -0.9979(3) $ 

$ (450,50)(500,50) $ 

$ 1-10^{-6} $ 

$ -0.99939(4) $ 

$ (850,50)(900,50) $ 

$ 5 $ 

$ 1-10^{-4} $ 

$ -0.992449(6) $ 

$ (250,50)(300,50) $ 

$ 1-10^{-5} $ 

$ -0.9977(4) $ 

$ (350,50)(400,50) $ 

$ 1-10^{-6} $ 

$ -0.9993(4) $ 

$ (600,50)(650,50) $ 

$ 10 $ 

$ 1-10^{-4} $ 

$ -0.9918(4) $ 

$ (160,50)(200,50) $ 

$ 1-10^{-5} $ 

$ -0.9975(4) $ 

$ (300,50)(350,50) $ 

$ 1-10^{-6} $ 

$ -0.9992(4) $ 

$ (400,50)(450,50) $ 

Table 1.
$ {\rm{ Im}}(\omega)/\kappa_{-} $ of the dominant NE modes for$ 6 $ -dimensional EMGBdS black holes with various values of$ \widetilde{\alpha} $ and$ \varLambda $ , suggesting that$ \beta<1 $ in the highly near-extremal case.
Figure 8. (color online) Upper row: Density plots of
$ \beta $ for a neutral massless scalar field in a$ 6 $ -dimensional EMGBdS black hole with$ \varLambda = 5 $ . The SCC violation regions are between$ \beta = 1/2 $ (solid black lines) and the extremal limit (orange dashed lines). The insets shows that the$ Q/Q_{ \rm{ext}} = 0.99 $ line (red line) exits the SCC violation region around$ \widetilde{\alpha}\gtrsim 5.2 $ . Lower left: Density plots of$ \beta $ in a$ 6 $ -dimensional EMGBdS black hole with$ \varLambda = 10>\varLambda_{\rm{c}} $ around the minimum value of$ \widetilde{\alpha} $ . SCC is always saved close enough to the Nariai limit (dashed green lines). Lower right: The yellow region denotes the violation of SCC in a$ 6 $ -dimensional EMGBdS black hole with$ \varLambda = 5 $ while SCC is respected in the light green region. The tiny yellow region indicates that the violation of the SCC only occurs in a near-extremal black hole. Moreover, it shows that the range of$Q/Q_{\rm ext}$ where SCC is violated first increases and then decreases with increasing$ \widetilde{\alpha} $ . -
In this paper, we investigated the validity of SCC for a linear neutral massless scalar perturbation in
$ 5 $ - and$ 6 $ -dimensional EMGBdS black holes. In Sec. II, we obtained the allowed parameter regions where a EMGBdS black hole can have a Cauchy horizon for various$ \varLambda $ . After the method to calculate QNMs was discussed in Sec. III, the numerical results were presented in Sec. IV.For the EMGBdS black holes in the allowed region, there are two limits, namely the extremal limit and the Nariai limit. In the extremal limit, we found numerically that
$ \beta\rightarrow1 $ , and hence SCC is always violated. However in the Nariai limit, we showed that$ \beta\rightarrow0 $ , and hence SCC is always valid. When$ \varLambda>\varLambda_{\rm{c}} $ , the GB parameter$ \widetilde{\alpha} $ was found to have a positive lower bound, which corresponds to the Nariai black hole. So SCC is respected near the lower bound on$ \widetilde{\alpha} $ . On the other hand, there is an upper bound on$ \widetilde{\alpha} $ in the$ d = 5 $ case while no upper bound is imposed on$ \widetilde{\alpha} $ in the$ d = 6 $ case. Our numerical results showed that SCC tends to be violated/saved when$ \widetilde{\alpha} $ is large enough in the$ d = 5 $ /$ d = 6 $ case, which implies the GB term tends to worsen/alleviate the violation of SCC in the$ d = 5 $ /$ d = 6 $ case. We summarize the results for how the validity of SCC depends on$ \widetilde{\alpha} $ in Table 2, which indicates that the GB term plays a different role in the validity of SCC for a$ 5 $ -dimensional EMGBdS black hole than it does for a$ 6 $ -dimensional one.SCC violation range of $ Q/Q_{ \rm{ext}} $ with fixed

$ \widetilde{\alpha} $ 

Varying $ \widetilde{\alpha} $ with fixed

$ Q/Q_{ \rm{ext}} $ 

$ d=5 $ 

increases as $ \widetilde{\alpha} $ increases

SCC is violated near the maximum value of $ \widetilde{\alpha} $ 

$ d=6 $ 

first increases and then decreases as $ \widetilde{\alpha} $ increases

SCC is restored when $ \widetilde{\alpha} $ is large enough

Table 2. Dependence of the validity of SCC on the GB parameter
$\widetilde{\alpha}$ .We also checked the validity of the
$ C^{2} $ version of SCC for near-extremal EMGBdS black holes. In the$ d = 5 $ case, we found that in some parameter regions,$ \beta $ is allowed to exceed unity, which implies that the scalar is in$ C^{1} $ extension on the Cauchy horizon, and hence SCC is violated in the$ C^{2} $ version. Such violation leads to the existence of solutions with bounded Ricci curvature, corresponding to a much more severe failure of determinism in general relativity. However, the violation of SCC in the$ C^{2} $ version has not been observed in the$ d = 6 $ case. Furthermore, we found numerically that$ \beta\rightarrow1 $ in the extremal limit for both$ d = 5 $ and$ d = 6 $ . To our knowledge, the results of charged black holes in Einstein-Maxwell theory [23, 37], Einstein-Born-Infeld theory [42], Einstein-Logarithmic theory [43] and Horndeski theory [44] all suggest that the dominant mode of the NE family approaches$ 1 $ in the extremal limit. It is known that such a mode has been described analytically in asymptotically flat spacetime [36, 69, 70]. The reason why$ \beta\rightarrow1 $ in the extremal limit may relate to the fact that the extremal black holes share the same near-horizon topology, namely$ AdS_{2}\times S^{d-2} $ , leading to an enhanced spacetime symmetry [71-75].For EMGBdS black holes with
$ d>6 $ , we expect that the result might be similar to the$ d = 6 $ case, since their allowed regions are alike. In this paper, we only considered the scalar field perturbation of the fixed EMGBdS black hole background in the probe limit without taking into account the backreaction of the scalar field on the black hole spacetime. Our results on stability therefore actually refer to the scalar field rather than the EMGBdS black hole spacetime. In future studies, it will be very interesting to check the validity of SCC and discuss its dependence on the dimension d in a full backreaction way.Note: Just before this paper was submitted to arXiv, a relevant preprint [76] appeared, which investigated SCC in higher curvature gravity. In Ref. [76], it was found that the violation of SCC becomes worse as
$ \widetilde{\alpha} $ increases in the small$ \widetilde{\alpha} $ regime for both$ d = 5 $ and$ d = 6 $ , which is in agreement with our results. Similar to Ref. [76], we also observed that with$ \varLambda $ increasing, the PS mode crosses the$ \beta = 1/2 $ line at larger values of$Q/Q_{\rm ext}$ and becomes sub-dominant to the NE mode in the near-extremal regime. However, we carried out the analysis in a more thorough way with a broader survey of the parameter space and found that the behavior of SCC in EMGBdS black holes is much richer than what was observed in Ref. [76]. In particular, in the$\varLambda > \varLambda_{\rm crit}$ regime, we found that SCC can be restored for any arbitrary highly near-extremal black hole due to the presence of the Nariai limit, as shown in Figs. 5 and 8. Therefore we partially agree with the conclusion given in Ref. [76] that the presence of GB terms do not help to restore SCC. Moreover, our numerical results showed that the behavior of SCC is quite different in$ 5 $ - and$ 6 $ -dimensional cases. For instance, we found that the dominant modes of the three families decrease to some nonzero finite values towards the upper bound of$ \widetilde{\alpha} $ for$ d = 5 $ (see Fig. 4), while the dominant NE and dS modes tend to zero in the large$ \widetilde{\alpha} $ regime for$ d = 6 $ (see Fig. 7(b)). Besides, in the$ d = 6 $ case, we showed that the GB term tends to alleviate the violation of SCC in the large$ \widetilde{\alpha} $ regime, which was not explored in Ref. [76]. Finally, we investigated the$ C^{2} $ version of SCC, which was not studied in Ref. [76], and such violation was observed in a$ 5 $ -dimensional near-extremal EMGBdS black hole. -
We thank Guangzhou Guo and Shuxuan Ying for their helpful discussions and suggestions.
Strong cosmic censorship for a scalar field in an Einstein-Maxwell-Gauss-Bonnet-de Sitter black hole
- Received Date: 2020-07-30
- Accepted Date: 2020-09-30
- Available Online: 2021-02-15
Abstract: It has been shown that the Christodoulou version of the strong cosmic censorship (SCC) conjecture can be violated for a scalar field in a near-extremal Reissner-Nordstrom-de Sitter black hole. In this paper, we investigate the effects of higher derivative corrections to the Einstein-Hilbert action on the validity of SCC, by considering a neutral massless scalar perturbation in





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF



















 DownLoad:
DownLoad: