-
Identical pion intensity correlations (Bose-Einstein correlations, BECs) are important observables in high-energy heavy-ion collisions [1-6]. Because the multiplicity of identical pions in heavy-ion collisions at the Large Hadron Collider (LHC) is very high, multi-pion BEC analysis with high statistical accuracy has become possible [7, 8]. Recently, the ALICE Collaboration measured significant suppressions of three- and four-pion BECs for Pb-Pb collisions at
$ \sqrt{s_{NN}} = 2.76 $ TeV at the LHC [7, 8], suggesting considerable coherence between the particle-emitting sources produced in these collisions [7-11].Analysis of multi-pion BECs can provide more information about particle-emitting sources, compared with two-pion interferometry [4, 5, 7-36]. In particular, multi-pion BECs are sensitive to the source coherence [9-12, 26, 27]. In Refs. [10, 11], we investigated three- and four-pion BECs for a spherical evolving source of the pion gas with identical boson condensation. However, particle-emitting sources produced in relativistic heavy-ion collisions are anisotropic in space and may have complex structures. It is of interest to explain the experimental measurements of multi-pion BEC suppressions at the LHC using a more realistic model that can also explain the other observables in these collisions.
Event-wise, the initial systems produced in relativistic heavy-ion collisions strongly fluctuate in space. This initial fluctuation may yield inhomogeneous particle-emitting sources, in which there are hot spots and cold valleys. In Refs. [37-40], a granular source model was proposed and developed by Zhang et al., to explain the experimental results of two-pion interferometry at the Relativistic Heavy Ion Collider (RHIC) and LHC [41-45]. In Refs. [46-48], a granular source model was used to systemically study the pion transverse-momentum spectra, elliptic flows, and two-pion BECs in heavy-ion collisions, at the RHIC and LHC. The granular source model reproduced the experimental data of the pion transverse-momentum spectra, elliptic flows, and two-pion interferometry radii [46-48]. Considering that identical pions are emitted from droplets in the granular source model, and considering that the droplet radii are much smaller than the source size, the pion emission from one droplet is perhaps coherent in the case of high pion event multiplicity, owing to the condensation of identical bosons [10, 11, 49, 50].
In this work, we consider a granular source with coherent pion-emission droplets. The droplets in the granular source move with anisotropic velocities and evolve according to viscous hydrodynamics, as described in Ref. [48]. However, identical pion emissions from one droplet are assumed to be completely or partially coherent. We investigate multi-pion BECs in the granular source model with coherent pion-emission droplets. The normalized three- and four-pion correlation functions of granular sources are examined for completely coherent and momentum-dependent partially coherent pion emissions from one droplet.
The rest of this paper is organized as follows. In Sec. II, we examine the three- and four-pion BEC functions for a static granular source with coherent pion-emission droplets. In Sec. III, we investigate the three- and four-pion BECs in the granular source model, in which droplets evolve according to viscous hydrodynamics. We also investigate the normalized multi-pion correlation functions of evolving granular sources in this section. Finally, we provide a summary and discussion in Sec. IV.
-
We first consider a static granular source in which identical pions are emitted from separated droplets. The spatial distribution of the emitting points for each droplet is assumed to be Gaussian, i.e.,
$ \sim\!{\rm e}^{r^2/(2r_d^2)} $ , and the droplet centers$ R_j\; (j = 1,2, \cdots,n) $ are distributed in the granular source with a Gaussian distribution$ \sim\!{\rm e}^{-R_j^2/2R_G^2} $ . The two- and three-pion BEC functions for a static granular source can be expressed as [51, 52]$ C_2({{p}}_1,{{p}}_2) = 1+\frac{1}{n}{\rm e}^{-q_{12}^2 r_d^2}+\bigg(1-\frac{1}{n}\bigg) {\rm e}^{-q_{12}^2 (r_d^2+R_G^2)} \equiv 1+\frac{1}{n} {\cal{R}}^d(1,2)+\bigg(1 -\frac{1}{n}\bigg){\cal{R}}^G(1,2), $

(1) $ \begin{aligned}[b] C_3({{p}}_1,{{p}}_2,{{p}}_3) =& 1+\frac{1}{n}\bigg[{\cal{R}}^d(1,2)+{\cal{R}}^d(1,3) +{\cal{R}}^d(2,3)\bigg]+\bigg(1-\frac{1}{n}\bigg)\bigg[{\cal{R}}^G(1,2) +{\cal{R}}^G(1,3)+{\cal{R}}^G(2,3)\bigg] \\& +\frac{2}{n^2}\bigg[{\cal{R}}^d(1,2){\cal{R}}^d(1,3){\cal{R}}^d(2,3) \bigg]^{\frac{1}{2}}+\frac{2(n-1)}{n^2}\bigg[\Big({\cal{R}}^d(1,3){\cal{R}}^d(2,3)/ {\cal{R}}^d(1,2)\Big)^{\!\frac{1}{2}}{\cal{R}}^G(1,2)\\ &+\Big({\cal{R}}^d(1,2){\cal{R}}^d(2,3)/{\cal{R}}^d(1,3)\Big)^{\!\frac{1}{2}}{\cal{R}}^G(1,3)+\Big({\cal{R}}^d(1,2){\cal{R}}^d(1,3)/ {\cal{R}}^d(2,3)\Big)^{\!\frac{1}{2}}{\cal{R}}^G(2,3)\bigg]\\ &+\frac{2(n-1)(n-2)}{n^2}\bigg[{\cal{R}}^G(1,2){\cal{R}}^G(1,3) {\cal{R}}^G(2,3)\bigg]^{\frac{1}{2}}, \end{aligned} $

(2) where n is the droplet number in the granular source,
$ {\cal{R}}^d(1,2) = {\rm e}^{-{{q}}_{12}^2 r_d^2} $ ,$ {\cal{R}}^G(1, 2) = {\rm e}^{-{{q}}_{12}^2 (r_d^2+R_G^2)} $ , and${{q}}_{ij} = {{p}}_i- $ $ {{p}}_j\; (i,j = 1,2,3,4) $ . In Eq. (1), the$ {\cal{R}}^d(1,2) $ and$ {\cal{R}}^G(1,2) $ terms express the correlations between two pions emitted from one droplet and different droplets, respectively. In Eq. (2), the$ \dfrac{2}{n^2}[\,\cdots\,] $ and$ \dfrac{2(n-1)}{n^2}[\,\cdots\,] $ terms express the pure triplet correlations between three pions emitted from one droplet and two pions emitted from one droplet, respectively. In Eq. (2), the last term expresses the pure triplet correlations between three pions emitted from different droplets. The two- and three-pion correlation functions become those of the Gaussian sources when$ n\to\infty\; (r_d\to 0) $ . Similarly, one can obtain the four-pion correlation function for a static granular source, as described in Appendix A.For a small droplet radius, the pion emission from a droplet is significantly coherent [10, 11, 49, 50]. Assuming the pions emitted from one droplet are completely coherent, the two- and three-pion correlation functions for a granular source become
$ C_2({{p}}_1,{{p}}_2) = 1+\frac{(n-1)}{n}{\cal{R}}^G(1,2), $

(3) $\begin{aligned}[b] C_3({{p}}_1,{{p}}_2,{{p}}_3)\! =& \!1\!+\!\frac{(n-1)}{n}\bigg[{\cal{R}}^G(1,2) \!+\!{\cal{R}}^G(1,3)\!+\!{\cal{R}}^G(2,3)\bigg] \\ &+ \frac{2(n-1)(n-2)}{n^2} \bigg[{\cal{R}}^G(1,2){\cal{R}}^G(1,3){\cal{R}}^G(2,3)\bigg]^{\!\frac{1}{2}}. \end{aligned}$

(4) The four-pion correlation function for a granular source with completely coherent pion-emission droplets can be expressed as
$ \begin{aligned}[b] C_4({{p}}_1,{{p}}_2,{{p}}_3,{{p}}_4)\! =& \!1+\frac{(n-1)}{n}\bigg[{\cal{R}}^G(1,2) \!+\!{\cal{R}}^G(1,3)\!+\!{\cal{R}}^G(1,4)\!+\!{\cal{R}}^G(2,3)\!+\!{\cal{R}}^G (2,4)\!+\!{\cal{R}}^G(3,4)\bigg] \\ &+\frac{2(n-1)(n-2)}{n^2}\bigg[\bigg({\cal{R}}^G(1,2){\cal{R}}^G(1,3) {\cal{R}}^G(2,3)\bigg)^{\!\frac{1}{2}}\!+\!\bigg({\cal{R}}^G(1,2){\cal{R}}^G(1,4) {\cal{R}}^G(2,4)\bigg)^{\!\frac{1}{2}}\\ &+\bigg({\cal{R}}^G(2,3){\cal{R}}^G(2,4){\cal{R}}^G(3,4) \bigg)^{\!\frac{1}{2}}\!+\!\bigg({\cal{R}}^G(1,3){\cal{R}}^G(1,4) {\cal{R}}^G(3,4)\bigg)^{\!\frac{1}{2}}\bigg]\\ &+\frac{(n\!-\!1)(n\!-\!2)(n\!-\!3)}{n^3}\bigg[{\cal{R}}^G(1,2) {\cal{R}}^G(3,4)\!+\!{\cal{R}}^G(1,3){\cal{R}}^G(2,4)\!+\!{\cal{R}}^G(2,3){\cal{R}}^G(1,4) \bigg]\\ &+\frac{(n-1)}{n^3}\bigg[{\cal{R}}^G(1,2){\cal{R}}^G(3,4)\bigg({\rm e}^{-2{{q}}_{12}\cdot{{q}}_{34} R_G^2} +{\rm e}^{-2{{q}}_{12}\cdot{{q}}_{43}R_G^2}\bigg) +{\cal{R}}^G(1,3){\cal{R}}^G(2,4) \\ & \times \bigg({\rm e}^{-2{{q}}_{13}\cdot{{q}}_{24}R_G^2} +{\rm e}^{-2{{q}}_{13}\cdot{{q}}_{42}R_G^2}\bigg) +{\cal{R}}^G(1,4){\cal{R}}^G(2,3)\bigg({\rm e}^{-2{{q}}_{14}\cdot{{q}}_{23}R_G^2} +{\rm e}^{-2{{q}}_{14}\cdot{{q}}_{32}R_G^2}\bigg)\bigg] \\ &+\frac{2(n-1)(n-2)}{n^3}\bigg[{\cal{R}}^G(1,2){\cal{R}}^G(3,4)\bigg( {\rm e}^{-{{q}}_{12}\cdot{{q}}_{34}R_G^2} +{\rm e}^{-{{q}}_{12}\cdot{{q}}_{43}R_G^2}\bigg) +{\cal{R}}^G(1,3){\cal{R}}^G(2,4) \\ & \times \bigg({\rm e}^{-{{q}}_{13}\cdot{{q}}_{24}R_G^2} +{\rm e}^{-{{q}}_{13}\cdot{{q}}_{42}R_G^2}\bigg) +{\cal{R}}^G(1,4){\cal{R}}^G(2,3)\bigg({\rm e}^{-{{q}}_{14}\cdot{{q}}_{23}R_G^2} +{\rm e}^{-{{q}}_{14}\cdot{{q}}_{32}R_G^2}\bigg)\bigg] \\ &+\frac{2(n-1)(n-2)(n-3)}{n^3}\bigg[\bigg({\cal{R}}^G(1,2){\cal{R}}^G(2,3){\cal{R}}^G(3,4){\cal{R}}^G(1,4)\bigg)^{\!\frac{1}{2}}\\ &+\bigg({\cal{R}}^G(1,3){\cal{R}}^G(2,3){\cal{R}}^G(2,4){\cal{R}}^G(1,4)\bigg)^{\!\frac{1}{2}}\!+\!\bigg({\cal{R}}^G(1,2){\cal{R}}^G(2,4) {\cal{R}}^G(3,4){\cal{R}}^G(1,3)\bigg)^{\!\frac{1}{2}}\bigg], \end{aligned} $

(5) where the third pair of square brackets expresses the correlations of double pion pairs where four pions are emitted from four different droplets; the fourth pair of square brackets expresses the correlations of double pion pairs where the two pions of a pair are emitted from two different droplets and the two pions of another pair are emitted respectively from the two droplets as well; the fifth pair of square brackets expresses the correlations of double pion pairs where the two pions of a pair are emitted from two different droplets and the two pions of another pair are emitted respectively from one of the same droplets and from another droplet; and the last pair of square brackets expresses the pure quadruplet pion correlations where four pions are emitted from four different droplets. A detailed derivation of the correlation function is given in Appendix A.
In Figs. 1(a) and 1(b), we plot the two-pion correlation functions of static granular sources with chaotic and completely coherent pion-emission droplets, respectively. In Figs. 1(d) and 1(e), we plot the three-pion correlation functions of static granular sources with chaotic and completely coherent pion-emission droplets, respectively. In Figs. 1(g) and 1(h), we plot the four-pion correlation functions of static granular sources with chaotic and completely coherent pion-emission droplets, respectively. The panels (c), (f), and (i) show the ratios of the correlation functions of granular sources with completely coherent pion-emission droplets to the correlation functions of granular sources with chaotic pion-emission droplets. Here, the radii of the granular sources were set to
$ R_G = 6.0 $ fm. The variable$ Q_m\; (m = 2,3,\cdots) $ is defined by the covariant relative momenta, as follows:
Figure 1. (color online) Two-, three-, and four-pion correlation functions for static granular sources with chaotic (top panels) and completely coherent (middle panels) pion-emission droplets. Here, the radii of the granular sources were RG = 6.0 fm. The bottom panels show the ratios of the correlation functions for the granular sources with completely coherent droplets to those for the granular sources with chaotic droplets.
$ Q_m = \sqrt{\sum\limits_{i<j\leqslant m}-(p_i-p_j)^\mu (p_i-p_j)_\mu}, \; \; \; \; (m\geqslant 2). $

(6) From Fig. 1, it is evident that the intercepts of the correlation functions for granular sources with completely coherent droplets decrease, compared with those for granular sources with chaotic droplets. The intercept reductions decrease with increasing droplet number n. The intercept for the four-pion correlation function decreases much more than those for the two- and three-pion correlation functions, for the same droplet number n. From the ratio results, the correlation functions for completely coherent droplets exhibit more decreases for smaller droplets in the high relative-momentum variable regions.
The normalized three-pion correlation function
$ r_3 $ is defined by the ratio of the three-pion cumulant correlator to the square root of the product of the two-particle correlators [26, 27]. For a granular source with completely coherent pion-emission droplets, it is given by$ r_3(Q_3) = \frac{[c_3(Q_3)-1][n/(n-1)]^{3/2}} {\sqrt{{\cal{R}}^G(1,2)\!(Q_3){\cal{R}}^G(2,3)\!(Q_3){\cal{R}}^G(1,3)\!(Q_3)}}, $

(7) where
$ \begin{aligned}[b] c_3(Q_3) =& 1+\frac{2(n-1)(n-2)}{n^2}\\& \times \bigg[{\cal{R}}^G(1,2){\cal{R}}^G(1,3){\cal{R}}^G(2,3) \bigg]^{\!\frac{1}{2}}\!\!\!(Q_3). \end{aligned} $

(8) Because
$ r_3 $ is insensitive to the resonance decay, it is used for measuring the source coherence in analyses of experimental data [7, 30-34]. Similarly, the normalized four-pion correlation function$ r_4 $ of a granular source is given by$ r_4(Q_4) \!=\! \frac{[c_4(Q_4)-1][n/(n-1)]^2}{\sqrt{{\cal{R}}^G(\!1,2\!)\!(Q_4){\cal{R}}^G(\!2,3\!)\!(Q_4) {\cal{R}}^G(\!3,4\!)\!(Q_4){\cal{R}}^G(\!1,4\!)\!(Q_4)}}, $

(9) where
$ \begin{aligned}[b] c_4(Q_4) =& 1+\frac{2(n-1)(n-2)(n-3)}{n^3}\\& \times\bigg[\bigg({\cal{R}}^G(1,2){\cal{R}}^G(2,3) {\cal{R}}^G(3,4){\cal{R}}^G(1,4)\bigg)^{\!\frac{1}{2}}(Q_4)\\& +\bigg({\cal{R}}^G(1,3){\cal{R}}^G(2,3){\cal{R}}^G(2,4){\cal{R}}^G(1,4)\bigg)^{\!\frac{1}{2}}(Q_4)\\& +\bigg({\cal{R}}^G(1,2){\cal{R}}^G(2,4){\cal{R}}^G(3,4) {\cal{R}}^G(1,3)\bigg)^{\!\frac{1}{2}}(Q_4)\bigg]. \end{aligned} $

(10) In Figs. 2(a) and 2(b), we plot the normalized three- and four-pion correlation functions
$ r_3(Q_3) $ and$ r_4(Q_4) $ for static granular sources with completely coherent pion-emission droplets, respectively. The parameters of the granular sources are the same as in Fig. 1. The normalized correlation functions exhibit plateaus in the low-$ Q_{3,4} $ region, up to$ \sim\!50 $ MeV/c. We plot the intercepts of$ r_3(Q_3) $ and$ r_4(Q_4) $ as functions of the droplet number in Fig. 3. The intercepts for the four-pion normalized correlation functions are more sensitive to the droplet number n than for the three-pion normalized correlation functions, in the$ 5<n<12 $ region.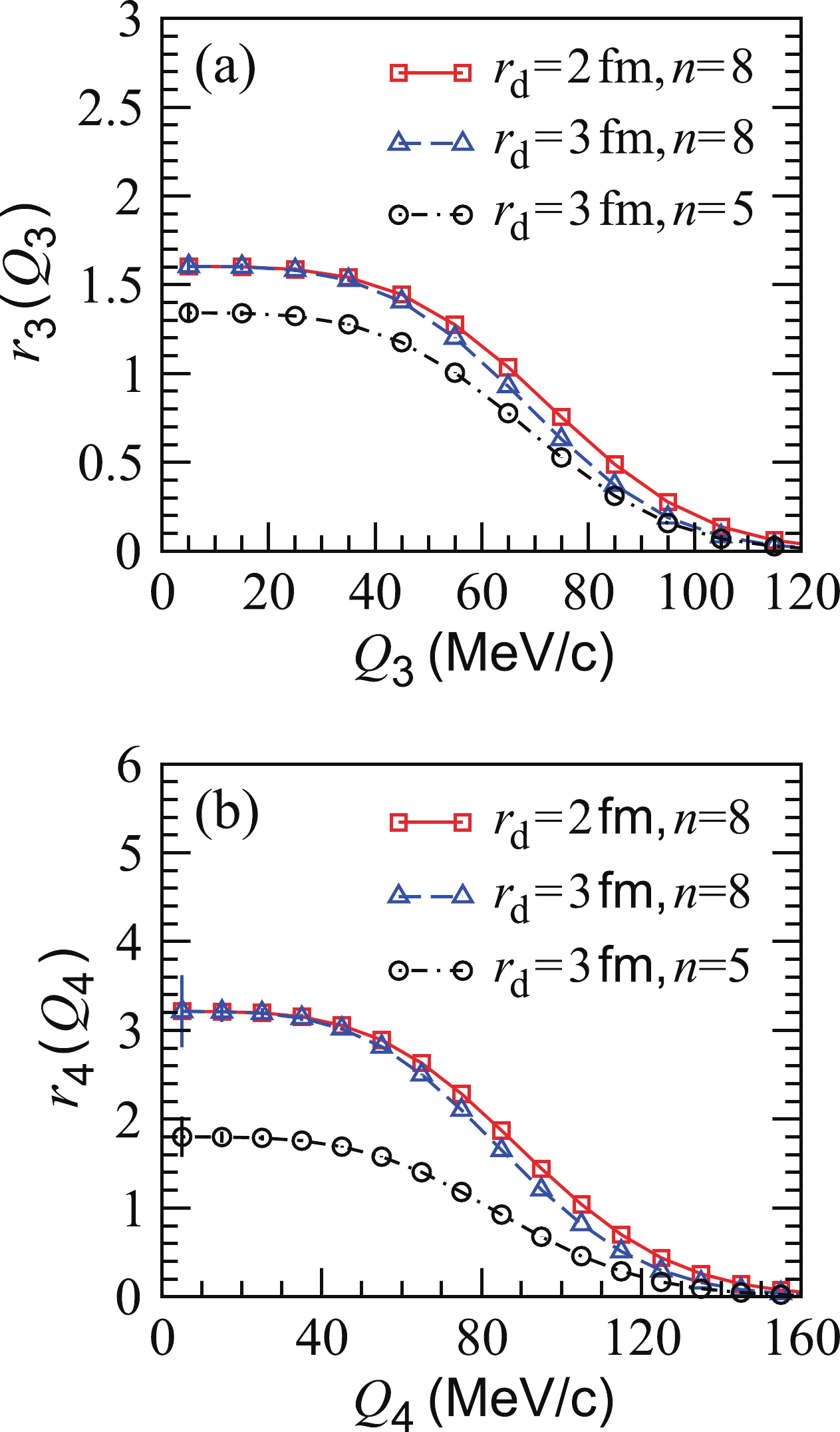
Figure 2. (color online) (a) Normalized three-pion correlation functions for static granular sources with completely coherent pion-emission droplets. (b) Normalized four-pion correlation functions for static granular sources with completely coherent pion-emission droplets. Parameters of the granular sources are the same as in Fig. 1.
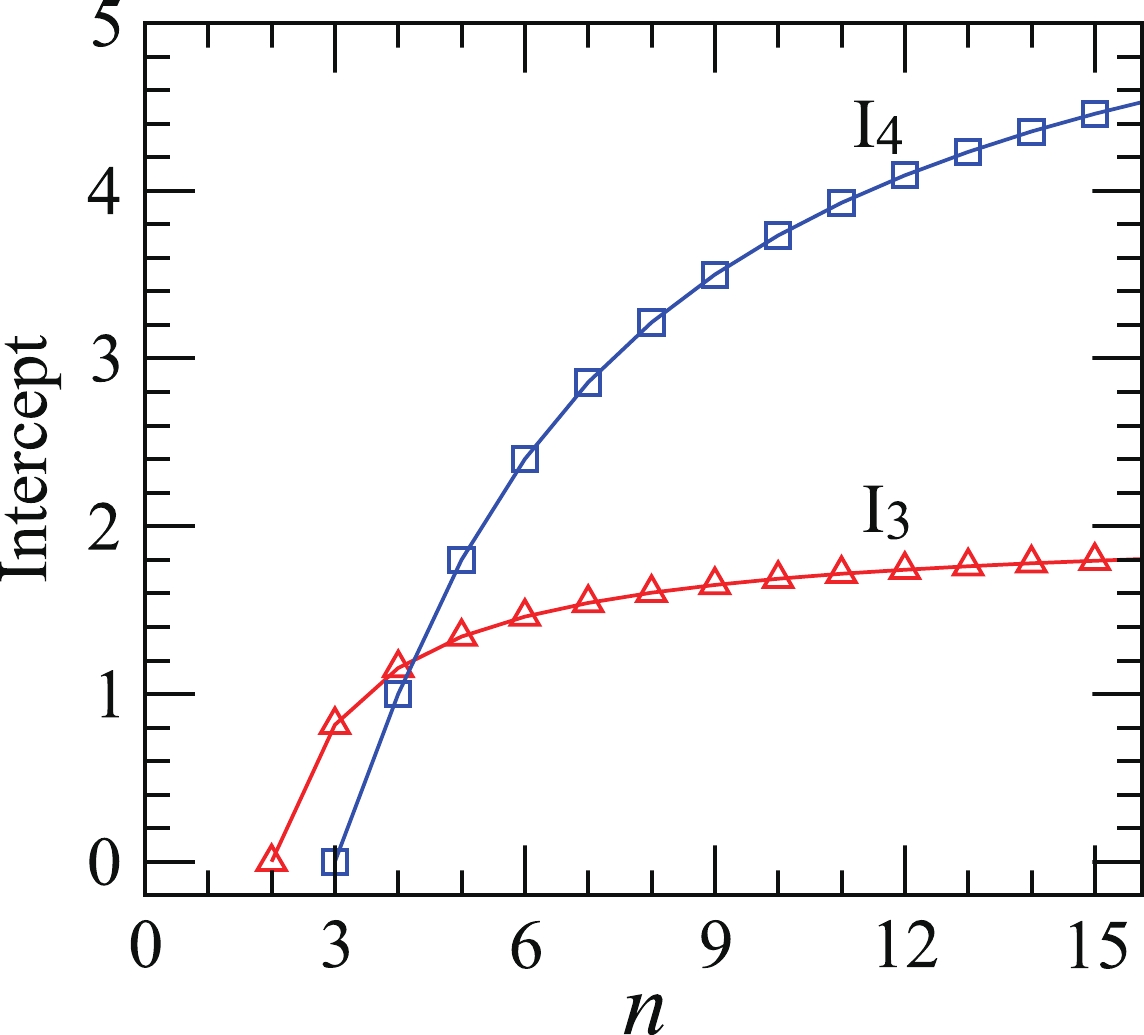
Figure 3. (color online) Intercepts of
$ r_3(Q_3)$ and$ r_4(Q_4)$ for granular sources with completely coherent pion-emission droplets, as functions of the droplet number for static granular sources.Owing to the lack of expansion, the three- and four-pion correlation functions of static granular sources fall rapidly with multi-pion relative momenta
$ Q_3 $ and$ Q_4 $ , respectively. It is difficult to describe the experimental data of multi-pion correlations using a static granular source model. In the next section, we study the three- and four-pion correlation functions in an evolving granular source model and compare the resulting multi-pion correlation functions with available experimental data. -
Evolving granular source models can reproduce the pion transverse-momentum spectra, elliptic flows, and interferometry radii [46-48]. In what follows, we study multi-pion BECs for evolving granular sources, in which droplets expand according to viscous hydrodynamics and emit pions coherently.
-
The model we consider is based on a viscous granular source model developed in Ref. [48], but presently, pions that are emitted from one droplet are assumed to be completely or partially coherent. In this subsection, we briefly present the components of the granular source model used in the work. For a detailed explanation of granular source models, the reader is referred to Refs. [38-40, 46-48].
The granular source model was proposed by W. N. Zhang et al. [37, 38], to explain the RHIC HBT puzzle,
$ R_{\rm{out}}/R_{\rm{side}}\; \sim\; 1 $ [41, 42, 47, 48], where$ R_{\rm{out}} $ and$ R_{\rm{side}} $ are two HBT radii in the transverse plane along and perpendicular to the transverse momentum of the particle pairs [53-55]. Because the HBT radius$ R_{\rm{out}} $ decreases with decreasing system lifetime, while the HBT$ R_{\rm{side}} $ increases with increasing system size, particle-emitting sources have small hot droplets; therefore, a short evolution time and distribution in a large space may yield$ R_{\rm{out}}/R_{\rm{side}}\; \sim\; 1 $ [37-40]. Although the early idea of constructing a granular source model was based on the first-order QCD transition, the occurrence of granular sources may not be limited to first-order phase transitions. In relativistic heavy ion collisions at the RHIC and LHC energies, large initial fluctuations and instabilities during the early violent expansion of the system may yield granular inhomogeneous structures of particle-emitting sources [38-40].The granular source model assumes that the initial spatial inhomogeneity and violent expansion during the early stages of the system produced in ultrarelativistic heavy-ion collisions may break up the system into many hot and dense droplets, leading to the formation of a granular particle-emitting source. During the formation of the initial granular source, the droplet centers are distributed within a cylinder along the collision axis, and the initial energy distribution in a droplet satisfies the Woods-Saxon distribution, as shown in Refs. [47, 48]. The average droplet number,
$ \langle n\rangle $ , of a granular source is related to the initial mean separation and geometry of the source [51].The evolution of a granular source includes the droplet evolution according to viscous hydrodynamics and the droplet expansion in its entirety, with anisotropic droplet velocities
$ v_{{\rm d}x} $ ,$ v_{{\rm d}y} $ , and$ v_{{\rm d}z} $ . In the granular source model, the geometry and velocity parameters are determined by comparing the model results for the pion transverse-momentum spectra, elliptic flows, and two-pion interferometry radii with experimental data. In this paper, we used the viscous granular source model developed in Ref. [48] to describe the source evolution for Pb-Pb collisions at$ \sqrt{s_{{NN}}} = 2.76 $ TeV [8], and the model parameters were the same as in [48]. -
In Figs. 4(a) and 4(b), we plot the three-pion correlation functions
$ C_3(Q_3) $ for evolving granular sources with completely coherent pion-emission droplets, for central Pb-Pb collisions at$ \sqrt{s_{{NN}}} = 2.76 $ TeV. The experimental data of$ C_3(Q_3) $ , measured by the ALICE Collaboration for central Pb-Pb collisions [8], are presented for comparison. Panels (a) and (b) show the results for the low- and high-transverse-momentum intervals$ 0.16< $ $ K_{T3} <0.3 $ GeV/c and$ 0.3<K_{T3}<1 $ GeV/c, respectively. Here,$ K_{T3} = |{{p}}_{T1} +{{p}}_{T2}+{{p}}_{T3}|/3 $ . The average droplet number$ \langle n\rangle $ for the simulation events with the granular source parameters determined together by the experimental data of transverse-momentum spectra, elliptic flows, and interferometry radii in 0%-10% Pb-Pb collisions [48] is 8. In Fig. 4, the results for$ \langle n\rangle = 9 $ and$ \langle n \rangle = 6 $ are shown, for the same granular source parameters but smaller and larger initial mean separations. The granular source results for the small-$ Q_3 $ region increase with the average droplet number$ \langle n\rangle $ . However, the results for$ \langle n\rangle = 8 $ are lower than the experimental data for the small-$ Q_3 $ region.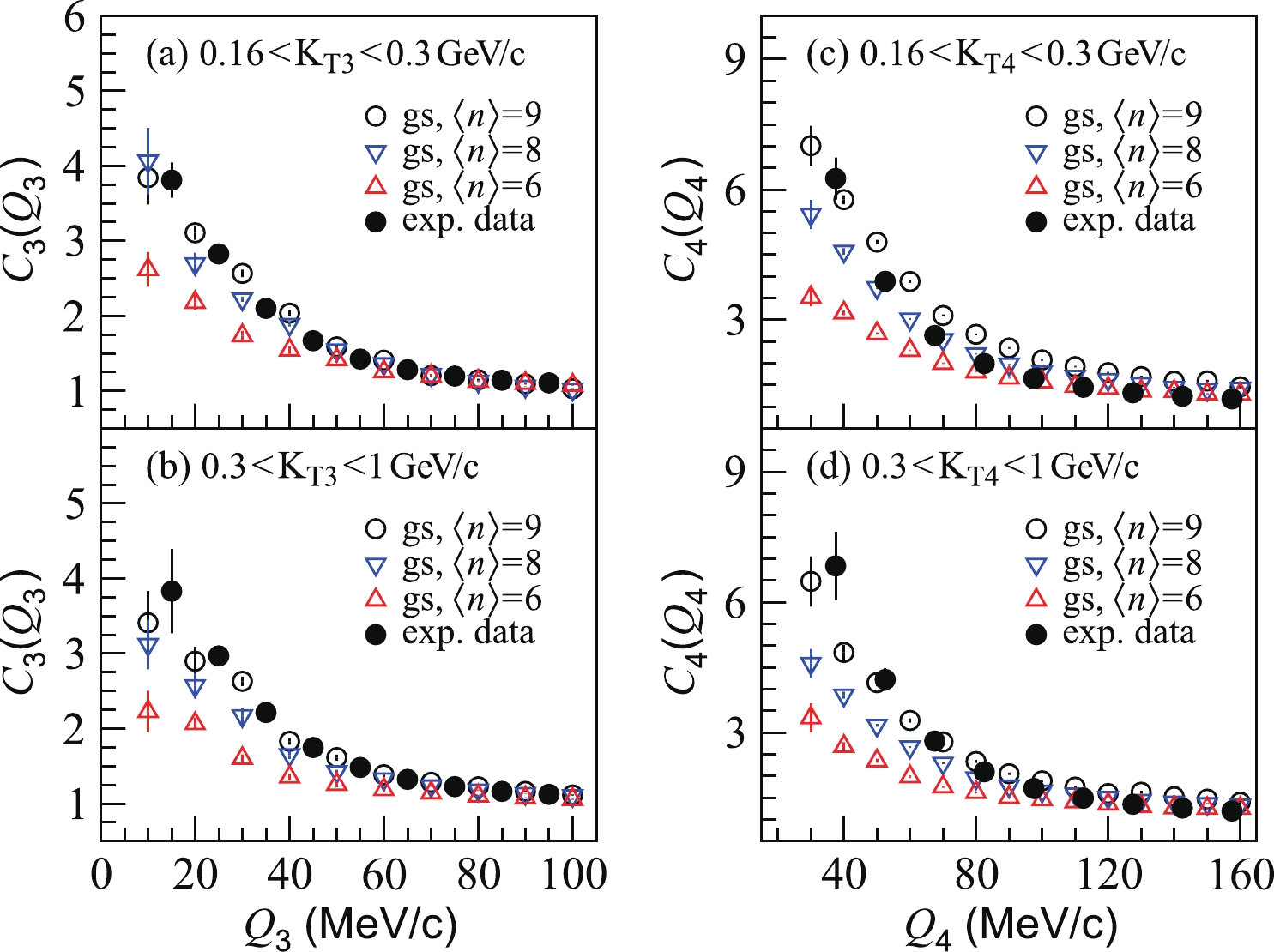
Figure 4. (color online) Three- and four-pion correlation functions for evolving granular sources with completely coherent droplets and experimental data for central Pb-Pb collisions at
$ \sqrt{s_{{NN}}} = 2.76 $ TeV [8], for transverse-momentum intervals$ 0.16<K_{T3}<0.3 $ GeV/c and$ 0.3<K_{T3}<1 $ GeV/c. Here,$ \langle n\rangle $ denotes the average droplet number for the considered evolving granular sources.In Fig. 4(c) and 4(d), we plot the four-pion correlation functions
$ C_4(Q_4) $ for evolving granular sources with completely coherent pion-emission droplets, for central Pb-Pb collisions at$ \sqrt{s_{{NN}}} = 2.76 $ TeV. The experimental data of$ C_4(Q_4) $ , measured by the ALICE Collaboration for central Pb-Pb collisions [8], are presented for comparison. Panels (a) and (b) show the results for the low and high transverse-momentum intervals$ 0.16<K_{T4} <0.3 $ GeV/c and$ 0.3<K_{T4}<1 $ GeV/c, respectively. Here,$ K_{T4} = |{{p}}_{T1} +{{p}}_{T2}+{{p}}_{T3}+{{p}}_{T4}|/4 $ . The four-pion correlation functions of the granular sources increase with the average droplet number$ \langle n \rangle $ , for the small-$ Q_4 $ region. In addition, the results for$ \langle n\rangle = 8 $ are lower than the experimental results for the small-$ Q_4 $ region. The multi-pion correlation functions are sensitive to the number of droplets in the granular sources. However, the transverse-momentum spectra and elliptic flows of the granular sources are insensitive to$ \langle n\rangle $ [46-48].Considering that pions with high momenta are more likely to be emitted chaotically from excited states [10, 11, 49, 50], we further studied multi-pion BECs for granular sources with partially coherent pion-emission droplets. We assumed that pions that are emitted from one droplet and have momenta below a fixed value
$ p' $ have coherent amplitudes and therefore do not exhibit intensity correlations. However, pions with momenta above$ p' $ result from chaotic emissions (from excited-states).In Figs. 5(a) and 5(b), we compare the three-pion correlation functions for evolving granular sources with completely coherent pion-emission droplets (corresponding to
$ p' = \infty $ ) and partially coherent pion-emission droplets with$ p' = $ 0.5 and 0.7 GeV/c, for the lower- and higher- transverse-momentum$ K_{T3} $ intervals, respectively. Here, the average droplet number of the granular sources is 8, and the solid-circle symbols indicate the experimental results for central Pb-Pb collisions at$ \sqrt{s_{{NN}}} = 2.76 $ TeV [8]. In the low-$ Q_3 $ region, the three-pion correlation increases with decreasing$ p' $ , and the increase is greater in the higher$ K_{T3} $ interval than in the lower$ K_{T3} $ interval. This is because the contribution of the chaotic pion emission to the correlation functions increases with decreasing$ p' $ , and pions with high momenta, which are more likely to be emitted chaotically, have higher$ K_{T3} $ than those with low momenta. The three-pion correlation functions for the granular source with$ p' = 0.5 $ GeV/c are approximately in agreement with the experimental data.
Figure 5. (color online) Three- and four-pion correlation functions for evolving granular sources with completely coherent (
$ p' = \infty $ ) and partially coherent ($ p' = $ 0.5 and 0.7 GeV/c) pion-emission droplets, for transverse-momentum intervals$ 0.16<K_{T3}<0.3 $ GeV/c and$ 0.3<K_{T3}<1 $ GeV/c. Here, the average droplet number of the granular sources is 8, and solid-circle symbols indicate experimental data for central Pb-Pb collisions at$ \sqrt{s_{{NN}}} = 2.76 $ TeV [8].In Figs. 5(c) and 5(d), we compare the four-pion correlation functions for evolving granular sources with completely coherent pion-emission droplets (corresponding to
$ p' = \infty $ ) and partially coherent pion-emission droplets with$ p' = $ 0.5 and 0.7 GeV/c, for the lower-and higher-transverse-momentum$ K_{T4} $ intervals, respectively. Here, the average droplet number of the granular sources is 8, and the solid-circle symbols indicate the experimental results for central Pb-Pb collisions at$ \sqrt{s_{{NN}}} = 2.76 $ TeV [8]. Compared with the three-pion correlation functions, the four-pion correlation functions of the considered granular sources are more sensitive to the value of$ p' $ but are inconsistent with the experimental data. This puzzle in the current framework indicates that partially coherent pion-emission should be given more attention, to make the model multi-pion correlation functions agreeable with experimental data. -
The normalized multi-pion correlation functions
$ r_3 $ and$ r_4 $ are believed to be suitable for analyzing the source coherence in relativistic heavy-ion collisions. In the preceding section, it was found that the normalized correlation functions are sensitive to the number of droplets in a static granular source with completely coherent pion-emission droplets. In this subsection, we investigate$ r_3 $ and$ r_4 $ for evolving granular sources with completely coherent and partially coherent pion-emission droplets.We show in Figs. 6(a) and 6(b) the normalized three-pion correlation functions for evolving granular sources with completely coherent pion-emission droplets and different average droplet numbers
$ \langle n\rangle $ , for the transverse-momentum intervals$ 0.16<K_{T3}<0.3 $ GeV/c and$ 0.3<K_{T3}<1 $ GeV/c, respectively. The normalized correlation function increases with$ \langle n\rangle $ , for both transverse-momentum intervals. Compared with the normalized three-pion correlation functions for static granular sources, shown in Fig. 2(a), which plateau in the small-$ Q_3 $ region, those for evolving granular sources with large$ \langle n\rangle $ values decrease with$ Q_3 $ for the small-$ Q_3 $ region. The decrease in$ r_3 $ with increasing$ Q_3 $ indicates that the three-pion cumulant correlator (correlation of pure pion-triplet interference) decreases more rapidly with increasing$ Q_3 $ than two-pion correlations.
Figure 6. (color online) (a) - (d) Normalized three- and four-pion correlation functions for evolving granular sources with completely coherent pion-emission droplets. (e) - (h) Normalized three and four-pion correlation functions of the evolving granular sources with partially coherent (
$ p' = $ 0.5 and 0.7 GeV/c) and completely coherent ($ p' = \infty $ ) pion-emission droplets for the average droplet number$ \langle n\rangle = 8 $ .We show in Figs. 6(c) and 6(d) the normalized four-pion correlation functions for evolving granular sources with completely coherent pion-emission droplets and different average droplet numbers
$ \langle n\rangle $ , for the transverse-momentum intervals$ 0.16<K_{T4}<0.3 $ GeV/c and$ 0.3<K_{T4}<1 $ GeV/c, respectively. The normalized correlation function increases with$ \langle n\rangle $ , for both transverse-momentum intervals. Compared with the normalized three-pion correlation functions for evolving granular sources, the four-pion correlation functions are more sensitive to$ \langle n\rangle $ .In Figs. 6(e) – 6(h), we compare the normalized three- and four-pion correlation functions for evolving granular sources with completely coherent (
$ p' = \infty $ ) and partially coherent ($ p' = $ 0.5 and 0.7 GeV/c) pion-emission droplets. Here, the average droplet number for the granular sources is 8. The normalized three-pion correlation functions increase slightly with decreasing$ p' $ . However, the intercepts of the correlation functions at$ Q_3\sim 0 $ are approximately in agreement, because the intercept is mainly determined by the droplet number in the granular source. The normalized four-pion correlation functions increase with decreasing$ p' $ . For the wide transverse-momentum interval,$ 0.3<K_{T4}<1 $ GeV/c, the normalized four-pion correlation function for the smallest$ p' $ is clearly higher at approximately$ Q_4\sim 100 $ MeV/c, owing to the momentum dependence of pion-emission coherence and the sensitivity of high-order pion correlations to the source coherence. As discussed in Ref. [11], the average pion momentum increases with increasing$ Q_4 $ if there are no other constraints. This leads to an increase in the chaotic emission possibility with increasing$ Q_4 $ and the enhancement of$ r_4(Q_4) $ in the middle-$ Q_4 $ region [see Fig. 7(d) in [11]]. This can be attributed to the notion that high-momentum pions are more likely emitted chaotically from excited states.Table 1 presents the results for
$ r_3(Q_3) $ and$ r_4(Q_4) $ at$ Q_3 = 10 $ MeV/c and$ Q_4 = 30 $ MeV/c, respectively, for partially coherent pion emissions from a droplet with$ p' = 0.5 $ GeV/c,$ p' = 0.7 $ GeV/c, and$ p' = \infty $ . One can see that the intercept results are almost within the error range.$p'$ /(GeV/c)

0.5 0.7 $\infty$ 

$r_3(Q_3\!=\!10$ MeV/c)

$0.16\!<\!\!K_{T3}\!\!<\!0.3\,{\rm{GeV/c}}\!$ 

$1.64\pm0.13$ 

$1.51\pm0.10$ 

$1.47\pm0.11$ 

$0.3\!<\!K_{T3}\!<\!1\,{\rm{GeV/c}}\!$ 

$1.67\pm0.14$ 

$1.54\pm0.10$ 

$1.45\pm0.12$ 

$r_4(Q_4\!=\!30$ MeV/c)

$0.16\!<\!\!K_{T4}\!\!<\!0.3\,{\rm{GeV/c}}\!$ 

$2.45\pm0.21$ 

$2.29\pm0.18$ 

$2.14\pm0.12$ 

$0.3\!<\!K_{T4}\!<\!1\,{\rm{GeV/c}}\!$ 

$2.07\pm0.24$ 

$2.15\pm0.22$ 

$1.98\pm0.19$ 

Table 1. Results for
$r_3(Q_3\!=\!10$ MeV/c) and$r_4(Q_4\!=\!30$ MeV/c), for partially coherent pion emissions from a droplet with$p'\!=\!0.5$ GeV/c,$p'\!=\!0.7$ GeV/c, and$p'\!=\!\infty$ . -
We studied three- and four-pion BECs in the granular source model with coherent pion-emission droplets. The three- and four-pion correlation functions and the normalized multi-pion correlation functions of granular sources were examined for completely coherent and momentum-dependent partially coherent pion-emissions from one droplet. It was found that the intercepts of the multi-pion correlation functions at the relative momenta near zero were sensitive to the number of droplets in the granular source, decreasing with the number of droplets.
By comparing the three- and four-pion correlation functions of evolving granular sources with the experimental data for Pb-Pb collisions at
$ \sqrt{s_{NN}} = 2.76 $ TeV at the LHC, we found that the three-pion correlation functions of evolving granular sources with momentum-dependent partially coherent pion-emission droplets were in a basic agreement with the experimental results for the transverse-momentum intervals$ 0.16<K_{T3}<0.3 $ GeV/c and$ 0.3< $ $ K_{T3}<1 $ GeV/c. However, the model results for the four-pion correlation function were inconsistent with the experimental data. To solve the puzzle of the multi-pion correlation functions, more consideration should be given to coherent pion emission. For instance, coherent emission may depend not only on the magnitude of the particle momentum but also on its azimuthal angle. Figures 5(c) and 5(d) show that the model results for the higher-transverse-momentum$ K_{T4} $ interval have more enhancements compared with the experimental data, than those for the lower-transverse-momentum$ K_{T4} $ intervals. This may indicate that pions with small relative azimuthal angles (and thus larger$ K_{T4} $ ) possibly exhibit coherent emission, although their momenta are above$ p' $ . The four-particle correlations are sensitive to coherent emission and should be studied in more detail in model and experimental data analyses.The normalized multi-pion correlation functions, defined as the ratios of the multi-pion cumulant correlators to the two-pion correlator, can reduce the influence of the resonance decay on themselves. Our investigations indicate that the normalized four-pion correlation function is improved in the
$ Q_4\sim\!100 $ -MeV/c region for the wide transverse momentum interval$ 0.3<K_{T4}<1 $ GeV/c. This can be attributed to the notion that high-momentum pions are more likely emitted chaotically from excited states.Recently, D. Gangadharan proposed a technique for constructing three- and four-pion correlation functions for partially coherent sources and for estimating the source coherence [9]. Using this technique, the ALICE Collaboration analyzed the three- and four-pion correlation functions for Pb-Pb collisions at
$ \sqrt{s_{NN}} = 2.76 $ TeV at the LHC [8]. They found that the source coherent fraction extracted from the four-pion correlation function cannot explain the three-pion correlation function if the sources are assumed partially coherent [8]. How to consistently solve the suppressions of the three- and four-pion BECs in a partially coherent source model is an open question.Finally, it should be mentioned that the granular source model used in this paper had the same model parameters as in Ref. [46], but with the assumption of coherent pion emission from one droplet. We noted that this assumption may increase the two-pion interferometry radii by
$ \sim 4 $ % on average and decrease the two-pion chaoticity parameter$ \lambda $ by$ \sim 10 $ %. However, the assumption of coherent pion emission hardly changes the results for the transverse-momentum spectrum and elliptic flow. Considering more realistic pion coherent emissions, applying Gangadharan's technique to granular sources, and investigating multi-pion BECs in a more realistic model will be of interest. -
With the formulism developed in Refs. [51, 52], one can develop the four-pion correlation function of a static granular source with completely chaotic pion emission droplets as
$ \begin{aligned}[b] C_4({{p}}_1,{{p}}_2,{{p}}_3,{{p}}_4) =& 1+\frac{1}{n}\bigg[{\rm e}^{-{{q}}_{12}^2 r_d^2} +{\rm e}^{-{{q}}_{13}^2 r_d^2}+{\rm e}^{-{{q}}_{14}^2 r_d^2}+{\rm e}^{-{{q}}_{23}^2 r_d^2}+{\rm e}^{-{{q}}_{24}^2 r_d^2} +{\rm e}^{-{{q}}_{34}^2 r_d^2}\bigg] +\frac{(n\!-\!1)}{n}\bigg[{\rm e}^{-{{q}}_{12}^2 (r_d^2+R_G^2)}\\ &+\,{\rm e}^{-{{q}}_{13}^2 (r_d^2+R_G^2)} +{\rm e}^{-{{q}}_{14}^2 (r_d^2+R_G^2)}+{\rm e}^{-{{q}}_{23}^2 (r_d^2+R_G^2)} +{\rm e}^{-{{q}}_{24}^2 (r_d^2+R_G^2)} +{\rm e}^{-{{q}}_{34}^2 (r_d^2+R_G^2)} \bigg]\\ &+\,\frac{2}{n^2}\bigg[{\rm e}^{\!-\!({{q}}_{12}^2+{{q}}_{13}^2+{{q}}_{23}^2)r_d^2/2} \!+\!{\rm e}^{\!-\!({{q}}_{12}^2+{{q}}_{14}^2+{{q}}_{24}^2)r_d^2/2}\!+\!{\rm e}^{\!-\!({{q}}_{13}^2 +{{q}}_{14}^2+{{q}}_{34}^2)r_d^2/2}\!+\!{\rm e}^{\!-\!({{q}}_{23}^2+{{q}}_{24}^2+{{q}}_{34}^2)r_d^2/2} \bigg] \\ &+\frac{2(n-1)(n-2)}{n^2}\bigg[{\rm e}^{-({{q}}_{12}^2+{{q}}_{13}^2+{{q}}_{23}^2)(r_d^2+R_G^2)/2} +{\rm e}^{-({{q}}_{12}^2+{{q}}_{14}^2+{{q}}_{24}^2)(r_d^2+R_G^2)/2} \\ &+\,{\rm e}^{-({{q}}_{13}^2+{{q}}_{14}^2+{{q}}_{34}^2)(r_d^2+R_G^2)/2} +{\rm e}^{-({{q}}_{23}^2+{{q}}_{24}^2+{{q}}_{34}^2)(r_d^2+R_G^2)/2} \bigg] \\ &+\frac{2(n-1)}{n^2}\bigg[{\rm e}^{-({{q}}_{12}^2+{{q}}_{13}^2+{{q}}_{23}^2)r_d^2/2} \Big( {\rm e}^{\!-\!{{q}}_{12}^2R_G^2}\!+\!{\rm e}^{\!-\!{{q}}_{13}^2R_G^2}\!+\!{\rm e}^{\!-\!{{q}}_{23}^2R_G^2} \Big) +{\rm e}^{-({{q}}_{12}^2+{{q}}_{14}^2+{{q}}_{24}^2)r_d^2/2}\\ &\times\,\Big({\rm e}^{\!-\!{{q}}_{12}^2 R_G^2} \!+\!{\rm e}^{\!-\!{{q}}_{14}^2R_G^2} \!+\!{\rm e}^{\!-\!{{q}}_{24}^2 R_G^2}\Big) \!+\!{\rm e}^{\!-\!({{q}}_{13}^2+{{q}}_{14}^2 +{{q}}_{34}^2)r_d^2/2}\Big({\rm e}^{\!-\!{{q}}_{13}^2 R_G^2}+{\rm e}^{\!-\!{{q}}_{14}^2 R_G^2}\!+\!{\rm e}^{\!-\!{{q}}_{34}^2 R_G^2}\Big) \\ &+{\rm e}^{-({{q}}_{23}^2+{{q}}_{24}^2+{{q}}_{34}^2)r_d^2/2}\Big({\rm e}^{-{{q}}_{23}^2 R_G^2} +{\rm e}^{-{{q}}_{24}^2 R_G^2}+{\rm e}^{-{{q}}_{34}^2 R_G^2}\Big)\bigg] +\frac{1}{n^2}\bigg[{\rm e}^{-({{q}}_{12}^2+{{q}}_{34}^2)r_d^2} \\ &+\,{\rm e}^{-({{q}}_{13}^2+{{q}}_{24}^2)r_d^2} +{\rm e}^{-({{q}}_{14}^2+{{q}}_{23}^2)r_d^2} \bigg] +\frac{(n-1)(n-2)(n-3)}{n^3}\bigg[{\rm e}^{-({{q}}_{12}^2+{{q}}_{34}^2)(r_d^2+R_G^2)} \\ & +\,{\rm e}^{-({{q}}_{13}^2+{{q}}_{24}^2)(r_d^2+R_G^2)} +{\rm e}^{-({{q}}_{14}^2 +{{q}}_{23}^2)(r_d^2+R_G^2)} \bigg] +\frac{(n-1)}{n^2}\bigg[{\rm e}^{-{{q}}_{12}^2 r_d^2} {\rm e}^{-{{q}}_{34}^2 (r_d^2+R_G^2)}\\ & +\,{\rm e}^{\!-\!{{q}}_{13}^2 r_d^2} {\rm e}^{\!-\!{{q}}_{24}^2 (r_d^2+\!R_G^2)}\!+\!{\rm e}^{\!-\!{{q}}_{14}^2 r_d^2} {\rm e}^{\!-\!{{q}}_{23}^2 (r_d^2+\!R_G^2)} \!+\!{\rm e}^{\!-\!{{q}}_{23}^2 r_d^2} {\rm e}^{\!-\!{{q}}_{14}^2(r_d^2+\!R_G^2)} \!+\!{\rm e}^{\!-\!{{q}}_{24}^2 r_d^2} {\rm e}^{\!-\!{{q}}_{13}^2(r_d^2+\!R_G^2)} \\ & +\,{\rm e}^{\!-{{q}}_{34}^2r_d^2}{\rm e}^{\!-{{q}}_{12}^2(r_d^2+R_G^2)} \bigg] +\frac{(n-1)}{n^3}\bigg[{\rm e}^{-({{q}}_{12}^2+{{q}}_{34}^2)r_d^2} {\rm e}^{-({{q}}_{12} +{{q}}_{34})^2 R_G^2} +{\rm e}^{-({{q}}_{12}^2+{{q}}_{34}^2)r_d^2} \\ &\times\,{\rm e}^{-({{q}}_{12} +{{q}}_{43})^2 R_G^2} +{\rm e}^{-({{q}}_{13}^2+{{q}}_{24}^2)r_d^2} {\rm e}^{\!-({{q}}_{13}+{{q}}_{24})^2 R_G^2} +{\rm e}^{\!-({{q}}_{13}^2+{{q}}_{24}^2)r_d^2} {\rm e}^{\!-({{q}}_{13}+{{q}}_{42})^2 R_G^2} \\ &+\,{\rm e}^{\!-({{q}}_{14}^2+{{q}}_{23}^2)r_d^2} {\rm e}^{\!-({{q}}_{14}+{{q}}_{23})^2 R_G^2} +{\rm e}^{\!-({{q}}_{14}^2+{{q}}_{23}^2)r_d^2} {\rm e}^{\!-({{q}}_{14}+{{q}}_{32})^2 R_G^2}\bigg] \\ &+\,\frac{2(n-1)(n-2)}{n^3}\bigg[{\rm e}^{-({{q}}_{12}^2+{{q}}_{34}^2)r_d^2} {\rm e}^{-({{q}}_{12}^2 +{{q}}_{34}^2) R_G^2/2} \Big({\rm e}^{-({{q}}_{12}+{{q}}_{34})^2 R_G^2/2} +{\rm e}^{-({{q}}_{12}+ {{q}}_{43})^2 R_G^2/2}\Big) \\ &+\,{\rm e}^{-({{q}}_{13}^2+{{q}}_{24}^2)r_d^2}{\rm e}^{-({{q}}_{13}^2+{{q}}_{24}^2)R_G^2/2} \Big( {\rm e}^{-({{q}}_{13}+{{q}}_{24})^2R_G^2/2}+{\rm e}^{-({{q}}_{13}+{{q}}_{42})^2R_G^2/2} \Big) \\ & +\,{\rm e}^{-({{q}}_{14}^2+{{q}}_{23}^2)r_d^2} {\rm e}^{-({{q}}_{14}^2+{{q}}_{23}^2)R_G^2/2} \Big( {\rm e}^{-({{q}}_{14}+{{q}}_{23})^2R_G^2/2}+{\rm e}^{-({{q}}_{14}+{{q}}_{32})^2R_G^2/2} \Big) \bigg] \\ & +\,\frac{2}{n^3}\bigg[{\rm e}^{-({{q}}_{12}^2+{{q}}_{23}^2+{{q}}_{34}^2+{{q}}_{41}^2)r_d^2/2} +{\rm e}^{-({{q}}_{12}^2+{{q}}_{24}^2+{{q}}_{43}^2+{{q}}_{31}^2)r_d^2/2} +{\rm e}^{-({{q}}_{13}^2+{{q}}_{32}^2+{{q}}_{24}^2+{{q}}_{41}^2)r_d^2/2}\bigg] \\ &+\,\frac{2(n\!-\!1)(n\!-\!2)(n\!-\!3)}{n^3}\bigg[{\rm e}^{\!-\!({{q}}_{12}^2+{{q}}_{23}^2 +{{q}}_{34}^2+{{q}}_{41}^2)(r_d^2+\!R_G^2)/2} +{\rm e}^{\!-\!({{q}}_{12}^2+{{q}}_{24}^2 +{{q}}_{43}^2+{{q}}_{31}^2)(r_d^2+\!R_G^2)/2} \\ &+\,{\rm e}^{-({{q}}_{13}^2+{{q}}_{32}^2+{{q}}_{24}^2+{{q}}_{41}^2)(r_d^2+\!R_G^2)/2}\bigg] +\frac{2(n\!-\!1)}{n^3}\bigg[{\rm e}^{-({ q}_{12}^2+{ q}_{23}^2+{ q}_{34}^2+{ q}_{41}^2)r_d^2/2}\Big({\rm e}^{-{ q}_{12}^{2}R_{G}^{2}} \\ & +\,{\rm e}^{-{{q}}_{23}^2R_G^2}\!+\!e^{-{{q}}_{34}^2R_G^2}+{\rm e}^{-{{q}}_{41}^2R_G^2}\Big) \!+\!{\rm e}^{-({{q}}_{12}^2+{{q}}_{24}^2+{{q}}_{43}^2\!+\!{{q}}_{31}^2)r_d^2/2}\Big({\rm e}^{-{{q}}_{12}^2 R_G^2}\!+\!{\rm e}^{-{{q}}_{24}^2R_G^2} \\ & +\,{\rm e}^{\!-\!{{q}}_{43}^2R_G^2}\!+\!{\rm e}^{\!-\!{{q}}_{31}^2R_G^2}\Big)\!+\!{\rm e}^{\!-\!({{q}}_{13}^2 +{{q}}_{32}^2+{{q}}_{24}^2+{{q}}_{41}^2)r_d^2/2} \Big({\rm e}^{\!-\!{{q}}_{13}^2R_G^2} \!+\!{\rm e}^{\!-\!{{q}}_{32}^2R_G^2}\!+\!{\rm e}^{\!-\!{{q}}_{24}^2R_G^2}\!+\!{\rm e}^{\!-\!{{q}}_{41}^2R_G^2} \Big)\bigg] \\ &+\,\frac{(n-1)}{n^3}\bigg[{\rm e}^{-({{q}}_{12}^2+{{q}}_{23}^2+{{q}}_{34}^2+{{q}}_{41}^2)r_d^2/2} \Big({\rm e}^{-({{q}}_{12}+{{q}}_{23})^2R_G^2}+{\rm e}^{-({{q}}_{12}+{{q}}_{34})^2R_G^2} +{\rm e}^{-({\bf{q}}_{12}+{\bf{q}}_{41})^2R_G^2} \\ &+\,{\rm e}^{-({{q}}_{23}+{{q}}_{34})^2R_G^2}+{\rm e}^{-({{q}}_{23}+{{q}}_{41})^2R_G^2} +{\rm e}^{-({{q}}_{34}+{{q}}_{41})^2R_G^2}\Big) +{\rm e}^{-({{q}}_{12}^2+{{q}}_{24}^2+{{q}}_{43}^2+{{q}}_{31}^2)r_d^2/2} \\ &\times\,\Big({\rm e}^{\!-\!({{q}}_{12}+{{q}}_{24})^2\!R_G^2}\!+\!{\rm e}^{\!-\!({{q}}_{12}+{{q}}_{43})^2 \!R_G^2}\!+\!{\rm e}^{\!-\!({{q}}_{12}+{{q}}_{31})^2\!R_G^2}\!+\!{\rm e}^{\!-\!({{q}}_{24}+{{q}}_{43})^2 \!R_G^2}\!+\!{\rm e}^{\!-\!({{q}}_{24}+{{q}}_{31})^2\!R_G^2} \\ &+\,{\rm e}^{-({{q}}_{43}+{{q}}_{31})^2R_G^2}\Big) +{\rm e}^{-({{q}}_{13}^2+{{q}}_{32}^2+{{q}}_{24}^2 +{{q}}_{41}^2)r_d^2/2} \Big({\rm e}^{-({{q}}_{13}+{{q}}_{32})^2R_G^2}+{\rm e}^{-({{q}}_{13}+{{q}}_{24})^2 R_G^2} \\ &+{\rm e}^{-({{q}}_{13}+{{q}}_{41})^2R_G^2}+{\rm e}^{-({{q}}_{32}+{{q}}_{24})^2R_G^2} +{\rm e}^{-({{q}}_{32}+{{q}}_{41})^2R_G^2}+{\rm e}^{-({{q}}_{24}+{{q}}_{41})^2R_G^2} \Big) \bigg] \\ &+\,\frac{2(n-1)(n-2)}{n^3}\bigg[{\rm e}^{-({{q}}_{12}^2+{{q}}_{23}^2+{{q}}_{34}^2+{{q}}_{41}^2) r_d^2/2} \Big({\rm e}^{-({{q}}_{12}^2+{{q}}_{13}^2+{{q}}_{23}^2)R_G^2/2} \!+\!\,{\rm e}^{-({{q}}_{12}^2 +{{q}}_{14}^2+{{q}}_{24}^2)R_G^2/2} \\ & +\,{\rm e}^{-({{q}}_{13}^2 +{{q}}_{14}^2+{{q}}_{34}^2)R_G^2/2} +{\rm e}^{-({{q}}_{23}^2 +{{q}}_{24}^2+{{q}}_{34}^2)R_G^2/2} +{\rm e}^{-({{q}}_{12}^2+{{q}}_{34}^2)R_G^2/2} {\rm e}^{-({{q}}_{12}+{{q}}_{43})^2R_G^2/2} \\ \end{aligned} $

$ \tag{A1} \begin{aligned}[b] &+\,{\rm e}^{-({{q}}_{14}^2+{{q}}_{23}^2)R_G^2/2} {\rm e}^{-({{q}}_{14}+{{q}}_{32})^2R_G^2/2}\Big) \!+\!{\rm e}^{-({{q}}_{12}^2+{{q}}_{24}^2+{{q}}_{43}^2+{{q}}_{31}^2)r_d^2/2} \Big( {\rm e}^{-({{q}}_{12}^2+{{q}}_{13}^2+{\bf{q}}_{23}^2)R_G^2/2} \\ &+\,{\rm e}^{-({{q}}_{12}^2 +{{q}}_{14}^2+{{q}}_{24}^2)R_G^2/2} +{\rm e}^{-({{q}}_{13}^2 +{{q}}_{14}^2+{{q}}_{34}^2)R_G^2/2} +{\rm e}^{-({{q}}_{23}^2 +{{q}}_{24}^2+{{q}}_{24}^2)R_G^2/2} \\ &+\,{\rm e}^{-({{q}}_{13}^2+{{q}}_{24}^2)R_G^2/2} {\rm e}^{-({{q}}_{13}+{{q}}_{42})^2R_G^2/2} +{\rm e}^{-({{q}}_{12}^2+{{q}}_{34}^2)R_G^2/2} {\rm e}^{-({{q}}_{12}+{{q}}_{43})^2R_G^2/2}\Big) \\ & +\,{\rm e}^{-({{q}}_{13}^2 +{{q}}_{32}^2+{{q}}_{24}^2+{{q}}_{41}^2)r_d^2/2} \Big({\rm e}^{-({{q}}_{12}^2+{{q}}_{13}^2+{{q}}_{23}^2)R_G^2/2} +{\rm e}^{-({{q}}_{12}^2 +{{q}}_{14}^2+{{q}}_{24}^2)R_G^2/2} \\ &+\,{\rm e}^{-({{q}}_{13}^2 +{{q}}_{14}^2+{{q}}_{34}^2)R_G^2/2} +{\rm e}^{-({{q}}_{23}^2 +{{q}}_{24}^2+{{q}}_{34}^2)R_G^2/2} +{\rm e}^{-({{q}}_{13}^2+{{q}}_{24}^2)R_G^2/2} {\rm e}^{-({{q}}_{13}+{{q}}_{42})^2R_G^2/2} +\,{\rm e}^{-({{q}}_{14}^2+{{q}}_{23}^2)R_G^2/2} {\rm e}^{-({{q}}_{14}+{{q}}_{32})^2R_G^2/2}\Big)\bigg], \end{aligned} $

where
$ {{q}}_{ij} = {{p}}_i-{{p}}_j\; (i,j = 1,2,3,4) $ , and n is the droplet number in the granular source. In Eq. (A1), the first and second pairs of square brackets express the correlations of two pions that are emitted from one droplet and from two different droplets, respectively; the third and forth pairs of square brackets express the pure triplet correlations of three pions that are emitted from one droplet and from three different droplets, respectively; the fifth pair of square brackets expresses the pure triplet correlations of three pions where two pions are emitted from one droplet and another pion is emitted from a different droplet; the sixth and seventh pairs of square brackets express the correlations of double pion pairs where each pair is emitted from one droplet and the four pions are emitted from four different droplets, respectively; the eighth pair of square brackets expresses the correlations of double pion pairs where one pion pair is emitted from one droplet and the two pions of another pair are emitted from two different droplets; the ninth pair of square brackets expresses the correlations of double pion pairs where the two pions of a pair are emitted from two different droplets and the two pions of another pair are emitted respectively from the two droplets as well; the tenth pair of square brackets expresses the correlations of double pion pairs where the two pions of a pair are emitted from two different droplets and the two pions of another pair are emitted respectively from one of the same droplets and from another droplet; the eleventh and twelfth pairs of square brackets express the pure quadruplet correlations of four pions emitted from one droplet and from four different droplets, respectively; the thirteenth pair of square brackets expresses the pure quadruplet correlations of four pions where three pions are emitted from one droplet and another pion is emitted from a different droplet; the fourteenth pair of square brackets expresses the pure quadruplet correlations of four pions where two pions are emitted from one droplet and the other two pions are emitted from another droplet; and finally, the fifteenth pair of square brackets expresses the pure quadruplet correlations of four pions where two pions are emitted from one droplet and the other two pions are respectively emitted from two different droplets.The four-pion correlation function of a granular source is complex, including the relative angles of two relative momenta in the double pair correlations and pure quadruplet correlations. For a completely chaotic pion emission droplet,
$ C_4({{p}}_1,{{p}}_2,{{p}}_3,{{p}}_4) = 24 $ when$ {{q}}_{ij} = 0 $ $(i,j = 1,2,3,4) $ . For a partially coherent pion-emission from a droplet, if the coherent emission in a droplet has the same Gaussian distribution of the chaotic pion emission and a constant ratio of the coherent emission contribution$ b_c $ to the chaotic emission contribution$ b_\chi $ ,$ \gamma = b_c/b_\chi $ , the terms of two, pure triplet, double pair, and pure quadruplet pion correlations are reduced by the factors [12, 56]$ \lambda = (1+2\gamma) /(1+\gamma)^2 $ ,$ \xi = (1+3\gamma)/(1+\gamma)^3 $ ,$ \lambda^2 $ , and$ \eta = (1+4\gamma) /(1+\gamma)^4 $ , respectively. In this case, the four-pion correlation function of a granular source with partially coherent pion-emission droplets is given by,$ \begin{aligned}[b] C_4({{p}}_1,{{p}}_2,{{p}}_3,{{p}}_4) =& 1+\frac{\lambda}{n}\bigg[{\rm e}^{-{{q}}_{12}^2 r_d^2} +{\rm e}^{-{{q}}_{13}^2r_d^2}+{\rm e}^{-{{q}}_{14}^2 r_d^2}+{\rm e}^{-{{q}}_{23}^2 r_d^2} +{\rm e}^{-{{q}}_{24}^2 r_d^2} +{\rm e}^{-{{q}}_{34}^2r_d^2}\bigg] +\frac{(n\!-\!1)}{n}\bigg[{\rm e}^{-{{q}}_{12}^2 (r_d^2+R_G^2)} \\ &+\,{\rm e}^{-{{q}}_{13}^2 (r_d^2+R_G^2)} +{\rm e}^{-{{q}}_{14}^2 (r_d^2+R_G^2)}+{\rm e}^{-{{q}}_{23}^2 (r_d^2+R_G^2)} +{\rm e}^{-{{q}}_{24}^2 (r_d^2+R_G^2)} +{\rm e}^{-{{q}}_{34}^2 (r_d^2+R_G^2)}\bigg] \\ &+\,\frac{2\xi}{n^2}\bigg[{\rm e}^{\!-\!({{q}}_{12}^2+{{q}}_{13}^2+{{q}}_{23}^2)r_d^2/2} \!+\!{\rm e}^{\!-\!({{q}}_{12}^2+{{q}}_{14}^2+{{q}}_{24}^2)r_d^2/2}\!+\!{\rm e}^{\!-\!({{q}}_{13}^2 +{{q}}_{14}^2+{{q}}_{34}^2)r_d^2/2}\!+\!{\rm e}^{\!-\!({{q}}_{23}^2+{{q}}_{24}^2+{{q}}_{34}^2)r_d^2/2} \bigg] \\& +\frac{2(n-1)(n-2)}{n^2}\bigg[{\rm e}^{-({{q}}_{12}^2+{{q}}_{13}^2+{{q}}_{23}^2)(r_d^2+R_G^2)/2} +{\rm e}^{-({{q}}_{12}^2+{{q}}_{14}^2+{{q}}_{24}^2)(r_d^2+R_G^2)/2} \\ &+\,{\rm e}^{-({{q}}_{13}^2+{{q}}_{14}^2+{{q}}_{34}^2)(r_d^2+R_G^2)/2} +{\rm e}^{-({{q}}_{23}^2+{{q}}_{24}^2+{{q}}_{34}^2)(r_d^2+R_G^2)/2} \bigg] \\ &+\frac{2(n-1)\lambda}{n^2}\bigg[{\rm e}^{-({{q}}_{12}^2+{{q}}_{13}^2+{{q}}_{23}^2)r_d^2/2} \Big( {\rm e}^{\!-\!{{q}}_{12}^2R_G^2}\!+\!{\rm e}^{\!-\!{{q}}_{13}^2R_G^2}\!+\!{\rm e}^{\!-\!{{q}}_{23}^2R_G^2} \Big) +{\rm e}^{-({{q}}_{12}^2+{{q}}_{14}^2+{{q}}_{24}^2)r_d^2/2} \\&\times\,\Big({\rm e}^{\!-\!{{q}}_{12}^2 R_G^2} \!+\!{\rm e}^{\!-\!{{q}}_{14}^2R_G^2} \!+\!{\rm e}^{\!-\!{{q}}_{24}^2 R_G^2}\Big) \!+\!{\rm e}^{\!-\!({{q}}_{13}^2+{{q}}_{14}^2 +{{q}}_{34}^2)r_d^2/2}\Big({\rm e}^{\!-\!{{q}}_{13}^2 R_G^2}+{\rm e}^{\!-\!{{q}}_{14}^2 R_G^2}\!+\!{\rm e}^{\!-\!{{q}}_{34}^2 R_G^2}\Big) \end{aligned} $

$ \tag{A2} \begin{aligned}[b] & +{\rm e}^{-({{q}}_{23}^2+{{q}}_{24}^2+{{q}}_{34}^2)r_d^2/2}\Big({\rm e}^{-{{q}}_{23}^2 R_G^2} +{\rm e}^{-{{q}}_{24}^2 R_G^2}+{\rm e}^{-{{q}}_{34}^2 R_G^2}\Big)\bigg]+\frac{\lambda^2}{n^2}\bigg[{\rm e}^{-({{q}}_{12}^2+{{q}}_{34}^2)r_d^2} \\ & +\,{\rm e}^{-({{q}}_{13}^2+{{q}}_{24}^2)r_d^2} +{\rm e}^{-({{q}}_{14}^2+{{q}}_{23}^2)r_d^2} \bigg] +\frac{(n-1)(n-2)(n-3)}{n^3}\bigg[{\rm e}^{-({{q}}_{12}^2+{{q}}_{34}^2)(r_d^2+R_G^2)} \\&+\,{\rm e}^{-({{q}}_{13}^2+{{q}}_{24}^2)(r_d^2+R_G^2)} +{\rm e}^{-({{q}}_{14}^2 +{{q}}_{23}^2)(r_d^2+R_G^2)} \bigg] +\frac{(n-1)\lambda}{n^2}\bigg[{\rm e}^{-{{q}}_{12}^2 r_d^2} e^{-{{q}}_{34}^2 (r_d^2+R_G^2)} \\ &+\,{\rm e}^{\!-\!{{q}}_{13}^2 r_d^2} {\rm e}^{\!-\!{{q}}_{24}^2 (r_d^2+\!R_G^2)}\!+\!{\rm e}^{\!-\!{{q}}_{14}^2 r_d^2} {\rm e}^{\!-\!{{q}}_{23}^2 (r_d^2+\!R_G^2)} \!+\!{\rm e}^{\!-\!{{q}}_{23}^2 r_d^2} {\rm e}^{\!-\!{{q}}_{14}^2(r_d^2+\!R_G^2)} \!+\!{\rm e}^{\!-\!{{q}}_{24}^2 r_d^2} {\rm e}^{\!-\!{{q}}_{13}^2(r_d^2+\!R_G^2)} \\ & +\,{\rm e}^{\!-{{q}}_{34}^2r_d^2}{\rm e}^{\!-{{q}}_{12}^2(r_d^2+R_G^2)} \bigg] +\frac{(n-1)}{n^3}\bigg[{\rm e}^{-({{q}}_{12}^2+{{q}}_{34}^2)r_d^2} {\rm e}^{-({{q}}_{12} +{{q}}_{34})^2 R_G^2} +{\rm e}^{-({{q}}_{12}^2+{{q}}_{34}^2)r_d^2} \\ & \times\,{\rm e}^{-({{q}}_{12}+{{q}}_{43})^2 R_G^2} +{\rm e}^{-({{q}}_{13}^2+{{q}}_{24}^2)r_d^2} {\rm e}^{\!-({{q}}_{13}+{{q}}_{24})^2 R_G^2} +{\rm e}^{\!-({{q}}_{13}^2+{{q}}_{24}^2)r_d^2} {\rm e}^{\!-({{q}}_{13}+{{q}}_{42})^2 R_G^2} \\ &+\,{\rm e}^{\!-({{q}}_{14}^2+{{q}}_{23}^2)r_d^2} {\rm e}^{\!-({{q}}_{14}+{{q}}_{23})^2 R_G^2} +{\rm e}^{\!-({{q}}_{14}^2+{{q}}_{23}^2)r_d^2} {\rm e}^{\!-({{q}}_{14}+{{q}}_{32})^2 R_G^2}\bigg] \\ & +\,\frac{2(n-1)(n-2)}{n^3}\bigg[{\rm e}^{-({{q}}_{12}^2+{{q}}_{34}^2)r_d^2} {\rm e}^{-({{q}}_{12}^2 +{{q}}_{34}^2) R_G^2/2} \Big({\rm e}^{-({{q}}_{12}+{{q}}_{34})^2 R_G^2/2} +{\rm e}^{-({{q}}_{12}+ {{q}}_{43})^2 R_G^2/2}\Big) \\ & +\,{\rm e}^{-({{q}}_{13}^2+{{q}}_{24}^2)r_d^2}{\rm e}^{-({{q}}_{13}^2+{{q}}_{24}^2)R_G^2/2} \Big( {\rm e}^{-({{q}}_{13}+{{q}}_{24})^2R_G^2/2}+{\rm e}^{-({{q}}_{13}+{{q}}_{42})^2R_G^2/2} \Big) \\& +\,{\rm e}^{-({{q}}_{14}^2+{{q}}_{23}^2)r_d^2} {\rm e}^{-({{q}}_{14}^2+{{q}}_{23}^2)R_G^2/2} \Big( {\rm e}^{-({{q}}_{14}+{{q}}_{23})^2R_G^2/2}+{\rm e}^{-({{q}}_{14}+{{q}}_{32})^2R_G^2/2} \Big) \bigg] \\ & +\,\frac{2\eta}{n^3}\bigg[{\rm e}^{-({{q}}_{12}^2+{{q}}_{23}^2+{{q}}_{34}^2+{{q}}_{41}^2)r_d^2/2} +{\rm e}^{-({{q}}_{12}^2+{{q}}_{24}^2+{{q}}_{43}^2+{{q}}_{31}^2)r_d^2/2} +{\rm e}^{-({{q}}_{13}^2+{{q}}_{32}^2+{{q}}_{24}^2+{{q}}_{41}^2)r_d^2/2}\bigg] \\ &+\,\frac{2(n\!-\!1)(n\!-\!2)(n\!-\!3)}{n^3}\bigg[{\rm e}^{\!-\!({{q}}_{12}^2+{{q}}_{23}^2 +{{q}}_{34}^2+{{q}}_{41}^2)(r_d^2+\!R_G^2)/2} +{\rm e}^{\!-\!({{q}}_{12}^2+{{q}}_{24}^2 +{{q}}_{43}^2+{{q}}_{31}^2)(r_d^2+\!R_G^2)/2} \\ &+\,{\rm e}^{\!-\!({{q}}_{13}^2+{{q}}_{32}^2+{{q}}_{24}^2+{{q}}_{41}^2)(r_d^2+\!R_G^2)/2}\bigg] +\frac{2(n\!-\!1)\xi}{n^3}\bigg[{\rm e}^{\!-\!({{q}}_{12}^2+{{q}}_{23}^2+{{q}}_{34}^2+{{q}}_{41}^2) r_d^2/2}\Big({\rm e}^{-{{q}}_{12}^2R_G^2} \\ & +\,{\rm e}^{-{{q}}_{23}^2R_G^2}\!+\!{\rm e}^{-{{q}}_{34}^2R_G^2}+{\rm e}^{-{{q}}_{41}^2R_G^2}\Big) \!+\!{\rm e}^{-({{q}}_{12}^2+{{q}}_{24}^2+{{q}}_{43}^2\!+\!{{q}}_{31}^2)r_d^2/2}\Big({\rm e}^{-{{q}}_{12}^2 R_G^2}\!+\!{\rm e}^{-{{q}}_{24}^2R_G^2} \\ &+\,{\rm e}^{\!-\!{{q}}_{43}^2R_G^2}\!+\!{\rm e}^{\!-\!{{q}}_{31}^2R_G^2}\Big)\!+\!{\rm e}^{\!-\!({{q}}_{13}^2 +{{q}}_{32}^2+{{q}}_{24}^2+{{q}}_{41}^2)r_d^2/2} \Big({\rm e}^{\!-\!{{q}}_{13}^2R_G^2} \!+\!{\rm e}^{\!-\!{{q}}_{32}^2R_G^2}\!+\!{\rm e}^{\!-\!{{q}}_{24}^2R_G^2}\!+\!{\rm e}^{\!-\!{{q}}_{41}^2R_G^2} \Big)\bigg] \\ &+\,\frac{(n-1)\lambda^2}{n^3}\bigg[{\rm e}^{-({{q}}_{12}^2+{{q}}_{23}^2+{{q}}_{34}^2+{{q}}_{41}^2) r_d^2/2} \Big({\rm e}^{-({{q}}_{12}+{{q}}_{23})^2R_G^2}+{\rm e}^{-({{q}}_{12}+{{q}}_{34})^2R_G^2} +{\rm e}^{-({{q}}_{12}+{{q}}_{41})^2R_G^2} \\& +\,{\rm e}^{-({{q}}_{23}+{{q}}_{34})^2R_G^2}+{\rm e}^{-({{q}}_{23}+{{q}}_{41})^2R_G^2} +{\rm e}^{-({{q}}_{34}+{{q}}_{41})^2R_G^2}\Big) +{\rm e}^{-({{q}}_{12}^2+{{q}}_{24}^2+{{q}}_{43}^2+{{q}}_{31}^2)r_d^2/2} \\ & \times\,\Big({\rm e}^{\!-\!({{q}}_{12}+{{q}}_{24})^2\!R_G^2}\!+\!{\rm e}^{\!-\!({{q}}_{12}+{{q}}_{43})^2 \!R_G^2}\!+\!{\rm e}^{\!-\!({{q}}_{12}+{{q}}_{31})^2\!R_G^2}\!+\!{\rm e}^{\!-\!({{q}}_{24}+{{q}}_{43})^2 \!R_G^2}\!+\!{\rm e}^{\!-\!({{q}}_{24}+{{q}}_{31})^2\!R_G^2} \\ & +\,{\rm e}^{-({{q}}_{43}+{{q}}_{31})^2R_G^2}\Big) +{\rm e}^{-({{q}}_{13}^2+{{q}}_{32}^2+{{q}}_{24}^2 +{{q}}_{41}^2)r_d^2/2} \Big({\rm e}^{-({{q}}_{13}+{{q}}_{32})^2R_G^2}+{\rm e}^{-({{q}}_{13}+{{q}}_{24})^2 R_G^2} \\& +{\rm e}^{-({{q}}_{13}+{{q}}_{41})^2R_G^2}+{\rm e}^{-({{q}}_{32}+{{q}}_{24})^2R_G^2} +{\rm e}^{-({{q}}_{32}+{{q}}_{41})^2R_G^2}+{\rm e}^{-({{q}}_{24}+{{q}}_{41})^2R_G^2} \Big) \bigg] \\ &+\,\frac{2(n-1)(n-2)\lambda}{n^3}\bigg[{\rm e}^{-({{q}}_{12}^2+{{q}}_{23}^2+{{q}}_{34}^2 +{{q}}_{41}^2)r_d^2/2} \Big({\rm e}^{-({{q}}_{12}^2+{{q}}_{13}^2+{{q}}_{23}^2)R_G^2/2} \!+\!\,{\rm e}^{-({{q}}_{12}^2 +{{q}}_{14}^2+{{q}}_{24}^2)R_G^2/2} \\ &+\,{\rm e}^{-({{q}}_{13}^2 +{{q}}_{14}^2+{{q}}_{34}^2)R_G^2/2} +{\rm e}^{-({{q}}_{23}^2 +{{q}}_{24}^2+{{q}}_{34}^2)R_G^2/2} +{\rm e}^{-({{q}}_{12}^2+{{q}}_{34}^2)R_G^2/2} {\rm e}^{-({{q}}_{12}+{{q}}_{43})^2R_G^2/2} \\ &+\,{\rm e}^{-({{q}}_{14}^2+{{q}}_{23}^2)R_G^2/2} {\rm e}^{-({{q}}_{14}+{{q}}_{32})^2R_G^2/2}\Big) \!+\!{\rm e}^{-({{q}}_{12}^2+{{q}}_{24}^2+{{q}}_{43}^2+{{q}}_{31}^2)r_d^2/2} \Big( {\rm e}^{-({{q}}_{12}^2+{{q}}_{13}^2+{{q}}_{23}^2)R_G^2/2} \\ &+\,{\rm e}^{-({{q}}_{12}^2 +{{q}}_{14}^2+{{q}}_{24}^2)R_G^2/2} +{\rm e}^{-({{q}}_{13}^2 +{{q}}_{14}^2+{{q}}_{34}^2)R_G^2/2} +{\rm e}^{-({{q}}_{23}^2 +{{q}}_{24}^2+{{q}}_{24}^2)R_G^2/2} \\ &+\,{\rm e}^{-({{q}}_{13}^2+{{q}}_{24}^2)R_G^2/2} {\rm e}^{-({{q}}_{13}+{{q}}_{42})^2R_G^2/2} +{\rm e}^{-({{q}}_{12}^2+{{q}}_{34}^2)R_G^2/2} {\rm e}^{-({{q}}_{12}+{{q}}_{43})^2R_G^2/2}\Big) \\ &+\,{\rm e}^{-({{q}}_{13}^2 +{{q}}_{32}^2+{{q}}_{24}^2+{{q}}_{41}^2)r_d^2/2} \Big({\rm e}^{-({{q}}_{12}^2+{{q}}_{13}^2+{{q}}_{23}^2)R_G^2/2} +{\rm e}^{-({{q}}_{12}^2 +{{q}}_{14}^2+{{q}}_{24}^2)R_G^2/2} \\ &+\,{\rm e}^{-({{q}}_{13}^2 +{{q}}_{14}^2+{{q}}_{34}^2)R_G^2/2} +{\rm e}^{-({{q}}_{23}^2 +{{q}}_{24}^2+{{q}}_{34}^2)R_G^2/2} +{\rm e}^{-({{q}}_{13}^2+{{q}}_{24}^2)R_G^2/2} {\rm e}^{-({{q}}_{13}+{{q}}_{42})^2R_G^2/2} \\ & +\,{\rm e}^{-({{q}}_{14}^2+{{q}}_{23}^2)R_G^2/2} {\rm e}^{-({{q}}_{14}+{{q}}_{32})^2R_G^2/2}\Big)\bigg], \end{aligned} $

For a granular source with completely coherent pion-emission droplets, the factors
$ \lambda $ ,$ \xi $ , and$ \eta $ are zero, and the four-pion correlation function reduces to a simple formula [see Eq. (5)]. In this case, the maximum of$ C_4({{p}}_1, {{p}}_2,{{p}}_3,{{p}}_4) $ at$ {{q}}_{ij} = 0\; (i,j = 1,2,3,4) $ is n-dependent.
Analyses of multi-pion Bose-Einstein correlations for granular sources with coherent pion-emission droplets
- Received Date: 2020-06-29
- Available Online: 2021-02-15
Abstract: The ALICE Collaboration measured three- and four-pion Bose-Einstein correlations (BECs) for Pb-Pb collisions at the Large Hadron Collider (LHC). It is speculated that the observed significant suppression of multi-pion BECs is owing to a considerable degree of coherent pion emission in these collisions. Here, we study multi-pion BEC functions for granular sources with coherent pion-emission droplets. We find that the intercepts of the multi-pion correlation functions at the relative momenta near zero are sensitive to the number of droplets in the granular source. They decrease with the droplet number. The three-pion correlation functions for evolving granular sources with momentum-dependent partially coherent pion-emission droplets basically agree with the experimental data for Pb-Pb collisions at





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF














 DownLoad:
DownLoad: