-
The recent observations of exotic multi-quark states in the forms of tetra- and pentaquark systems in charmed and beauty meson and baryon sectors, respectively, demonstrate that there exist more complex configurations in nature than just quark-antiquark and three-quark systems – as already suggested by Gell-Mann in his pioneering presentation of the quark model [1]. A natural extension of complexity lies in hexaquark systems, which provide the transition to two-baryon, i.e., dibaryon systems.
Generally, dibaryons are solely defined by their baryon quantum number
$ B = 2$ . In this sense, we have known since 1932, when the deuteron was discovered [2], that at least a single one does exist. Owing to its very small binding energy of only 2.2 MeV, the deuteron constitutes a large extended hadronic molecule with a charge radius of 2.1 fm [3,4]. That is, the proton and the neutron inside the deuteron are, on average, 4 fm apart from each other and do not overlap.Since then, it has been continuously questioned whether there are more states in the two-baryon system than just the deuteron ground state with
$ I(J^P) = 0(1^+) $ . Follow-up nucleon-nucleon ($ NN $ ) scattering experiments revealed this state in the$ ^3S_1 $ partial wave to be the only bound state in the$ NN $ system. Its isovector counterpart, the virtual$ I(J^P) = 1(0^+) $ state in the$ ^1S_0 $ partial wave, was found to be already slightly unbound.With the recognition of quarks being the basic building blocks of hadrons, the idea of dibaryons being not just hadronic molecules but rather clusters ("sixpacks") of quarks sitting in a common quark bag stimulated the dibaryon search enormously. Manyfold quark models predicting a huge number of dibaryon states initiated a rush of experimental searches for such objects. Unfortunately, practically, none of the many claims for experimental evidence have survived rigorous experimental checks. For a review of the history of dibaryon predictions and searches, see, e.g., Ref. [5].
This situation changed approximately 10 years ago, when the CELSIUS/WASA [6] and the WASA-at-COSY collaborations [7,8] started to report their experimental results obtained in a series of experiments on two-pion production in
$ NN $ collisions and in neutron-proton scattering. In all relevant two-pion channels, the Lorentzian energy dependence of a narrow isoscalar resonance – named$ d^*(2380) $ – was observed. By measurement of polarized proton-neutron scattering and its inclusion in the phase-shift analysis, a circular counter-clockwise movement in the$ ^3D_3 $ partial wave was revealed establishing a pole with$ I(J^P) = 0(3^+) $ at approximately 2380 MeV [9,10]. From these investigations, the branching ratios of$ d^*(2380) $ were determined for all its hadronic decays [11].In the following chapters, Ⅱ and Ⅲ, a short review is provided starting from the first solid observation of
$ d^*(2380) $ in the double-pionic fusion measurements at CELSIUS/WASA [6] and WASA-at-COSY [7] up to its current status in hadronic and electromagnetic excitation and decay processes. In chapter Ⅳ, the status of theoretical work on$ d^*(2380) $ is reviewed with emphasis on the width issue and the key question, i.e., whether it constitutes a compact hexaquark or a dilute molecular system.Chapter Ⅴ deals with resonance structures at
$ \Delta(1232)N $ and$ N^*(1440)N $ thresholds pointing to dibaryonic states of molecular character – in analogy to the situation for tetra- and pentaquark systems in the charm and beauty sectors. Finally, the current dibaryon situation in flavored quark sectors is briefly discussed in chapter Ⅵ. -
Resonances in single- and two-baryon systems decay preferentially by emission of one or several pions. Hence, pion production in
$ NN $ collisions gives access to the physics of resonances both in baryon and dibaryon systems. The latter systems are of particular interest here. The oldest prediction of six-quark objects decaying by pion emission dates back to the report by Dyson and Xuong [12], who – based on SU(6) symmetry considerations – predicted the existence of six non-strange dibaryon states.As there existed no detailed database on pion production in
$ NN $ collisions, a systematic study – in particular, of two-pion production – started in the nineties at CELSIUS and was continued subsequently at COSY using the hermetic WASA detector. All CELSIUS/WASA and WASA-at-COSY measurements on single- and multiple-pion production reported here were carried out exclusively and kinematically complete – in most cases, kinematically over-constrained in order to improve the momentum resolution by kinematic fits and to provide data free of background. -
The search for resonances in the system of two baryons dates back to the fifties, when first measurements of the
$ \pi d \to pp $ reaction at Dubna [13-15] indicated a resonance-like structure near the$ \Delta N $ threshold connected to the$ ^1D_2 $ partial wave in the$ NN $ system. Subsequently, high quality data on total and differential cross sections and polarization observables for$ pp $ and$ \pi d $ elastic scattering as well as$ \pi d \to pp $ and$ pp \to \pi d $ reactions revealed a pronounced looping of the$ ^1D_2 $ $ NN $ partial wave in the Argand diagram representing a pole of a resonance with$ I(J^P) = 1(2^+) $ , mass$ m \approx $ 2148 MeV, and width$ \Gamma \approx 120\;{\rm{ MeV}} $ [16,17].Though the clear looping is in favor of a true s-channel resonance, the close neighborhood of its mass to that of the
$ \Delta N $ threshold and the compatibility of its width with that of$ \Delta(1232) $ cast doubts on its s-channel nature. It has been argued that the observed features could be merely a threshold phenomenon and the observed looping just a reflection of the usual$ \Delta $ excitation process in the presence of the other nucleon, which, owing to the threshold condition, must be at rest relative to the active one.The situation regarding this resonance structure has been controversial in many papers, see, e.g., [5]. In a number of publications, Hoshizaki demonstrated that this resonance structure constitutes a true S-matrix pole rather than a threshold cusp or virtual
$ \Delta N $ state [18,19]. Similar conclusions were reported by Ueda et al. [20].The resonance structure seen in the
$ ^1D_2 $ $ NN $ -partial wave is by far the most pronounced one seen in$ NN $ scattering and$ \pi d \rightleftharpoons NN $ reactions. In other partial waves, a resonant behavior had also been noted in the region of the$ \Delta N $ threshold, though not as spectacular by far. In partial wave solutions of the SAID analysis group, e.g., the$ ^3P_2- ^3F_2 $ ,$ ^3F_3 $ , and$ ^3F_4- ^3H_4 $ $ NN $ -partial waves also exhibit a clear looping in the Argand diagram [16,17,21].The fact that all these states near the
$ \Delta N $ threshold exhibit a width close to that of$ \Delta(1232) $ is not too surprising, as the available phase space of a$ \Delta N $ state for a fall-apart decay into its components$ N $ and$ \Delta $ is small, close to the$ \Delta N $ threshold, and hence, the only sizeable decay contribution arises from the decay of the component$ \Delta $ . We will return to the discussion of states near thresholds in chapter V. In the next chapters, first, the situation of the hitherto reported sole example of a deeply bound (relative to the$ \Delta\Delta $ threshold) dibaryon state,$ d^*(2380) $ , will be reviewed. -
The two-pion production program at CELSIUS started out in 1993 with exclusive and kinematically complete high-statistics measurements of
$ pp $ -induced two-pion production from the threshold region up to the GeV region.As a result of these systematic studies, it was found that isovector induced two-pion production up to
$ \sqrt s \approx $ 3 GeV is well described by the conventional process of$ t $ -channel meson exchange leading to the excitation of the$ N^*(1440) $ Roper resonance and the excitation of the$ \Delta(1232)\Delta(1232) $ system. The first process dominates at lower beam energies close to the threshold, whereas the latter one dominates at energies above 1 GeV, i.e.,$ \sqrt s $ > 2.4 GeV.This conclusion also includes the isovector double-pionic fusion process
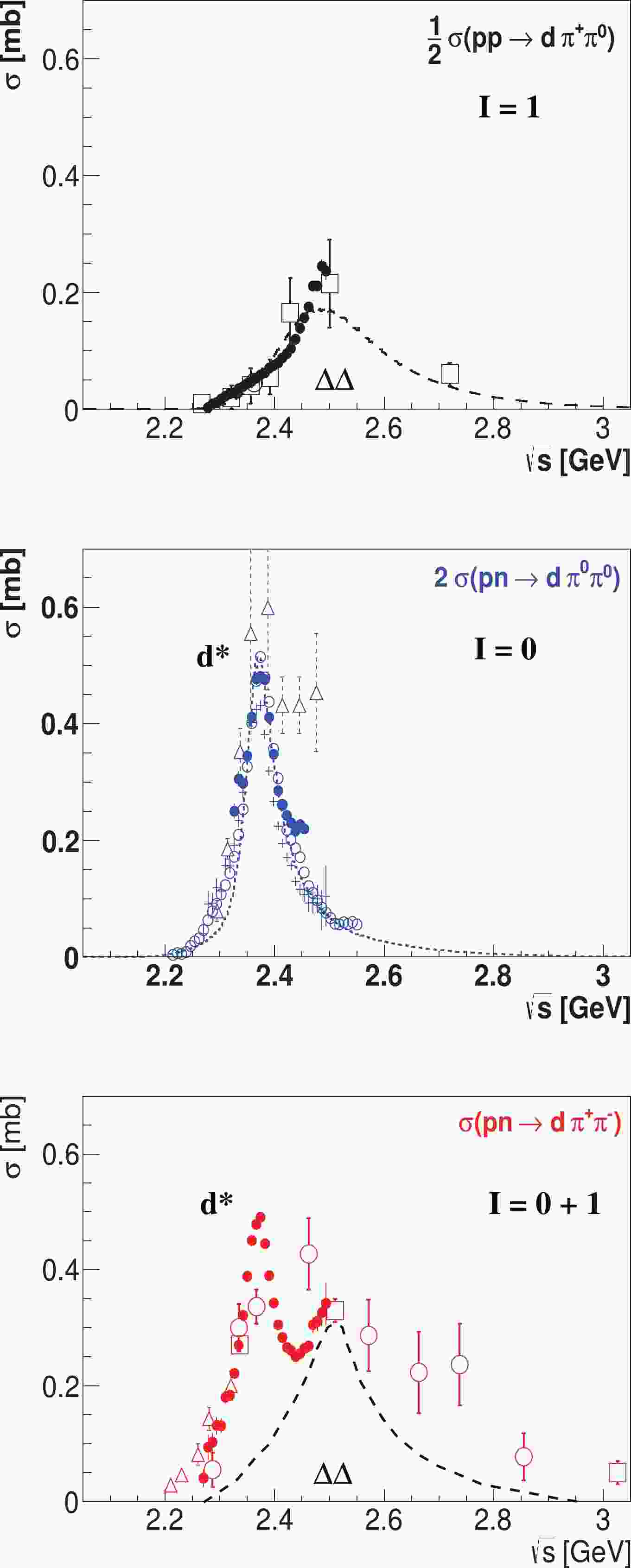
$ pp \to d\pi^+\pi^0 $ . Measurements of its differential cross sections in the region$ \sqrt s \approx $ 2.4 GeV are in good agreement with$ t $ -channel$ \Delta\Delta $ calculations, and the energy dependence of its total cross section exhibits a broad resonance-like structure with a width of approximately 2$ \Gamma_\Delta $ in accord with the$ t $ -channel$ \Delta\Delta $ calculations [8,22] – see the top panel of Fig. 1.
Figure 1. (color online) Total cross section of the double-pionic fusion to deuterium and its isospin decomposition. Top panel: the isovector part of the
$ pn \to d\pi^+\pi^- $ reaction given by half the cross section of the$ pp \to d\pi^+\pi^0 $ reaction. Solid dots show WASA-at-COSY [8] results and open symbols indicate previous results [22-24]. The dashed curve represents a$ t $ -channel$ \Delta\Delta $ calculation fitted in height to the data [22]. Middle panel: The isoscalar part of the$ pn \to d\pi^+\pi^- $ reaction given by twice the cross section of the$ pn \to d\pi^0\pi^0 $ reaction. The CELSIUS/WASA results [6] are shown by open triangles. The other symbols refer to WASA-at-COSY measurements [7,8]. The dotted line denotes the$ d^* $ resonance curve with momentum dependent widths [25], mass m = 2370 MeV, and total width$ \Gamma $ = 70 MeV. Bottom panel: the isospin-mixed reaction$ pn \to d\pi^+\pi^- $ . Solid dots represent WASA-at-COSY measurements, open symbols represent previous bubble-chamber measurements at DESY (circles) [26], Dubna (squares) [27], and Gatchina (triangles) [28]. The dashed line represents the$ t $ -channel$ \Delta\Delta $ excitation. From Ref. [8]. -
When
$ pn $ -induced two-pion production was observed, the situation changed strikingly. The measurements were carried out with either a deuteron beam or deuterium target by taking advantage of the quasi-free process, e.g., by looking on the process$pd \to d\pi^0\pi^0 + p_{\rm spectator}$ within the$ pd \to dp\pi^0\pi^0 $ reaction. Because all these measurements were exclusively and kinematically complete (in most cases, even over-constrained, allowing kinematic fitting, thus improving the resolution and purity of the collected events), the effective total energy of the$ pn \to d\pi^0\pi^0 $ subprocess was known on an event-by-event basis. Thus, the energy dependence of the quasi-free process could be measured over an appropriate energy range with a single beam energy setting.For the
$ d\pi^0\pi^0 $ channel, there were no previous measurements at all, as a hermetic detector such as WASA with its capability to detect both charged and uncharged particles over a solid angle of nearly$ 4\pi $ was not available at other installations for hadron research.By use of isospin relations [23,27] and isospin recoupling in case of an intermediate
$ \Delta\Delta $ system [5], the cross section of the$ t $ -channel$ \Delta\Delta $ process in the$ d\pi^0\pi^0 $ channel can be determined to be only 1/5 of that in the$ d\pi^+\pi^0 $ channel, i.e., approximately 0.04 mb at$ \sqrt s \approx $ 2.5 GeV, where the$ t $ -channel$ \Delta\Delta $ process peaks. Owing to this low cross section of conventional processes, this reaction channel is predestinated for the observation of unconventional isoscalar processes, so to speak, the "golden" channel.The measurements for this channel [6-8], displayed in the middle panel of Fig. 1 as well as in Fig. 2, indeed revealed the cross section around 2.5 GeV to be of this magnitude. However, the big surprise was that, at lower energies, a much larger cross section was observed to exhibit a pronounced narrow resonance-like structure, which can be very well fitted by a Breit-Wigner ansatz with momentum dependent widths [25], mass m = 2370 MeV, and total width
$ \Gamma $ = 70 MeV – see the dotted line in the middle panel of Fig. 1.
Figure 2. (color online) Measurements of the "golden" reaction channel
$ pn \to d\pi^0\pi^0 $ with WASA at COSY. Top: total cross section exhibiting the pronounced resonance structure. The blue open symbols show the data of Ref. [7]. They have been normalized in absolute scale to the data of Ref. [8], which are plotted with red stars. The black shaded area represents an estimate of the systematic uncertainties. The solid curve shows a calculation of the$ d^*(2380) $ resonance with momentum-dependent widths according to Ref. [25] and including$ t $ -channel Roper and$ \Delta\Delta $ excitations as background reactions. The filled circles represent the difference between this calculation and the data in the low-energy tail of$ d^*(2380) $ . Middle: deuteron angular distribution (left) and Dalitz plot (right) at the peak energy of$ \sqrt s $ = 2.38 GeV. Open and solid circles refer to measurements with the spectator proton in the target and in the beam (reversed kinematics), respectively. The dashed curve gives a Legendre fit with$L_{\max}$ = 6 corresponding to J = 3. Bottom: Dalitz plot projections yielding the distributions of the squares of the$ d\pi^0 $ - (left) and$ \pi^0\pi^0 $ - (right) invariant masses. The low-mass enhancement in the latter spectrum denotes the ABC effect. The solid lines represent a calculation of the$ pn \to d^*(2380) \to \Delta^+\Delta^0 \to d\pi^0\pi^0 $ process. From Refs. [7,29,30].The measurement of the deuteron angular distribution displayed in Fig. 2 led to a
$ J $ = 3 assignment for the resonance structure [7]. Together with the isoscalar character of the$ pn \to d\pi^0\pi^0 $ reaction, this gives the isospin-spin-parity combination$ I(J^P) = 0(3^+) $ . Owing to its isoscalar character and the baryon number$ B = 2$ , the resonance structure is formally compatible with an excited state of the deuteron; hence, it is denoted as$ d^* $ .The Dalitz plot and its mass-squared projections are shown in Fig. 2. Together with the
$ N\pi^0 $ angular distribution [7], they suggest a$ \Delta\Delta $ configuration in relative$ s $ -wave as an intermediate configuration, which, according to the observed mass of 2370 MeV, must be bound by approximately 90 MeV relative to the nominal$ \Delta\Delta $ threshold mass of 2464 MeV [7].In measurements of the
$ pn \to d\pi^+\pi^- $ reaction (bottom panel of Fig. 1) and the isospin decomposition [8,23,28] of its cross section according to the relation$ \sigma (pn \to d\pi^+\pi^-) = 2\sigma(pn \to d\pi^0\pi^0) + \frac1 2 \sigma(pp \to d\pi^+\pi^0), $

(1) it has been demonstrated that the resonance structure appears only in the isoscalar part of the double-pionic fusion to the deuteron and not in its isovector part, i.e., it has a definite isospin
$ I $ = 0. -
The pronounced low-mass enhancement observed in the Dalitz plot and its projection onto the
$ \pi\pi $ -invariant mass-squared, as displayed Fig. 2, is remarkable. In fact, such low-mass enhancements had been noticed already in double-pionic fusion experiments. Actually, they laid the trace for the discovery of$ d^* $ at WASA [5,31].In 1960, Abashian, Booth, and Crowe [32] noticed an enhancement in the 3He missing mass spectrum of the inclusively measured
$ pd \to ^3{\rm{HeX}} $ reaction. This enhancement occured just in the kinematic region corresponding to the emission of two pions with low$ \pi\pi $ -invariant mass. Follow-up measurements revealed this enhancement to occur in the double-pionic fusion reactions$ pn \to d\pi\pi $ ,$ pd \to ^3{\rm{He}} \pi\pi $ , and$ dd \to ^4{\rm{He}}\pi\pi $ , but not in the fusion to 3H, where an isovector pion pair is emitted.In all the years since then, no conclusive explanation could be presented for the observed low-mass enhancement in spite of many theoretical attempts. Hence, it was simply abbreviated as "ABC" effect in literature using the initials of the authors Abashian, Booth, and Crowe, who noticed this enhancement first.
The WASA measurements of the complete double-pionic fusion to the deuteron comprising all three reactions
$ pp \to d\pi^+\pi^0 $ ,$ pn \to d\pi^0\pi^0 $ , and$ pn \to d\pi^+\pi^- $ deciphered this effect to be stringently correlated with the appearance of the isoscalar resonance structure$ d^* $ [7,8,22] in double-pionic fusion processes. There, the ABC effect merely reflects the vertex function of the decay vertex$ d^* \to \Delta\Delta $ and shows up in the$ \pi\pi $ invariant mass spectrum only, if the nucleons in the final state fuse to a bound system [25]. Subsequent WASA experiments showed that the dibaryon resonance$ d^* $ is formed in the double-pionic fusions to 3He and 4He, too, though it appears much broadened there due to collision damping with the surrounding nucleons [5,33,34]. -
Recently, the non-fusion two-pion production reactions
$ pn \to pp\pi^0\pi^- $ [35],$ pn \to pn\pi^0\pi^0 $ [36], and$ pn \to pn \pi^+\pi^- $ [37] have also been investigated. All these channels are isospin-mixed, i.e., contain both isoscalar and isovector contributions. Hence, the$ d^* $ signal appears just on top of a substantial and – due to its four-body character – steeply rising background of conventional processes. Nevertheless, it still shows up clearly in the energy dependence of the total cross sections for these reaction channels.By using the isospin-decomposition of
$ NN $ -induced two-pion production [5,23,28], the expected size of the$ d^* $ contribution in these channels can be easily estimated. A more detailed treatment also takes into account the different phase-space situations when the deuteron is replaced by the unbound$ pn $ system in these reactions [38,39].In summary, all
$ NN $ -induced two-pion production channels are in accordance with the appearance of an$ I(J^P) = 0(3^+) $ dibaryon resonance at 2.37 GeV with a width of 70 MeV. Even in the channels, which are only partially isoscalar, the$ d^* $ contribution is still the dominating process. The conventional$ t $ -channel processes there underpredict the data in the$ d^* $ energy region by factors of two to four [35-37]. -
If the resonance structure
$ d^* $ observed in two-pion production indeed is a true$ s $ -channel resonance, it must show up in principle in the entrance channel as well, i.e., in the$ np $ scattering channel. There, it must produce a pole in the partial waves corresponding to$ I(J^P) = 0(3^+) $ , i.e., in the coupled partial-waves$ ^3D_3 $ -$ ^3G_3 $ .The expected resonance contribution to the elastic
$ np $ scattering can be calculated from the knowledge of the resonance contributions to the various two-pion production channels under the assumption that there is no decay into the isoscalar single-pion production channel, which is forbidden in leading order in the case of an intermediate$ \Delta\Delta $ formation. In Ref. [11] this resonance contribution has been estimated to be approximately 170$\mu{\rm{b}}$ , which is small compared to the value of nearly 40 mb for the total$ np $ cross section.The analyzing power angular distribution of the elastic scattering is a particularly suitable observable to sense such a small contribution of
$ d^*(2380) $ , as it is composed only of interference terms in the partial waves and hence sensitive to even small terms in the coupled$ ^3D_3 - ^3G_3 $ partial waves. In the angular distribution of the analyzing power, the contribution of a resonance with$ J = 3$ is given by the angular dependence of the associated Legendre polynomial$ P^1_3 $ . Therefore, the resonance contribution is expected to be the largest at 90°, which is also the angle where the differential cross section is the smallest. For the sensitivity of other observables to the$ d^* $ resonance, see Ref. [10].In the region of interest for the
$ d^* $ issue, there existed no analyzing power data from previous measurements. Precise measurements at SACLAY ended just below the$ d^* $ region [40,41]. Hence, corresponding analyzing power measurements extending over practically the full angular range were undertaken with WASA at COSY – again in the quasi-free mode. By use of inverse kinematics, a polarized deuteron beam was directed onto the hydrogen pellet target [9,42].The WASA data are shown in Fig. 3 together with the previous measurements [40, 41, 43-48]. The top panel displays the energy dependence of the analyzing power near a center-of-mass scattering angle of 90
$ ^\circ $ , where the$ d^* $ resonance effect is expected to be largest. A pronounced narrow resonance-like structure is observed in the data at the$ d^* $ energy position. Accordingly, the measured angular distribution of the analyzing power, displayed in the middle panel of Fig. 3, deviates from the conventionally expected distribution the largest in the 90° region. In both panels, the solid line shows the solution SP07 from the SAID partial-wave analysis prior to the WASA measurements [49].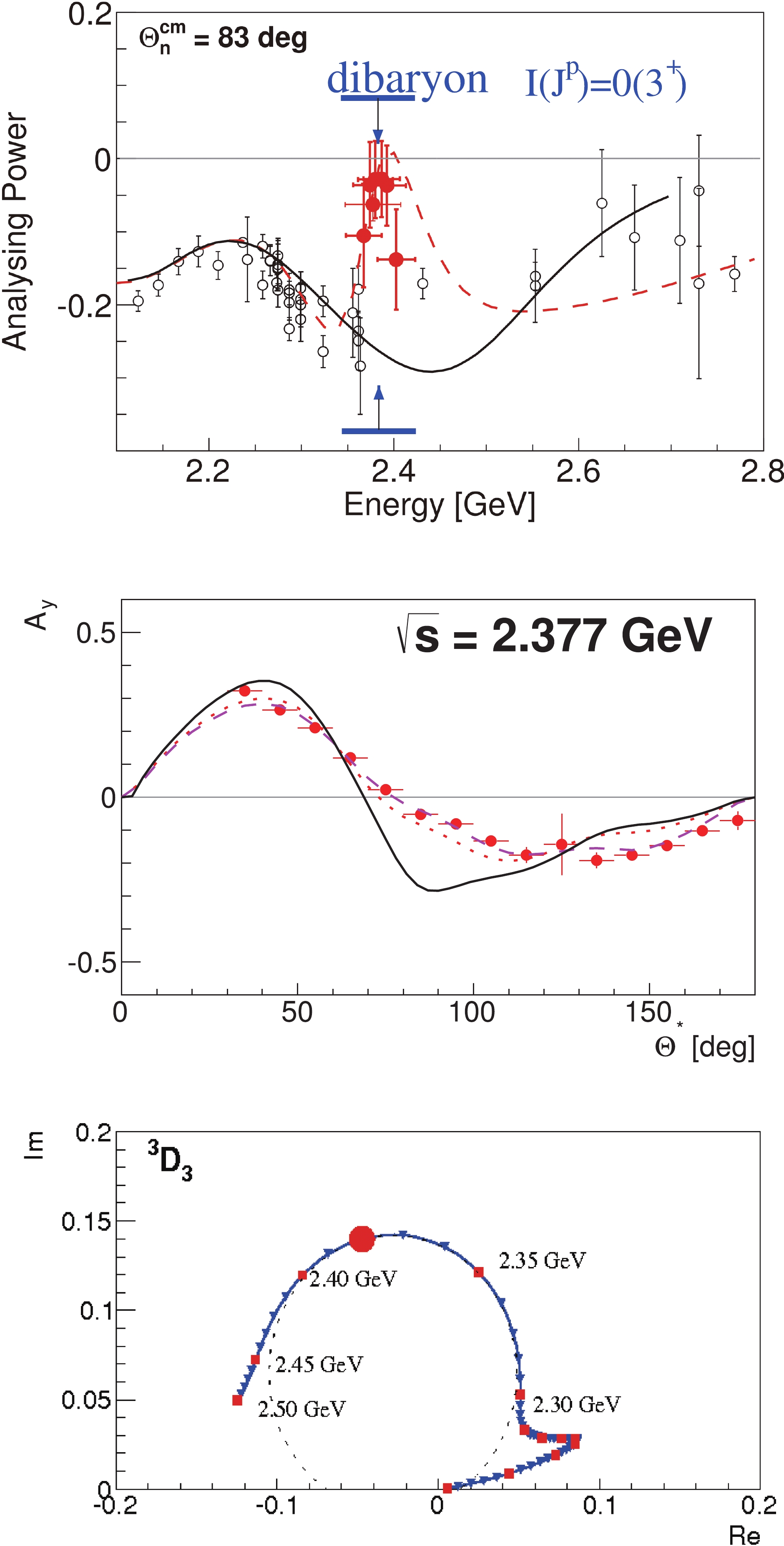
Figure 3. (color online) Analyzing power data for elastic
$ pn $ scattering in the$ d^*(2380) $ energy region and their partial-wave analysis [9,10,42]. Top: energy dependence of the analyzing power in the vicinity of$ \Theta_n^{cm} = 90^\circ $ , where the effect of the$ d^*(2380) $ resonance is expected to be the largest. The solid circles denote WASA results, and the open symbols represent previous data [40, 41, 43-48]. The solid line gives the previous SAID partial-wave solution, and the dashed line gives the new SAID solution after including the WASA data. Middle: Angular distribution of the analyzing power$ A_y $ at the resonance energy. The curves have the same meaning as in the top figure. Bottom: Argand diagram of the new SAID solution for the$ ^3D_3 $ partial wave with a pole at 2380 MeV. The thick solid circle denotes the pole position. From Ref. [5]The subsequent partial-wave analysis results by the SAID group including the WASA data are given by the dashed and dotted lines in the top and middle panels, respectively. This partial-wave solution, denoted as AD14, finds a pole in the coupled
$ ^3D_3 - ^3G_3 $ partial waves at the position$(2380\pm10)-{\rm i}(40\pm5)$ MeV, which is in full agreement with the findings in the two-pion production reactions [9,10,42]. The bottom panel in Fig. 3 displays the Argand diagram of the new solution AD14 for the$ ^3D_3 $ partial wave. It exhibits a pronounced looping of this partial wave in agreement with a resonant behavior. The poles in$ ^3D_3 $ and$ ^3G_3 $ partial waves have been reproduced in a theoretical study of nucleon-nucleon scattering within the constituent quark models of the Nanjing group [50].Very recently, data for the differential cross sections of the
$ pn $ scattering in the region of$ d^*(2380) $ could also be extracted from the WASA database. It turned out that the new experimental data are perfectly described by the AD14 partial-wave solution, which is a remarkable success that furthers confidence in the uniqueness and predictive power of this solution [51].With this result, the resonance structure observed in two-pion production has been established as a genuine
$ s $ -channel resonance in the proton-neutron system. Owing to its isoscalar character, the notation$ d^*(2380) $ has been chosen in analogy to the denotation for isoscalar excitations of the nucleon. -
From the various two-pion production measurements as well as from the
$ np $ scattering experiments and their analysis, the branching ratios given in Table 1 have been extracted for the hadronic decays of$ d^*(2380) $ [5,11]. The decay into the unmeasured$ nn\pi^+\pi^0 $ channel has been taken to be identical to that into the$ pp\pi^o\pi^- $ channel by isospin symmetry.decay channel experiment theory [52,58] $ NN\pi\pi $ isospin recoupling

$ d\pi^0\pi^0 $ 

$ 14\pm1 $ 

12.8 13 $ d\pi^+\pi^- $ 

$ 23\pm2 $ 

23.4 26 $ np\pi^0\pi^0 $ 

$ 12\pm2 $ 

13.3 13 $ np\pi^+\pi^- $ 

$ 30\pm5 $ 

28.6 32.5 $ pp\pi^0\pi^- $ 

$ 6\pm1 $ 

4.9 6.5 $ nn\pi^+\pi^0 $ 

$ 6\pm1 $ 

4.9 6.5 $ (NN\pi)_{I=0} $ 

<5(90% C.L.) 0.9 – $ np $ 

$ 12\pm3 $ 

12.1 – $ d\gamma $ 

$ \approx $ 0.01

$\sum({\rm total})$ 

$ 103\pm7 $ 

100 Table 1. Branching ratios in percent of the
$ d^*(2380) $ decay into$ pn $ ,$ NN\pi $ ,$ NN\pi\pi $ , and$ d\gamma $ channels. The experimental results [11,53-57] are compared to those from theoretical calculations [52,58], starting from the theoretical$ d^* $ wave function and including isospin breaking effects. They are also compared to the values expected from pure isospin recoupling of the various$ NN\pi\pi $ channels. In the latter case, the branching into the$ d\pi^0\pi^0 $ channel is normalized to the data.The observed
$ d^* $ decay branchings into the diverse two-pion channels are consistent with those expected from isospin decomposition [11] as well as explicit QCD model calculations [52].In a dedicated WASA search for the hypothetical decay
$ d^*(2380) \to (NN\pi)_{I = 0} $ , no signal from$ d^*(2380) $ could be sensed in the experimental isoscalar single-pion production cross section, but an upper limit of 5% at 90% C.L. could be derived for such a branching [53,54]. Note that, in Ref. [53], the upper limit was given too high by a factor of two [54]. This result strongly disfavors models predicting a molecular structure for$ d^*(2380) $ [59-62] but is in full accord with a compact hexaquark-$ \Delta\Delta $ structure [58].It should be pointed out that the successful reproduction of all hadronic decay branchings of
$ d^*(2380) $ and its total width by the theoretical calculations also means that all experimentally observed cross sections in the various hadronic channels are understood theoretically in a quantitative manner. -
The electromagnetic decay channels are very interesting, as they offer the possibility to excite the resonance also by photo- and electro-production. The latter, in particular, offers the possibility to measure that way the transition form-factor, which could give experimental access to the size of
$ d^*(2380) $ and thus further clarify the question about the structure of$ d^*(2380) $ . From the$ \gamma $ decay of the$ \Delta $ resonance, one may estimate that the cross sections for the processes$ pn \to d^*(2380) \to \Delta\Delta \to d\pi^0\gamma $ and$ pn \to d^*(2380) \to \Delta\Delta \to d\gamma\gamma $ are smaller than those corresponding to the hadronic decays by two and four orders of magnitude, respectively. For the$ d\gamma $ decay channel, the situation is presumably similar.A possible indication of
$ d^*(2380) $ photo-excitation has been observed already in the seventies in the photo-absorption reaction$ \gamma d \to pn $ by measuring the polarization of the ejected protons. After observation [63,64] of an anomalous structure in the proton polarization from deuteron photodisintegration, Kamae and Fujita [65] suggested the possible existence of a deeply bound$ \Delta\Delta $ system with$ I(J^P) = 0(3^+) $ at$ \sqrt s $ = 2.38 GeV with a width of 160 MeV. Subsequent analyses based on an increased basis of polarization measurements yielded the possible existence of at least two dibaryon resonances with either$ I(J^P) = 0(3^+) $ or$ 0(1^+) $ at$ \sqrt s $ = 2.38 GeV and$ I(J^P) = 1(3^-) $ or$ 1(2^-) $ at$ \sqrt s $ = 2.26 GeV with widths of 200 MeV and above [66,67].New measurements of the
$ \gamma d \to pn $ reaction with polarized photons at MAMI – also measuring for the first time the polarization of the emerging neutrons – are consistent with an excitation of$ d^*(2380) $ in this process [68,69]. At the photon energy corresponding to the$ d^*(2380) $ mass, both the previously measured proton polarization [66,67,70] and the newly measured neutron polarization peak at a scattering angle of 90 degrees in the center-of-mass system, where they reach a polarization of$ P_y $ = −1. This extreme value means that the final pn system must be in a spin triplet state as required for a$ d^*(2380) \to pn $ decay. The measured [69] energy dependence of$ P_y $ at 90 degrees is in agreement with a Lorentzian energy dependence having the width of$ d^*(2380) $ .Very recently, the first report on data for the
$ \gamma d \to d\pi^0\pi^0 $ reaction also appeared, reaching in energy down to the$ d^*(2380) $ region. The measurements conducted at ELPH, Japan, only reach down to the high-energy side of the$ d^*(2380) $ region [55,56]. Measurements performed at MAMI even reach below the$ d^* $ region [57]. Both measurements must fight heavily with background contributions at the lowest energies. However, both measurements find a surplus of cross section in the$ d^* $ region in comparison to the state-of-the-art calculations of Fix and Arenhövel [71,72], which describe the data very well above$ \sqrt s $ = 2.40 GeV. A$ d^* $ cross section of approximately 20 nbarn provides a good description of both data sets in the$ d^* $ region. This is just four orders of magnitude smaller than the cross section in the corresponding hadronic channel providing an electromagnetic branching of$ 10^{-4} $ for the$ d^*(2380) \to d\gamma $ transition – in agreement with the estimate given above. First attempts to understand the photo-absorption process$ \gamma d \to d^*(2380) $ theoretically [73,74] provided cross sections that were too low by an order of magnitude. -
There have been a huge number of dibaryon predictions in the past. The oldest one dates back to 1964, when based on SU(6) symmetry considerations, Dyson and Xuong [12] predicted six non-strange dibaryon states
$ D_{IJ} $ , where the indices denote isospin I and spin J of the particular state. They identified the two lowest-lying states$ D_{01} $ and$ D_{10} $ with the deuteron ground state and the virtual$ ^1S_0 $ state, respectively, the latter being known from low-energy$ NN $ scattering and final-state interaction. Identifying in addition the third state$ D_{12} $ with the already debated (at that time) resonance-like structure at the$ N\Delta $ threshold having$ I(J^P) = 1(2^+) $ , they fixed all parameters in their mass formula. As a result, they predicted a state$ D_{03} $ with just the quantum numbers of$ d^*(2380) $ at a mass of 2350 MeV, which is remarkably close to the now observed$ d^* $ mass. The remaining predicted states are$ D_{21} $ and$ D_{30} $ . Owing to their isospins I = 2 and 3, they are$ NN $ -decoupled. According to Dyson and Xuong, they should have masses very similar to those of$ D_{12} $ and$ D_{03} $ , respectively.On the one hand, it appears remarkable how well the prediction of Dyson and Xuong works. On the other hand, this may not be too surprising, because we know that the mass formulas for baryons and mesons derived from symmetry-breaking considerations also perform remarkably well if a few phenomenological parameters are adjusted to experimental results.
Oka and Yazaki were the first to apply the nonrelativistic quark model to the problem of the nuclear force. They demonstrated that the interplay between the Pauli principle and the spin-spin interaction between quarks leads to a strong short-range repulsion between nucleons but to an attractive force for a
$ \Delta\Delta $ system with$ I(J^P) = 0(3^+) $ [75].Terry Goldman, Fan Wang, and collaborators [76] pointed out later that a
$ \Delta\Delta $ configuration with the particular quantum numbers of$ d^*(2380) $ must have an attractive interaction due to its special color-spin structure, so that any model based on confinement and effective one-gluon exchange must predict the existence of such a state – the "inevitable dibaryon" as they called it. In their quark-delocalization and color-screening model (QDCSM), they initially predicted a binding energy of 350 MeV relative to the nominal$ \Delta\Delta $ threshold, but it approached the experimental value in more recent works [50,77,78].In fact, many groups also calculated such a state at similar masses based either on quark-gluon [77-89] or hadronic interactions [59,60,65]. Already, the early bag-model calculations of the Nijmegen theory group [85,86], including the work of Mulders and Thomas [87] and Saito [88], predicted
$ d^*(2380) $ at approximately the correct mass. However, in these calculations, numerous other unflavored dibaryon states were also predicted that have not been observed (at least so far) or have been observed at a significantly different mass, e.g., the$ D_{12} $ state.Another correct real prediction, i.e., a prediction before the experimental observation of
$ d^*(2380) $ , is that by the IHEP theory group led by Z. Y. Zhang, who studied this state in the chiral SU(3) quark model within the resonating group method [79]. This work and follow-up investigations of this group [80-83] include the concept of "hidden color". Hidden-color six-quark states are a rigorous first-principle prediction of SU(3) color gauge theory. Six quark color-triplets$ 3_c $ combine into five different color-singlets in QCD and significantly decay to$ \Delta\Delta $ , as shown in Refs. [90,91]. Problems related to the application of hidden color in multi-quark systems have been discussed by Fan Wang et al. [92]. They point out that, although the$ \Delta\Delta $ and hidden-color configurations are orthogonal for large separations between the two quark clusters, they loose their orthogonality when they start to overlap at small separations. Another point of caution has been noted by F. Huang and W.L. Wang in Ref. [93]. In this work, they study the masses of octet and decuplet baryon ground states, the deuteron binding energy, and the$ NN $ scattering phase shifts (for$ J\leqslant $ 6) below the pion-production threshold within a chiral SU(3) quark model. They demonstrate that all of these can be described well if the consistency requirement for the single-baryon wave functions to satisfy the minima of the Hamiltonian are strictly imposed in the determination of the model parameters. In earlier quark-model calculations, usually, the nucleon is set to be at the minimum of the Hamiltonian by a particular choice of the model parameters. As a consequence, the$ \Delta $ , which is of different size, is not stable against its size parameter in the wave function, i.e., its wavefunction is not the real solution of the Hamiltonian. Hence, one needs to be very careful when extending the model from the study of the NN interaction to other baryon-baryon systems, and one may need to introduce additional channels such as the hidden-color channel to lower the energy of the$ \Delta\Delta $ system. These channels may not be the physical ones but are partially needed to change the internal wave function of the single$ \Delta $ . Therefore, one must be cautious in explaining the configuration structure of the coupled$ \Delta\Delta $ -hidden-color system. Hence, the IHEP result of 2/3 hidden-color components in$ d^*(2380) $ must be taken with some caution with regard to its interpretation of the configuration of$ d^*(2380) $ . An improved calculation for$ d^*(2380) $ with a consistent treatment of the$ \Delta\Delta $ system is in progress [94].Recently, a diquark model has also been proposed for
$ d^*(2380) $ [95]. In this work, it is assumed that$ d^*(2380) $ is composed of three vector diquarks, and its mass is calculated by use of an effective Hamiltonian approach. Surprisingly, in this rough and simple model, both mass and width (see next subsection) turn out to be in good agreement with the experimental data. In a subsequent paper [96], Gal and Karliner questioned the applicability of diquark models in the light-quark sector by demonstrating that the use of the effective Hamiltonian with parameters given in Ref. [95] leads to masses for deuteron- and virtual-like states, which are 200-250 MeV above the physical deuteron and the virtual$ ^1S_0 $ state. However, as pointed out in a reply, the latter two states interpreted as three-axial-vector-diquark states reside in spin-flavor multiplets different from the one of$ d^*(2380) $ and need a Hamiltonian with more interactions included [94].As a historic side remark, we note that a diquark model for a deuteron-like object had been proposed earlier [97], where three scalar diquarks were coupled in relative
$ P $ -wave to an isoscalar$ J^P = 0^- $ object, the "demon deuteron" possessing a highly suppressed decay. In this context, the data for$ np \to d\pi^+\pi^- $ , which were available at that time, indicating a peak in the total cross section around$ \sqrt s \approx $ 2.3 GeV, and exhibiting the ABC effect (see section IIC.1), were interpreted as evidence for the existence of such a "demon deuteron." As we now know, this turns out to be just the place where$ d^*(2380) $ was found instead.Meanwhile, also a QCD sum rule study found this state at the right mass [89], whereas another QCD-based work without any inclusion of hadron degrees of freedom could construct such a state as a compact object only at much higher masses [98].
Most recently, the first lattice QCD calculations for
$ d^*(2380) $ were presented by the HAL QCD collaboration [99,100], finding evidence for a bound$ \Delta\Delta $ system with the quantum numbers of$ d^*(2380) $ . In these calculations, the pion mass is still unrealistically large, as$ \Delta(1232) $ must be assumed to be a stable particle to make such calculations feasible at present. Therefore, the lattice results were recently extrapolated down to the real pion mass by methods based on the Effective Field Theory with the result that, indeed, such a bound state is likely to exist [101].Gal and Garcilazo also obtained this state at the proper mass in recent relativistic Faddeev calculations based on hadronic interactions within a baryon-baryon-pion system [59,60] and assuming a decay
$ d^*(2380) \to D_{12}\pi \to \Delta N \pi $ . Such a decay was also investigated by Kukulin and Platonova [61,62]. -
More demanding than the mass value appears to be the reproduction of the small decay width of
$ d^*(2380) $ . As worked out in a paper together with Stanley Brodsky [102], the small width points to an unconventional origin, possibly indicating a genuine six-quark nature. With the dominant decay being$ d^*(2380) \to \Delta\Delta $ , one would naively expect a reduction of the decay width from$ \Gamma_{\Delta\Delta} $ = 240 MeV to 160 MeV for a$ \Delta\Delta $ system bound by 90 MeV using the known momentum dependence of the width of the$ \Delta $ resonance. This is twice the observed width. In contrast, if$ d^*(2380) $ is a genuine six-quark state, we need to understand its large coupling to$ \Delta\Delta $ . This can be explained, if one assumes that$ d^*(2380) $ is dominated by "hidden-color" configurations.So far, there have been five predictions for the decay width based on Faddeev calculations [59,60], quark-model calculations [52,77,78,82,83,95,103,104], or some general considerations [106]. A width of 160 MeV, as discussed above, is also obtained initially in the quark-model calculations of Fan Wang et al. [77]. By accounting for correlations in a more detailed treatment, they finally arrive at 110 MeV [78], and a similar width is obtained in the Faddeev calculations [59,60]. For a resonance mass of 2383 MeV, they obtain a width of 94 MeV for the decay into all experimentally observed
$ NN\pi\pi $ decay channels. Adding the decay width into the$ pn $ channel, which they cannot account for in their model, leads finally to a width of 104 MeV.The quark-model calculations of the IHEP group, which include hidden-color configurations, as discussed in Refs. [90,91,102], arrive at the experimentally observed width [52,82,83,103-105]. In these calculations, the
$ d^*(2380) $ hexaquark of size 0.8 fm contains approximately 67% hidden-color components, which cannot decay easily and hence reduce the width to the experimental value.The diquark model of Shi, Huang, and Wang [95] also reproduces the observed narrow width. Here, the width is naturally explained by the large tunneling suppression of a quark between a pair of diquarks. Again, Gal and Karliner [96] question this result, arguing that, in the calculation of the decay, an isospin-spin recoupling factor of 1/9 has been overlooked, which would reduce the width to less than 10 MeV. However, in a reply, Shi and Huang point out that such a recoupling factor appears only in uncorrelated quark models and not in the diquark model [94].
For completeness, we mention here also the recent work of Niskanen [106], who considers the energy balance in
$ \Delta N $ and$ \Delta\Delta $ systems. He arrives at the surprising conclusion that both these systems should have widths that are substantially smaller than the width of the free$ \Delta $ at the corresponding mass. This conclusion is not only counterintuitive, as he also notes, but also in sharp contrast to the experimental results. For example, for$ d^*(2380) $ , he obtains a width of approximately 40 MeV, and for$ D_{12} $ , a width of approximately 75 MeV, both of which are smaller than that observed experimentally. Such Fermi motion considerations have been taken up recently by Gal [107] as well for the discussion of the expected size of the$ \Delta\Delta $ configuration of$ d^*(2380) $ . In Ref. [108], it is demonstrated that such considerations lead to conflicts with the observed mass distributions. There,$\Delta {s}$ of mass 1190 MeV with a width of 80 MeV are observed, as expected from the mass-width relation of a free$ \Delta $ . This is in line with the expectation that, during the decay process$ d^*(2380) \to \Delta\Delta $ , the distance between the two$ \Delta s $ increases continuously, thus finally eliminating the Fermi motion and returning the mass and width of the$\Delta s$ to their asymptotic values. -
If the scenario of the models, which correctly reproduce the experimental width, is true, the unusually small decay width of
$ d^*(2380) $ signals indeed an exotic character of this state and points to a compact hexaquark nature of this object, as discussed by the IHEP group [82,103-105]. In fact, the IHEP calculations as well as the quark-model calculations of the Nanjing group [92] give a value as small as 0.8 - 0.9 fm for the root-mean-square radius of$ d^*(2380) $ , i.e., as small as the nucleon. Further, the latest lattice QCD calculations provide values in the same range [99]. Actually, such values appear not to be unreasonable if one uses just the uncertainty-relation formula [109]$ R \approx \hbar c / \sqrt{2\mu_{\Delta\Delta} B_{\Delta\Delta}} \approx 0.5~ {\rm fm} $

(2) for an order-of-magnitude estimate of the size of a
$ \Delta\Delta $ system bound by$ B_{\Delta\Delta} $ = 80 MeV and a reduced mass$ \mu_{\Delta\Delta} = m_{d^*(2380)} $ .In contrast, the Faddeev calculations of Gal and Garcilazo give a molecular-like
$ D_{12}-\pi $ structure with a radius of approximately 2 fm [107,110], i.e., as large as the deuteron. Unfortunately, as demonstrated recently [5,107], the$ d^* $ decay branchings into the various$ NN\pi\pi $ channels based on isospin coupling turn out to be identical for the routes$ d^* \to \Delta\Delta \to NN\pi\pi $ and$ d^* \to D_{12}\pi \to NN\pi\pi $ and hence do not discriminate between these two scenarios. Fortunately, there is a way out by looking at a possible decay into the single-pion channel. In leading order, such a decay is forbidden for$ d^* \to \Delta\Delta \to (NN\pi)_{I = 0} $ . The consideration of higher order terms yields a branching of less than 1% [58]. The situation is much different for an intermediate$ D_{12}\pi $ configuration, as$ D_{12} \to NN $ has a branching of 16% - 18% [10,21]. Hence, the$ d^* \to NN\pi $ decay should have the same branching in this scenario. However, exactly this has been excluded by the dedicated WASA single-pion production experiment [53,54]. As a consequence of this experimental result, Avraham Gal proposed a mixed scenario, where the main component of$ d^*(2380) $ consists of a compact core surrounded by a dilute cloud of$ D_{12}-\pi $ structure [107].In summary, in the present discussion about the nature of
$ d^*(2380) $ , there is no longer a question of its existence but of its structure. Is it a dilute molecular-like object or is it a compact hexaquark object? The measured decay properties of$ d^*(2380) $ clearly favor the latter. -
Stimulated by the success in establishing
$ d^*(2380) $ as the first narrow dibaryon resonance of non-trivial nature, new experiments have been conducted recently to search for other possible dibaryon resonances. With the ANKE detector at COSY, the$ pp \to pp\pi^0 $ reaction was studied with polarized protons over a large energy range$ \sqrt s $ = 2040 - 2360 MeV and under the kinematical condition that the emitted proton pair is in the relative$ ^1S_0 $ state [111]. Thus, these measurements are complementary to those of the$ pp \to d\pi^+ $ reaction, where the nucleons bound in the deuteron are in relative$ ^3S_1 $ state – aside from the small$ D $ -wave admixture in the deuteron.In the partial wave analysis of their data, the ANKE collaboration finds the
$ ^3P_0 \to $ $ ^1S_0s $ and$ ^3P_2 \to $ $ ^1S_0d $ transitions to show resonances at 2201(5) and 2197(8) MeV, respectively, with widths of 91(12) and 130(21) MeV, respectively. The resonance parameters point to$ \Delta N $ threshold states with$ I(J^P) = 1(0^-) $ and$ 1(2^-) $ , respectively, where the two constituents$ N $ and$ \Delta $ are in relative$ P $ waves. The particular signature of the$ ^3P_0 \to $ $ ^1S_0s $ and$ ^3P_2 \to $ $ ^1S_0d $ transitions is that they constitute proton spinflip transitions, which cause a concave shaped pion angular distribution, in contrast to the conventional convex shaped ones. This peculiar behavior was noted already in PROMICE/WASA [112] and COSY-TOF [113] measurements of the$ pp \to pp\pi^0 $ reaction at energies near the pion production threshold, thus providing the first hints towards a resonant behavior of these partial waves. The masses of these$ p $ -wave resonances are slightly above the nominal$ \Delta N $ mass. This is understood to be caused by the additional orbital motion [111].For the
$ I(J^P) = 1(2^-) $ resonance corresponding to the$ ^3P_2 $ $ NN $ -partial wave, a pole had been found already in SAID partial-wave analyses of data on$ pp $ elastic scattering and the$ pp \rightleftharpoons d\pi^+ $ reaction [16,21]. In these analyses, evidence for poles in$ ^3F_3 $ and$ ^3F_4- $ $ ^3H_4 $ partial waves has also been found near the$ \Delta N $ threshold, although this evidence appears much less pronounced than that for the above cases. These poles would correspond to states with$ I(J^P) = 1(3^-) $ and$ 1(4^-) $ .Kukulin and Platonova have demonstrated recently that, by accounting for the isovector
$ P $ -wave resonances, as well as the dominant isovector$ 2^+ $ resonance, the$ pp \rightleftharpoons d\pi^+ $ cross section and polarization observables can be described quantitatively for the first time with form-factor cut-off parameters, which are consistent with those obtained in elastic scattering descriptions [114].Not coupled to the
$ NN $ channel, but in the region of the$ \Delta N $ threshold, there is supposed to be another state with quantum numbers mirroring those of the$ I(J^P) = 1(2^+) $ state. This state with$ I(J^P) = 2(1^+) $ – first predicted by Dyson and Xuong in 1964 [12] and denoted by$ D_{21} $ – is decoupled from the elastic$ NN $ channel because of its isospin I = 2. Hence, it only can be produced in$ NN $ -initiated reactions associatedly, e.g., by the$ pp \to D_{21}\pi^- \to pp\pi^+\pi^- $ reaction. Although the total cross section of this two-pion production channel runs smoothly over the$ \Delta N $ threshold region, it was noted recently that its slope is not in accord with isospin relations between this channel and the$ pp \to pp\pi^0\pi^0 $ channel. The latter cannot contain a$ D_{21} $ resonance excitation owing to Bose symmetry, whereas the former can. Indeed, a detailed analysis of WASA-at-COSY$ pp \to pp\pi^+\pi^- $ data revealed pronounced differences in invariant mass spectra and angular distributions associated with$ \pi^+ $ or$ \pi^- $ . These cannot be understood by the conventional$ t $ -channel reaction mechanism; however, they can be quantitatively described by the presence of$ D_{21} $ with m = 2140(10) MeV and$ \Gamma $ = 110(10) MeV [115,116]. In addition to the prediction of Dyson and Xuong, Gal and Garcilazo obtain this state with approximately the same mass and width [60], whereas the Nanjing group does not obtain enough binding in their calculation for the formation of a bound state [117]. Yet another calculation based on hadronic interaction can produce such a bound state [118]. -
In contrast to
$ \Delta N $ resonances, which can couple solely to isovector$ NN $ channels,$ N^*N $ resonances can connect to both isoscalar and isovector$ NN $ channels. Thus, the most likely configurations, where$ N^* $ and$ N $ are in relative$ S $ -waves, can couple to$ ^1S_0 $ and$ ^3S_1 $ $ NN $ -partial waves possessing the quantum numbers$ I(J^P) = 1(0^+) $ and$ 0(1^+) $ , respectively.In fact, evidence for the existence of such states has been found just recently in
$ NN $ -initiated single- and double-pion production. In a study dedicated initially to the search for a decay$ d^*(2380) \to NN\pi $ (see section IIC.4), the isoscalar part of the single-pion production was measured in the$ d^* $ resonance region covering also the$ N^*(1440)N $ excitation region [53]. As a result, the isoscalar total cross section is observed to increase monotonically from the$ NN\pi $ threshold up to$ \sqrt s \approx $ 2.32 GeV – as is also expected for a conventional$ N^* $ excitation process mediated by$ t $ -channel meson exchange. However, one would expect in such a case that the cross section keeps rising as the beam energy is further increased. Instead, the measurements beyond 2.32 GeV exhibit a decreasing cross section, thus forming a bell-shaped energy excitation function for the isoscalar total cross section. Because the simultaneously measured isoscalar$ N\pi $ -invariant-mass distribution is in accord with an excitation of the Roper resonance$ N^*(1440) $ [53], the observation must be interpreted as evidence for a$ N^*N $ resonance [119,120]. We deal here with a state below the nominal$ N^*N $ mass of$ m_{N^*} + m_N $ = 2.38 GeV. Therefore,$ N^* $ and$ N $ must be in relative$ S $ -wave, and the quantum numbers of this resonance must be$ I(J^P) = 0(1^+) $ . That is, it is fed by the$ ^3S_1 $ partial wave in the$ NN $ -system.Because the Roper resonance also decays by emission of two pions, this
$ N^*N $ structure could be seen in isoscalar two-pion production as well. This is particularly true for the$ pn \to d\pi^0\pi^0 $ reaction, where the background of conventional processes is the lowest and$ d^*(2380) $ is observed the best. As seen in Figs. 1 and 2, there is, indeed, a small surplus of cross section in the region of$ \sqrt s \approx $ 2.3 GeV (black filled circles in Fig. 2), i.e., at the low-energy tail of the$ d^*(2380) $ resonance, which could be related to the isoscalar$ N^*N $ state.Isospin decomposition of data on various
$ pp $ -induced two-pion production channels had revealed already that the Roper$ N^*(1440) $ excitation process exhibits a bump-like structure there as well, peaking in the region of the$ N^*N $ mass [121]. Because the initial$ pp $ -system is of isovector character, the observed structure must correspond to an$ N^*N $ state with$ I(J^P) = 1(0^+) $ formed by the$ ^1S_0 $ partial wave in the initial$ pp $ channel.Both resonance structures peak around 2320 MeV and have a width of
$ \Gamma \approx $ 150 MeV. These values conform with the pole parameters of 1370 - i 88 MeV for the Roper resonance but not with its Breit-Wigner values of$ m \approx $ 1440 MeV and$ \Gamma \approx $ 350 MeV [122]. If the latter mass value is taken for the nominal$ N^*N $ mass, the two$ N^*N $ structures appear to be bound by approximately 70 MeV, which could explain that the observed width is smaller than typical for a Roper excitation. In fact, the formation of an$ N^*N $ resonance state would also explain the observation that, in nucleon-accompanied Roper excitations, such as those in hadronic$ J/\Psi \to \bar{N}N\pi $ decay [123] and$ \alpha N $ scattering [124,125], this excitation is always seen with values close to its pole parameters but not as expected with its Breit-Wigner values. -
In addition to the peak for the excitation of the
$ d^*(2380) $ resonance at$ \sqrt s $ = 2.37 GeV, two further peaks appear at 2.47 and 2.63 GeV in the total cross section of the$ \gamma d \to d\pi^0\pi^0 $ reaction, as measured recently both at ELPH [56] and at MAMI [57]. Conventionally, these two bumps are explained to belong to electromagnetic excitations of the nucleon in the second and third resonance regions [71,72], whereas the collaboration at ELPH demonstrates that the measured angular distributions are not in accord with such a quasifree reaction process but rather with a process for the formation of isoscalar dibaryon resonances with masses m = 2469(2) and 2632(3) MeV and widths$ \Gamma $ = 120(3) and 132(5) MeV, respectively [56]. No spin-parity assignments are given, but the$ d\pi $ -invariant mass spectra suggest a decay of these putative resonances via$ D_{12} $ , the isovector$ 2^+ $ state near the$ \Delta N $ threshold. The peak at 2.63 GeV is beyond the energy range measured at WASA in the$ pn \to d\pi^0\pi^0 $ reaction, whereas the peak at 2.47 GeV is still within this range. Because the peak cross section at 2.47 GeV is roughly double that for$ d^*(2380) $ at 2.37 GeV, one would naively expect a similar situation also in the hadronic excitation process measured by WASA. However, nothing spectacular is seen around 2.5 GeV in the WASA measurements. The observed small cross section in this region (see Fig. 2) is well understood by the conventional$ t $ -channel$ \Delta\Delta $ process, as indicated in Fig. 1. A possible way out could be the conception that, similar to the situation with the Roper resonance, the higher-lying nucleon excitations also undergo a kind of molecular binding with the neighboring nucleon at their threshold. Because, in$ NN $ -induced reactions, the excitation of the hit nucleon into states of the second and third resonance region has a much smaller cross section [126] than the conventional$ \Delta\Delta $ process, it could be understandable that WASA does not observe the peak at 2.47 GeV, as seen in$ \gamma $ -induced$ \pi^0\pi^0 $ production, where the$ \Delta\Delta $ process is not possible.Five out of six dibaryonic states predicted by Dyson and Xuong [12] in 1964 have been found with masses even close to the predicted ones, if the interpretation of the WASA data as evidence for
$ D_{21} $ is correct (see section VC). Therefore, it appears very intriguing to investigate whether the sixth one also exists, perhaps, close to its predicted mass value. This$ NN $ -decoupled state$ D_{30} $ with$ I(J^P) = 3(0^+) $ , i.e., with quantum numbers mirrored to those of$ D_{03} = d^*(2380) $ and of$ \Delta\Delta $ nature, is particularly difficult to find, as one needs at least two associatedly produced pions to produce it in$ NN $ -initiated reactions.An attempt to search for it in WASA data for the
$ pp \to pp\pi^+\pi^+\pi^-\pi^- $ reaction was undertaken recently [127]. No stringent signal of such a state was observed in these data, and only upper limits for its production cross section could be derived, because the theoretical description of conventional processes for four-pion production is not well known so far. However, it could be shown that the upper limit is at maximum for the combination m = 2.38 GeV and$ \Gamma $ = 100 MeV. That is, if this state really exists, this mass-width combination is the most likely one.Because this mass is compatible with the
$ d^*(2380) $ mass, it would agree perfectly with the prediction of Dyson and Xuong, who obtain equal masses for both these states. Other theoretical studies [60,80,81] also find$ D_{30} $ to lie in this mass region. -
Despite numerous experimental attempts, no single dibaryon candidate could be established firmly in the flavored quark sector so far. Most experiments were carried out in the strange sector, in particular, searching for the
$ H $ -dibaryon, a bound$ \Lambda\Lambda $ state predicted 1977 by Jaffe [128]. For a recent review see, e.g., Ref. [5]. According to very recent lattice QCD simulations close to the physical point ($ m_\pi $ = 146 MeV,$ m_K $ = 525 MeV) performed by the HAL QCD collaboration, there is no bound or resonant$ H $ -dibaryon around the$ \Lambda\Lambda $ threshold [129]. However, a possible$ H $ resonance close to the$ \Xi N $ threshold cannot yet be excluded by these calculations.The dibaryon search in the strange sector received a new push after the lattice QCD calculations by the HAL QCD collaboration kept predicting slightly bound
$ \Omega\Omega $ and$ \Omega^- p $ systems [130,131]. The latter result is also in accord with quark model calculations by the Nanjing group [132]. The first measurements of the$ \Omega^- p $ correlation function by the STAR experiment at RHIC hint that the scattering length is indeed positive, in favor of a bound state in this system [133].An established unusual structure found in the strange sector is a narrow spike at the
$ \Sigma N $ threshold, conventionally interpreted as a cusp effect [5,134-136]. However, a possible$ \Lambda N $ state has also been discussed; for a recent review on this subject, see, e.g., Ref. [137]. The question about strange partners of$d^*(2380)$ forming an antidecuplet of dibaryon states has been dealt with in Ref. [138].At JPARC, experiments are being conducted to search for a bound
$ ppK^- $ system. Recent results are in favor of the existence of such a system [139]; however, a definite confirmation is needed.Lately, particular attention has been paid to the charm and beauty sector, where tetra- and pentaquark systems were observed recently. This finding suggests that, in these sectors, the attraction is again large enough to form dibaryons. This expectation has been supported by numerous model calculations of increasing sophistication. For example, Frömel et al. [140] started out with well-established phenomenological nucleon-nucleon potentials applying quark-model scaling factors for scaling the strengths of the different interaction components and obtained first indications of deuteron-like bound states between nucleons and singly- as well as doubly-charmed hyperons. However, a quark-model investigation of doubly-heavy dibaryons does not find any bound or metastable state [141,142]. Another quark-model study finds four sharp resonance states near the
$ \Sigma_c N $ and$ \Sigma_c^* N $ thresholds [143]. A recent lattice QCD study based on the HAL QCD method [144] comes to the conclusion that the attraction in the$ \Lambda_c N $ system is not strong enough to form a bound system.Within the one-boson-exchange model, Zhu et al. have undertaken a systematic investigation of singly- and doubly-heavy baryon-baryon combinations [145-150]. They find several candidates of loosely bound molecular states in the
$ \Xi_{cc} N $ system [148], for loosely bound deuteron-like states in the$ \Xi_c\Xi_c $ and$ \Xi_c'\Xi_c' $ [145] as well as$ \Lambda_c\Lambda_c $ and$ \Lambda_b\Lambda_b $ [146] systems. They also obtain binding solutions for the$ \Xi_{cc}\Xi_{cc} $ system [147] and a pair of spin-3/2 singly-charmed baryons with the striking result that molecular states of$ \Omega_c^*\Omega_c^* $ might even be stable [149]. The possible molecular states composed of doubly charmed baryons are also investigated, and good candidates have been found, but it is also demonstrated that coupled-channel effects can be important for the question of whether there is a binding solution [150].Unfortunately, there are no experimental results yet. However, with such numerous promising candidates, it will be very interesting to see the results of future experiments in the area of charm and beauty.
-
Following a trace laid by the ABC effect, the WASA measurements of the two-pion production in
$ np $ collisions revealed the existence of a narrow dibaryon resonance, first observed in the$ pn \to d\pi^0\pi^0 $ reaction. It was found that this has been the golden channel for dibaryon discovery because the background due to conventional processes is the smallest in this channel. There was no chance to discover it via previous experiments in this channel either, as there existed no other installations that would have been able to take reliable data for this reaction channel at the energies of interest.By subsequent WASA measurements of all possible hadronic decay channels, this dibaryon state could be established as a genuine
$ s $ -channel resonance with$ I(J^P) = 0(3^+) $ at 2370 - 2380 MeV. Its dynamic decay properties point to an asymptotic$ \Delta\Delta $ configuration bound by 80 - 90 MeV. Its width of only 70 MeV – more than three times smaller than that expected for a conventional$ \Delta\Delta $ system excited by$ t $ -channel meson exchange – points to an exotic origin, such as hidden-color effects in the compact hexaquark system.Although the observation of such a state came as a surprise to many, it was predicted properly as early as in 1964 by Dyson and Xuong and more recently by Z. Y. Zhang et al., who could also reproduce all measured decay properties. Most recently, this state has also been seen in lattice QCD calculations.
Although evidence has been added for a number of dibaryonic states near the
$ \Delta N $ threshold – all of them with large widths –$ d^*(2380) $ remains the only established resonance so far with a surprisingly small width pointing to a compact hexaquark structure of this state.Key details about the (unflavored) dibaryon states discussed in this review are summarized in Table 2. For a number of them, existence is not (yet) certain. The column "evidence" provides a star rating for the presently collected experimental evidence of the envisaged state. It is based on the authors' personal judgment and may serve as a guideline. The experimentally best established one is certainly the isoscalar resonance
$ d^*(2380) $ followed by the isovector$ \Delta N $ near-threshold state with$ J^P = 2^+ $ .I $ J^P $ 

$ (^{2S+1}L_J)_{NN} $ 

m /MeV $ \Gamma $ /MeV

evidence asympt. structure experimental information theoretical calculation 0 $ 1^+ $ 

$ ^3S_1- ^3D_1 $ 

2320(10) 150(30) *** $ N^*N $ 

[119,120] [119] 0 $ 3^+ $ 

$ ^3D_3- ^3G_3 $ 

2370(10) 70(5) ***** $ \Delta\Delta$ 

[5,6,7,8,9] [12,76,78,80] $ \rightleftharpoons $ 

[11,35,36,37] [52,58,73,82] ${\rm hexaquark}$ 

[42,51,53,54] [79,84,86,88] ${\rm hidden\; color}$ 

[55,57,68,69] [89,95,96,98] [59,61,62,65] [60,100,101,107] [102,160] 0 ? ? 2469(2) 120(3) * ? [56] 0 ? ? 2632(3) 132(5) * ? [56] 1 $ 0^+ $ 

$ ^1S_0 $ 

2315(10) 150(20) * $ N^*N $ 

[119] [119] 1 $ 0^- $ 

$ ^3P_0 $ 

2201(5) 91(12) *** $ \Delta N $ 

[112] 1 $ 2^- $ 

$ ^3P_2- ^3F_2 $ 

2197(8) 130(21) **** $ \Delta N $ 

[16,21,111] [158] 1 $ 2^+ $ 

$ ^1D_2 $ 

2146(4) 118(8) **** $ \Delta N $ 

[5,16,18,19] [12,60,110,117] [158] 1 $ 3^- $ 

$ ^3F_3 $ 

2183(?) 158(?) ** $ \Delta N $ 

[16,21] [158] 1 $ 4^- $ 

$ ^3F_4- $ 

$ ^3H_4 $ 

2210(?) 156(?) * $ \Delta N $ 

[16,21] 2 $ 1^+ $ 

$ ^3P_1 + \pi $ 

2140(10) 110(10) *** $ \Delta N $ 

[115,116] [12,60,117] 3 $ 0^+ $ 

$ ^1S_0 + \pi\pi $ 

2380?? 100?? ??? $ \Delta\Delta$ 

[127] [12,60,78,80,81] Table 2. Unflavored dibaryon resonances (including candidates discussed in this review) below or near
$ \Delta(1232)N $ ,$ N^*(1440)N $ , and$ \Delta(1232)\Delta(1232) $ thresholds. The resonance states are characterized by their isospin$ I $ , spin-parity$ J^P $ , involved$ NN $ partial wave$ (^{2S+1}L_J $ with spin$ S $ , orbital angular momentum$ L $ , and total angular momentum$ J $ ), mass$ m $ , and width$ \Gamma $ . The column "evidence" shows a star rating based on the collected experimental evidence for the envisaged state (or candidate). The column "structure" denotes the asymptotic configuration of the particular state in the course of its decay into the hadronic channels or its hindrance in the case of hidden color. The column "experimental information" summarizes recent references to corresponding experimental studies. The column "theoretical calculation" lists references to theoretical studies on the particular dibaryon state.The column "structure" denotes the asymptotic configuration of the particular state in the course of its decay into the hadronic channels or its hindrance in the case of hidden color. The column "experimental information" summarizes recent references to corresponding experimental studies. The column "theoretical calculation" lists references to theoretical studies on the particular dibaryon state, providing predictions or "postdictions."
-
From the measurements of the double-pionic fusion to
$^3{\rm He}$ [33] and$^4{\rm He}$ [34], we know that$ d^*(2380) $ obviously survives in nuclear surroundings. There are several other remarkable enhancements induced by$ np $ pairs inside nuclei. One is seen in di-electron pairs [151,152] in heavy ion collisions. This may be partly due to$ d^*(2380) $ production inside nuclei [153]. Another is that the$ np $ short-range correlation is found to be approximately 20 times higher than that of$ pp $ in$ (p,p’) $ and$ (e,e’) $ scattering off nuclei [154-156]. The question arises as to whether an intermediate formation of isoscalar dibaryon states such as$ d^*(2380) $ in the course of the interaction between the nucleons in the nucleus may be an explanation for this phenomenon. This would be in line with the$ NN $ -interaction ansatz by Kukulin et al., where the short- and intermediate range part of the$ NN $ -interaction is assumed to be due to virtual$ s $ -channel dibaryon formation [157-159]. In fact, inclusion of$ d^*(2380) $ leads to a quantitative description of the$ ^3D_3 - $ $ ^3G_3 $ phase shifts in both its real and imaginary parts [160]. Similar good results are obtained for most of the partial waves with low orbital momentum when the$ NN $ -coupled dibaryon states given in Table 2 are included [119,158-160].Because
$ d^*(2380) $ appears to exist in nuclear matter, it can influence the nuclear equation of state, especially in compact stellar objects such as neutron stars. A study finds that$ d^*(2380) $ appears at densities three times the saturation density and constitutes approximately 20% of the matter in the center of neutron stars [161], depending on the assumed interaction of$ d^*(2380) $ with its surroundings [162].Moreover, because dibaryons are bosons, one may consider a Bose-Einstein condensate formed by
$ d^*(2380) $ hexaquarks. In the first study of such a scenario, it has been pointed out that stable$ d^*(2380) $ condensates could have formed in the early universe, even constituting a candidate for dark matter [163]. -
We acknowledge valuable discussions with M. Bashkanov, Stanley J. Brodsky, Y. B. Dong, A. Gal, T. Goldman, Ch. Hanhart, Fei Huang, V. Kukulin, E. Oset, M. Platonova, P. N. Shen, I. I. Strakovsky, G. J. Wagner, Fan Wang, C. Wilkin, R. Workman, and Z. Y. Zhang.
Dibaryons: Molecular versus compact hexaquarks
- Received Date: 2020-08-17
- Available Online: 2021-02-15
Abstract: Hexaquarks constitute a natural extension of complex quark systems, just as tetra- and pentaquarks do. To this end, the current status of





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF




















 DownLoad:
DownLoad: