-
Single pion photoproduction off the nucleon has been extensively studied because of its importance in determining the spectrum and properties of the nucleon resonances [1-4]. There have been many measurements of this process, accumulating a wealth of experimental data on, e.g., cross section, photon asymmetry, and target asymmetry; see, e.g., Refs. [5-9]. Based on this dataset, partial wave analyses were performed to anatomize the underlying structure of the reaction amplitude and justify the existence of the nucleon resonances theoretically. At low energies, this has been successful for exploring the photoproduction processes in chiral perturbation theory (ChPT) [10-17]. In combination with unitarization approaches [18], the valid region of the chiral amplitudes is extended, and the physical states behave as pole singularities of the unitarized amplitudes. Nevertheless, most of the unitarization methods only take the unitary cut into account, while the remaining left-hand cuts (l.h.c.s) are left out, leading to the fact that the proper analytic and crossing properties of the amplitude are not faithfully guaranteed. In consequence, spurious poles arise to mimic the contribution of the l.h.c.s, or even worse, prevent us from discovering certain truly existent poles, e.g., virtual poles, or subthreshold resonances.
In Refs. [19-21], a novel subthreshold resonance named
$ N^\ast(890) $ was found in the S$ _{11} $ wave through a prudent analysis of the covariant chiral amplitude of$ \pi N $ scattering [22-25] by applying the method of Peking University (PKU) representation [26-31]. The PKU representation respects causality and has previously been used to establish the existences of the$ \sigma $ and$ \kappa $ states [26, 28]. The discovery of the$ N^\ast(890) $ resonance is nothing but an improved implement of analyticity compared with other unitarization methods. For instance, it is pointed out in Ref. [32] that the$ N^\ast(890) $ resonance exists even in a$ K $ -matrix parametrization if a better treatment of analyticity is executed. However, it should be emphasized that, in the traditional$ K $ matrix method, without any improvement of analyticity, even if a pole emerges from the background polynomial, it is not legitimate to discuss whether it is physical or not; it only means that the non-background part of the$ K $ matrix parametrization provides incomplete characterization of the whole physics. In PKU representation, the existence of$ N^\ast(890) $ actually only depends on our understanding or knowledge of the l.h.c contribution at the qualitative level – that is, its contribution to the phase shift is negative. In this paper, we intend to explore the$ N^\ast(890) $ resonance in$ \gamma N\rightarrow \pi N $ scattering to gain more information on its properties.Our
$ \gamma N\rightarrow \pi N $ amplitudes are obtained through a dispersive representation, which is set up with the help of unitarity and analyticity [33-36]. The inputs of the dispersive representation are the$ \pi N $ final-state-interaction amplitude and the chiral tree-level$ \gamma N\rightarrow \pi N $ amplitude estimating the left hand singularities of pion photoproduction. In a single channel approximation, the former can be achieved by an Omnès solution with the$ \pi N $ scattering phase as input. The l.h.c.s are calculated based on a chiral Lagrangian with pion and nucleon fields truncated at order$ q^2 $ . We review the analytic structures of pion photoproduction amplitudes in Ref. [37] and analyze the relevant singularities that arise in our calculation. In addition, we find that the kinematic singularities in this inelastic process are rather complicated. Cuts coming from the kinematic structure depend on the organization of the analytic functions in the amplitudes. These cuts could be in the complex plane and may affect the residues of$ N^*(890) $ . To avoid such complexity, we deform these cuts in a particular way to ensure that they lie on the real axis, below the pseudo threshold of$ \pi N $ scattering.We fit the multipole amplitudes
$ E_{0+} $ (S$ _{11}pE $ and S$ _{11}nE $ ) from Ref. [38] below the$ \Delta(1232) $ peak to determine the subtraction polynomial in the dispersive representation. The residue couplings of$ N^*(890) $ can be computed by analytic continuation of the amplitude to a second sheet, in which the PKU representation of the$ \pi N $ $ {\cal{S}} $ matrix is employed. We compare the residues of$ N^*(890) $ extracted from multipole amplitudes with those of$ N^*(1535) $ obtained in Ref. [39] to determine the properties of$ N^*(890) $ and obtain structural information by analogy with the analysis of$ N^*(1535) $ .This paper is organized as follows. In Sect. II, we set up the dispersive formalism for the
$ \gamma N \to \pi N $ process. Then, the l.h.c.s are estimated based on chiral perturbation theory in Sect. III, and we also perform an analysis of the singularities that will appear in this pion photoproduction process. In the final two sections, numerical results and a summary are presented, respectively. -
The unitarity relation for the
$ \gamma N\to \pi N^\prime $ partial wave amplitude is$ \begin{aligned}[b] \frac{{\cal{M}}(s+{\rm i}\epsilon)-{\cal{M}}(s-{\rm i}\epsilon)}{2{\rm i}} =& {\rm Im}{\cal{M}}(s+{\rm i}\epsilon) \\=& {\cal{T}}^*(s+{\rm i}\epsilon)\rho(s+{\rm i}\epsilon){\cal{M}}(s+{\rm i}\epsilon)\ , \end{aligned} $

(1) where
$ {\cal{T}} $ is the pion-nucleon scattering amplitude in the$ S_{11} $ wave. The function$ \rho(s) $ is defined as$ \rho(s) = \frac{\sqrt{(s-s_{\rm L})(s-s_{\rm R})}}{s}\ , $

(2) where
$ s_{\rm R}\equiv{(m_N+m_\pi)}^2 $ and$ s_{\rm L}\equiv{(m_N-m_\pi)}^2 $ . Equivalently, Eq. (1) can be recast as$ \begin{array}{l} {\cal{M}}(s+{\rm i}\epsilon) = {\cal{S}}(s+{\rm i}\epsilon){\cal{M}}(s-{\rm i}\epsilon)\ , \end{array} $

(3) where
$ {\cal{S}}(s) = 1+2{\rm i}\rho(s){\cal{T}}(s) $ , which is the$ \pi N $ scattering$ S $ matrix in the single channel case. The scattering amplitude$ {\cal{M}} $ can be separated into two parts, i.e.,$ {\cal{M}} = {\cal{M}}_{\rm R}+{\cal{M}}_{\rm L} $ . The former part,$ {\cal{M}}_{\rm R} $ , only contains the right hand cut (RHC) starting at$ s_{\rm R} $ , while the latter part,$ {\cal{M}}_{\rm L} $ , is free of the RHC singularity. Substituting$ {\cal{M}} = {\cal{M}}_{\rm R}+{\cal{M}}_{\rm L} $ into Eq. (3), one obtains$ \begin{array}{l} {\cal{M}}_{\rm R}^+ = {\cal{S}}{\cal{M}}_{\rm R}^-+({\cal{S}}-1){\cal{M}}_{\rm L}\ . \end{array} $

(4) For convenience, the abbreviations
$ {\cal{M}}^{\pm}(s) = \underset{\epsilon\to0}{\lim}{\cal{M}}(s\pm {\rm i}\epsilon) $ have been used. To proceed, we introduce a helper function$ {\cal{D}}(s) $ , which is analytic throughout the complex$ s $ plane but encodes the same unitarity singularity as$ {\cal{M}}(s) $ . In particular, it satisfies the same unitarity condition as$ {\cal{M}}(s) $ along the unitary cut:$ \frac{{\cal{D}}^+}{{\cal{D}}^-} = \frac{{\cal{M}}^{+}}{{\cal{M}}^{-}} = {\cal{S}}\ . $

(5) By expressing the
$ {\cal{S}} $ matrix in Eq. (4) using$ {\cal{D}}(s) $ , the following relation of spectral functions can be obtained:$ \begin{array}{l} {\rm Im}\big({\cal{D}}^{-1}{\cal{M}}_{\rm R}\big) = -\big({\rm Im}{\cal{D}}^{-1}\big){\cal{M}}_{\rm L} \ . \end{array} $

(6) It is then straightforward to provide a dispersive representation for
$ {\cal{M}}_{\rm R} $ as$ {\cal{M}}_{\rm R}(s) = {\cal{D}}\left(-\frac{s^n}{\pi}\int_{s_{\rm R}}^{\infty}\frac{\big({\rm Im} {\cal{D}}^{-1}\big){\cal{M}}_{\rm L}}{s'^n(s'-s)}{\rm d} s'+{\cal{P}}\right)\ , $

(7) where
$ n $ is the number of subtractions, and$ {\cal{P}}(s) $ is a subtraction polynomial. Eventually,$ {\cal{M}}(s) = {\cal{M}}_{\rm L}+{\cal{D}}\left(-\frac{s^n}{\pi}\int_{s_{\rm R}}^{\infty}\frac{\big({\rm Im} {\cal{D}}^{-1}\big){\cal{M}}_{\rm L}}{s'^n(s'-s)}{\rm d} s'+{\cal{P}}\right)\ . $

(8) Thus, the pion photoproduction amplitude
$ {\cal{M}}(s) $ is determined up to a polynomial once$ {\cal{D}}(s) $ and$ {\cal{M}}_{\rm L}(s) $ are known.Based on the unitarity condition in Eq. (5), one can denote a spectral representation for the auxiliary function
$ {\cal{D}}(s) $ as follows:$ {\cal{D}}(s) = \frac{1}{\pi}\int_{s_R}^\infty\frac{{\cal{T}}^\ast(s)\rho(s^\prime){\cal{D}}(s^\prime)}{s^\prime-s}{\rm d}s^\prime \ . $

(9) The above representation yields an integral equation for
$ {\cal{D}}(s) $ , which has the so-called Omnés solution [40]$ {\cal{D}}(s) = \tilde{{\cal{P}}}(s)\exp\bigg[\frac{s}{\pi}\int_{s_R}^\infty\frac{\delta(s^\prime)}{s^\prime(s^\prime-s)}{\rm d}s^\prime\bigg], $

(10) where
$ \tilde{{\cal{P}}} $ stands for zero points in the complex plane, and$ \delta(s) $ is the elastic$ \pi N $ phase shift, in accordance with the Watson final state interaction (FSI) theorem [41]. -
Single one-pion photoproduction off the nucleon (
$ \gamma N $ -$ 1\pi $ ) is the process described by$ \begin{array}{l} \gamma(q)+N(p)\to \pi^a(q^\prime)+N^\prime(p^\prime)\ , \end{array} $

(11) where
$ a $ is the isospin index of the pion, and the momenta of the particles are indicated in parentheses. The isospin structure of the scattering amplitude can be written as$ \begin{aligned}[b] {\cal{M}}(\gamma+N\to \pi^a+N^\prime) =& \chi_N^\prime \bigg \{ \delta_{a3}\,{\cal{M}}^+\\&+\frac{1}{2}[\tau_a,\tau_3]\,{\cal{M}}^-+\tau_3\,{\cal{M}}^0\bigg \} \chi_N \ , \end{aligned} $

(12) where
$ \tau_a $ ($ a = 1,2,3 $ ) are Pauli matrices in isospin space. Amplitudes with definite isospin$ I = \frac{1}{2},\frac{3}{2} $ can be obtained from$ {\cal{M}}^{\pm} $ and$ {\cal{M}}^0 $ via① ②$ {\cal{M}}^{I = \frac{3}{2}} = \sqrt{\frac{2}{3}}\left({\cal{M}}^{+}-{\cal{M}}^{-}\right)\ , $

(13) $ {\cal{M}}^{I = \frac{1}{2}} = -\frac{1}{\sqrt{3}}\left({\cal{M}}^{+}+2{\cal{M}}^{-}+3{\cal{M}}^{0}\right)\ , \ {(p\; {\rm{target}})} $

(14) $ {\cal{M}}^{I = \frac{1}{2}} = \frac{1}{\sqrt{3}}\left({\cal{M}}^{+}+2{\cal{M}}^{-}-3{\cal{M}}^{0}\right) \ , \ {(n\; {\rm{target}})}\ . $

(15) The isospin amplitudes
$ {\cal{M}}^{I} $ with either$ I = \frac{1}{2},\frac{3}{2} $ or$ I = \pm,0 $ can be further decomposed in terms of four independent Lorentz operators as follows,$ \begin{aligned}[b] {\cal{M}}^{I}(s,t)\equiv& \bar{u}(p^\prime){\cal{T}}^{I}u(p)\\=& \bar{u}(p^\prime)\bigg[\displaystyle\sum\limits_{i = 1}^{4}{\cal{A}}_i^{I}(s,t)\,{L}^i_\mu \epsilon^\mu \bigg]u(p)\ , \end{aligned}$

(16) where
$ \begin{aligned}[b] L^1_{\mu} =& {\rm i}\gamma_5\gamma_{\mu}\gamma\cdot q\ , \\ L^2_{\mu} =& 2{\rm i}\gamma_5\left(P_{\mu}q\cdot q'-q'_{\mu}P\cdot q\right)\ , \\ L^2_{\mu} =& \gamma_5\left(\gamma_{\mu}q'\cdot q-q'_{\mu}\gamma\cdot q\right)\ , \\ L^4_{\mu} =& 2\gamma_5\left(\gamma_{\mu}P\cdot q-P_{\mu}\gamma\cdot q\right)\ . \end{aligned} $

(17) Note that the operators
$ L^i_\mu $ obey the Ward identity [1]. Here,$ \epsilon_\mu $ is the polarization vector of the photon, and$ u(p) $ and$ \bar{u}(p^\prime) $ are the spinors of the nucleons. -
The effective Lagrangian for our calculation of the chiral amplitude up to
$ {\cal{O}}(p^2) $ reads$ \begin{array}{l} {\cal{L}}_{\rm eff} = {\cal{L}}_{\pi N}^{(1)}+{\cal{L}}_{\pi N}^{(2)}+{\cal{L}}_{\pi \pi}^{(2)}, \end{array} $

(18) with the superscripts referring to chiral orders. The terms in the above equation are given by [42]
$ {\cal{L}}_{\pi N}^{(1)} = \bar{\Psi}\left({\rm i}{\not \!\! D }-m+\frac{g}{2}\gamma^{\mu}\gamma_5u_{\mu}\right)\Psi \ , $

(19) $ \begin{aligned}[b] {\cal{L}}_{\pi N}^{(2)} =& \bar{\Psi}\sigma^{\mu\nu}\left[\frac{c_6}{2}f^+_{\mu\nu}+\frac{c_7}{2}v_{s,\mu\nu}\right]\Psi\ , \\ {\cal{L}}_{\pi\pi}^{(2)} =& \frac{F^2}{4}{\rm Tr}\left[D_{\mu}U{\left(D^{\mu}U\right)}^{\dagger}\right]+\frac{F^2}{4}{\rm Tr}\left(\chi U^{\dagger}+U\chi^{\dagger}\right)\ , \end{aligned} $

(20) where
$ m $ ,$ g $ , and$ F $ are the nucleon mass, nucleon axial coupling, and pion decay constant in the chiral limit, respectively. Given our working accuracy, they are set equal to their physical counterparts,$ m_N $ ,$ g_A $ , and$ F_\pi $ , i.e., the physical nucleon mass, physical axial charge, and pion decay constant, respectively. Specifically,$ m = m_N $ ,$ g = g_A $ , and$ F = F_\pi $ . Here,$ c_{6} $ and$ c_7 $ are$ {\cal{O}}(p^2) $ low energy constants (LECs), which are known parameters to be determined by experimental data; see Ref. [42] for definitions of the chiral blocks.The relevant pieces extracted from the expanded form of the Lagrangians in Eq. (19) are
$ \begin{aligned}[b] {\cal{L}}^{(1)}_{\pi N}\supset\,+&\frac{g_A}{2F_{\pi}}\partial_{\mu}\phi\bar{\Psi}\gamma_5\gamma^{\mu}\Psi -\frac{e}{2}A_{\mu}\bar{\Psi}\left[\gamma^{\mu}\left(\tau_3+1\right)\right]\Psi \\-&{\rm i}\frac{eg_A}{4F_{\pi}}A_{\mu}\bar{\Psi}\left(\gamma_5\gamma^{\mu}\left[\phi,\tau_3\right]\right)\Psi\ , \end{aligned} $

(21) $\begin{aligned}[b] {\cal{L}}^{(2)}_{\pi N}\supset\,-e\bar{\Psi}\sigma^{\mu\nu}\left[\frac{c_6}{2}\left(\partial_{\mu}A_{\nu}-\partial_{\nu}A_{\mu}\right)\tau_3+\frac{c_7}{4}\left(\partial_{\mu}A_{\nu}-\partial_{\nu}A_{\mu}\right)\right]\Psi\ , \end{aligned} $

(22) $ {\cal{L}}_{\pi\pi}^{(2)}\supset-\frac{{\rm i}e}{8}A^{\mu}{\rm Tr}\left( \left \{ \partial_{\mu}\phi,\left[\phi,\tau_3\right] \right \} \right)\ . $

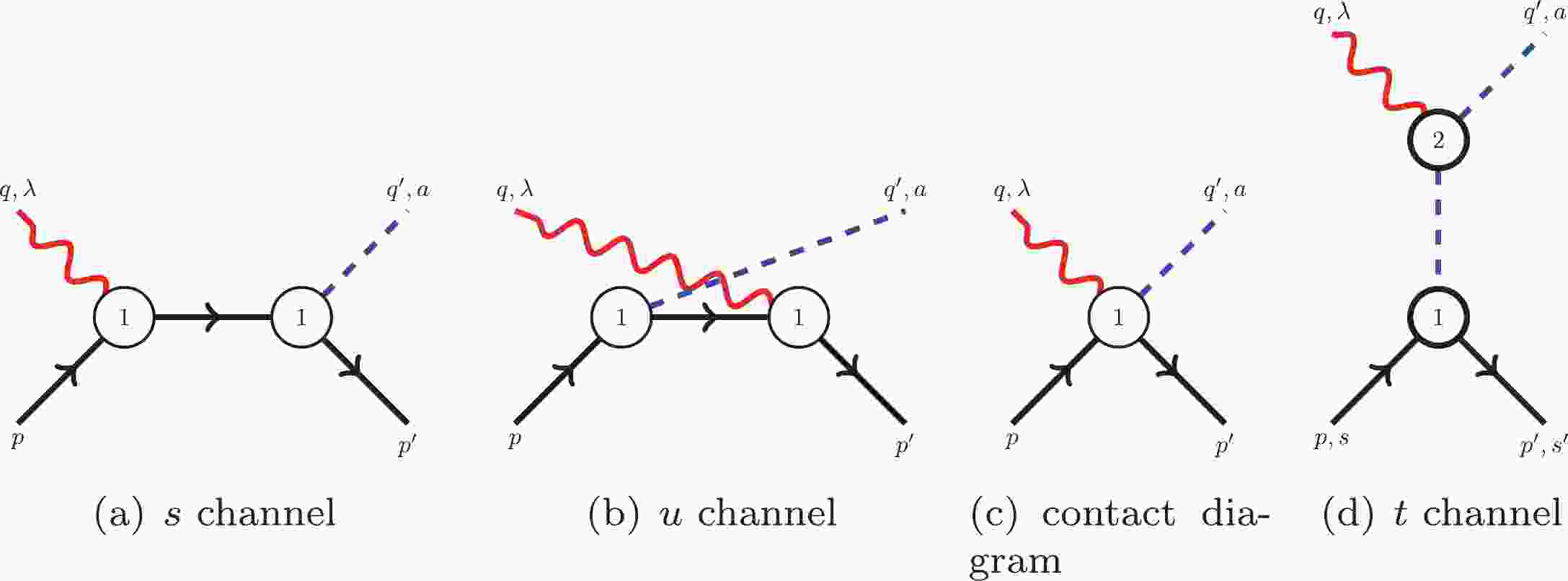
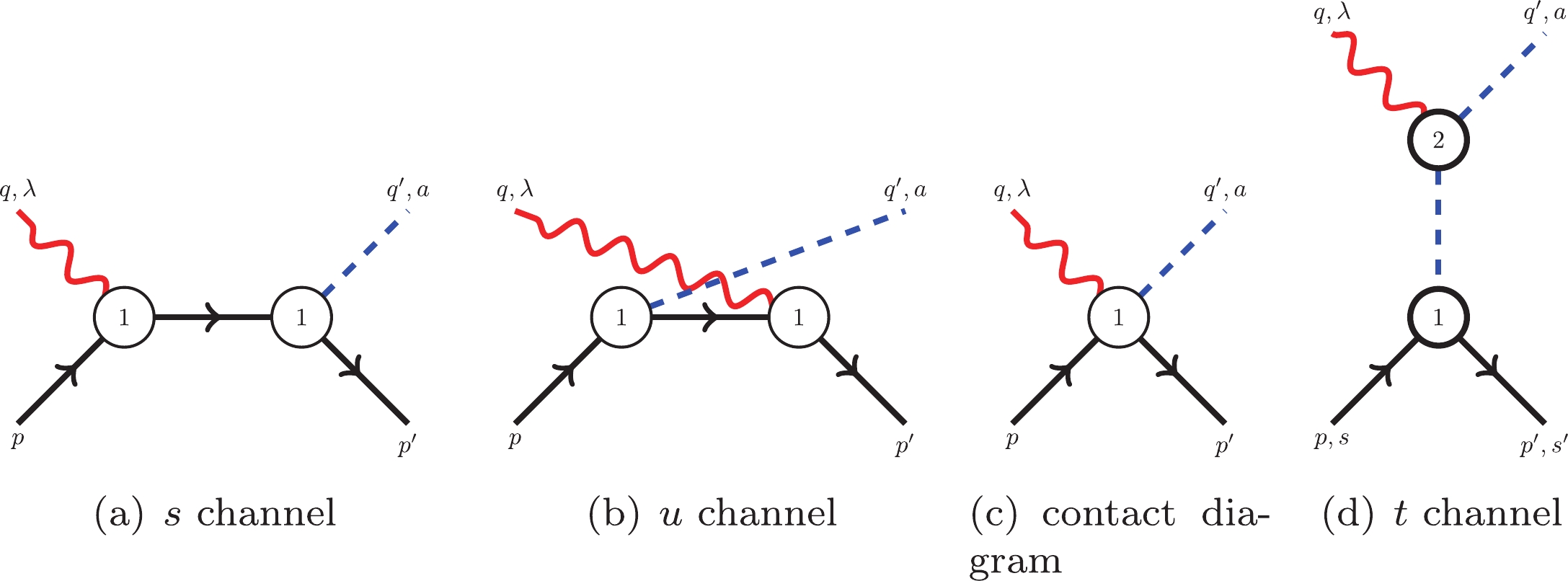
(23) Tree-level Feynman diagrams up to
$ {\cal{O}}(q^2) $ are displayed in Figs. 1 and 2.The full amplitude is
$ \begin{aligned}[b] {\rm i}{\cal{M}}^{(1)} =& \frac{eg_A}{4F_{\pi}}\chi^{\dagger}_f\left[\tau_a,\tau_3\right]\chi_i\bar{u}_{s'}(p')\gamma_5\gamma^{\mu}u_s(p)\epsilon_{\lambda,\mu}(q) \\& +\frac{{\rm i}eg_A}{4F_{\pi}}\chi^{\dagger}_f\tau_a\left(\tau_3+1\right)\chi_i\bar{u}_{s'}(p')\gamma_5\gamma^{\nu}\frac{\rm i}{{\not \!\!p }+{\not \!\!q }-m_N+{\rm i}\epsilon}\gamma^{\mu}u_s(p)q'_{\nu}\epsilon_{\lambda,\mu}(q) \\& +\frac{{\rm i}eg_A}{4F_{\pi}}\chi^{\dagger}_f\left(\tau_3+1\right)\tau_a\chi_i\bar{u}_{s'}(p')\gamma^{\mu}\frac{\rm i}{{\not\!\! p }'-{\not\!\!q }-m_N+{\rm i}\epsilon}\gamma_5\gamma^{\nu}u_s(p)q'_{\nu}\epsilon_{\lambda,\mu}(q) \\& -\frac{{\rm i}eg_{A}}{4F_{\pi}}\chi_f^{\dagger}\left[\tau_a,\tau_3\right]\chi_i\epsilon^{\nu}_{\lambda}(q)q'_{\nu}\bar{u}_{s'}(p')\gamma_5\gamma^{\mu}u_s(p)\frac{{\rm i}\left(p'_{\mu}-p_{\mu}\right)}{{\left(p'-p\right)}^2-m_{\pi}^2+{\rm i}\epsilon} \\ & +\frac{{\rm i}eg_A}{4F_{\pi}}\chi_f^{\dagger}\left[\tau_a,\tau_3\right]\chi_i\epsilon^{\nu}_{\lambda}(q)\bar{u}_{s'}(p')\gamma_5\gamma^{\mu}u_s(p)\frac{{\rm i}\left(p'_{\nu}-p_{\nu}\right)\left(p'_{\mu}-p_{\mu}\right)}{{\left(p'-p\right)}^2-m_{\pi}^2+{\rm i}\epsilon}\ , \end{aligned} $

(24) $ \begin{aligned}[b] {\rm i}{\cal{M}}^{(2)} =& \frac{-eg_A}{2F_{\pi}}\chi_f^{\dagger}\tau_a\bigg[\frac{c_6}{2}\left(q_{\nu}\epsilon_{\mu,\lambda}(q)-q_{\mu}\epsilon_{\nu,\lambda}(q)\right)\tau_3 \\& +\frac{c_7}{4}\left(q_{\nu}\epsilon_{\mu,\lambda}(q)-q_{\mu}\epsilon_{\nu,\lambda}(q)\right)\bigg]\chi_i{q'}^{\rho}\bar{u}_{s'}(p')\gamma_5\gamma_{\rho}\frac{\rm i}{\left({\not \!\!q }+{\not\!\! p }\right)-m_N+{\rm i}\epsilon}\sigma^{\mu\nu}u_s(p) \\ & +\frac{-eg_A}{2F_{\pi}}\chi_f^{\dagger}\bigg[\frac{c_6}{2}\left(q_{\nu}\epsilon_{\mu,\lambda}(q)-q_{\mu}\epsilon_{\nu,\lambda}(q)\right)\tau_3 \\& +\frac{c_7}{4}\left(q_{\nu}\epsilon_{\mu,\lambda}(q)-q_{\mu}\epsilon_{\nu,\lambda}(q)\right)\bigg]\tau_a\chi_i{q'}^{\rho}\bar{u}_{s'}(p')\sigma^{\mu\nu}\frac{\rm i}{\left({\not \!\!p }-{\not \!\!q }'\right)-m_N+{\rm i}\epsilon}\gamma_5\gamma_{\rho}u_s(p)\ , \end{aligned} $

(25) where the superscript stands for chiral order. Now, the invariant scalar functions can be extracted from the above amplitudes:
$ \begin{aligned}[b] {\cal{A}}_1^{+} =& -\frac{{\rm i}eg_A{m}_N}{2F_{\pi}}\left(\frac{1}{u-m_N^2}+\frac{1}{s-m_N^2}\right)\\&-\frac{{\rm i}eg_A{c}_6}{F}\left(\frac{2m_N^2}{u-m_N^2}+\frac{2m_N^2}{s-m_N^2}+1\right)\ , \\ {\cal{A}}_1^{0} =& -\frac{{\rm i}eg_A{m}_N}{2F_{\pi}}\left(\frac{1}{u-m_N^2}+\frac{1}{s-m_N^2}\right)\\&-\frac{{\rm i}eg_A{c}_7}{2F}\left(\frac{2m_N^2}{u-m_N^2}+\frac{2m_N^2}{s-m_N^2}+1\right)\ , \\ {\cal{A}}_1^{-} =& -\frac{{\rm i}eg_A{m}_N}{2F_{\pi}}\left(-\frac{1}{u-m_N^2}+\frac{1}{s-m_N^2}\right)\\&-\frac{{\rm i}eg_A{c}_6}{F}\left(-\frac{2m_N^2}{u-m_N^2}+\frac{2m_N^2}{s-m_N^2}\right)\ , \\ {\cal{A}}_2^{+} =& \frac{{\rm i}eg_A{m}_N}{4F_{\pi}P\cdot q}\left(\frac{1}{u-m_N^2}-\frac{1}{s-m_N^2}\right)\ , \end{aligned} $

(26) $ \begin{aligned}[b] {\cal{A}}_2^{0} =& \frac{{\rm i}eg_A{m}_N}{4F_{\pi}P\cdot q}\left(\frac{1}{u-m_N^2}-\frac{1}{s-m_N^2}\right)\ , \\ {\cal{A}}_2^{-} =& -\frac{{\rm i}eg_A{m}_N}{4F_{\pi}P\cdot q}\left(\frac{1}{u-m_N^2}+\frac{1}{s-m_N^2}+\frac{4}{t-m_{\pi}^2}\right)\ , \\ {\cal{A}}_3^{+} =& \frac{eg_A{c}_6m_N}{F_{\pi}}\left(\frac{1}{u-m_N^2}-\frac{1}{s-m_N^2}\right)\ , \\ {\cal{A}}_3^{0} =& \frac{eg_A{c}_7m_N}{2F_{\pi}}\left(\frac{1}{u-m_N^2}-\frac{1}{s-m_N^2}\right)\ , \\ {\cal{A}}_3^{-} =& \frac{eg_A{c}_6m_N}{F_{\pi}}\left(-\frac{1}{u-m_N^2}-\frac{1}{s-m_N^2}\right)\ , \\ {\cal{A}}_4^{+} =& -\frac{eg_A{c}_6m_N}{F_{\pi}}\left(\frac{1}{u-m_N^2}+\frac{1}{s-m_N^2}\right)\ , \\ {\cal{A}}_4^{0} =& -\frac{eg_A{c}_7m_N}{2F_{\pi}}\left(\frac{1}{u-m_N^2}+\frac{1}{s-m_N^2}\right)\ , \\ {\cal{A}}_4^{-} =& -\frac{eg_A{c}_6m_N}{F_{\pi}}\left(-\frac{1}{u-m_N^2}+\frac{1}{s-m_N^2}\right)\ \ . \end{aligned} $

-
It is convenient to perform partial wave projection using the helicity formalism proposed in Ref. [43]. To that end, the photon polarization vector
$ \epsilon_\mu(q) $ and the nucleon spinors$ u(p) $ and$ \bar{u}(p^\prime) $ in Eq. (16) can be substituted by their helicity eigenstates$ \epsilon_\mu(q,\lambda_2) $ ,$ u(p,\lambda_1) $ , and$ \bar{u}(p^\prime,\lambda_3) $ in the center of mass frame③, where$ \lambda_i $ ($ i = 1,2,3 $ ) values are the helicity quantum numbers of the initial nucleon, photon, and final nucleon, respectively. For each set of helicity quantum numbers, denoted as$ H_s\equiv \{\lambda_1\lambda_2\lambda_3\} $ , there is a helicity amplitude$ {\cal{M}}^I_{H_s} $ , which can be expanded as④$ {\cal{M}}_{H_s}^I(s,t) = 16\pi\sum\limits_{J = M}^\infty(2J+1){\cal{M}}_{H_s}^{IJ}(s)\,{d}_{\lambda\lambda^\prime}^J(\theta)\ , $

(27) where
$ M = \lambda $ ,$ \lambda\equiv\lambda_1-\lambda_2 $ , and$ \lambda^\prime\equiv\lambda_3 $ .$ d^J(\theta) $ is the standard Wigner$ d $ -function. By imposing the orthonormal properties of the$ d^J $ functions, the partial wave helicity amplitudes$ {\cal{M}}_{H_s}^{IJ}(s) $ in the above equation can be projected, i.e.,$ {\cal{M}}^{IJ}_{H_s}(s) = \frac{1}{32\pi}\int_{-1}^{1} {\rm d}\cos\theta {\cal{M}}^{I}_{H_s}(s,t) d_{\lambda,\lambda'}^{J}(\theta)\ . $

(28) The partial wave amplitude with
$ I = \frac{1}{2} $ ,$ J = \frac{1}{2} $ , and$ L = 0 $ (denoted by S$ _{11} $ in the$ L_{2I2J} $ convention) is obtained via$ \begin{array}{l} {\cal{M}}(S_{11}) = \bigg({\cal{M}}^{I = \frac{1}{2}J = \frac{1}{2}}_{+++}+{\cal{M}}^{I = \frac{1}{2}J = \frac{1}{2}}_{++-}\bigg)\ , \end{array} $

(29) which carries certain parity⑤, and the helicity indices
$ \lambda_i = \pm\frac{1}{2} $ or$ \pm 1 $ are abbreviated as$ \pm $ . -
To illustrate the analytic structure of the partial wave amplitudes, we rewrite the partial wave projection formula in Eq. (28) in the following form,
$ {\cal{M}}^{IJ}_{H_s}(s) = \frac{1}{32\pi}\int_{t_{\min}}^{t_{\max}} \sum_{i = 1}^4\big[{({\cal{G}}_{H_s}^J)}_i{\cal{A}}_i^I(s,t)\big]{\rm d}t\ , $

(30) where the invariant amplitude
$ {\cal{M}}^I_{H_s} $ has been replaced by its Lorentz-decomposed expression given in Eq. (16), and$ t_{\min},\ t_{\max} $ correspond to$ \cos{\theta} = \pm 1 $ through Eq. (32). Furthermore, the scalar functions$ {({\cal{G}}_{H_s}^{J})}_i $ ($ i = 1,\cdots 4 $ ) are defined by$ {({\cal{G}}_{H_s}^{J})}_i\equiv\bar{u}L^{i}_{\mu}u\epsilon^\mu\frac{d^J_{\lambda_1\lambda^\prime}(s,t)}{s\rho_{\pi N}\rho_{\gamma N}}\ , $

(31) where
$ L^{i}_{\mu} $ can be found in Eq. (17). In what follows, we proceed to discuss the analytic structure with the help of Eq. (30). Note here that the Mandelstam variable$ t $ is related to the cosine of the scattering angle$ \theta $ via$ t = 2m_N^2-\frac{\left(s+m_N^2\right)\left(s+m_N^2-m_{\pi}^2\right)}{2s}+s\rho_{\pi N}\rho_{\gamma N}\frac{\cos\theta}{2}\ . $

(32) On the one hand, it should be emphasized that the functions
$ {({\cal{G}}_{H_s}^{J})}_{i = \ldots ts,4} $ rely merely on the kinematic structures of the scattering amplitudes, regardless of the dynamics of the system under consideration. Therefore, they are model-independent and can be calculated straightforwardly for any partial wave quantum number of$ J $ . In Appendix A, for$ J = {1}/{2} $ and$ H_s $ = {++–,+++}, all the explicit expressions of$ {({\cal{G}}_{H_s}^{J})}_{i} $ are listed for the sake of easy reference. It can be observed that$ {({\cal{G}}_{H_s}^{J = \frac{1}{2}})}_{i} $ in the S$ _{11} $ channel are simply polynomials of$ t $ .On the other hand, information about the dynamics is completely encoded in the scalar amplitudes
$ {\cal{A}}^I_{i}(s,t) $ . In our tree-level ChPT calculation, they are represented by the results shown in subsection III.B, which are composed of contact terms, the$ t $ -channel pion-pole, and$ s $ - and$ u $ -channel nucleon-exchange contributions. The contact term and$ s $ -channel nucleon exchange term are polynomials of$ t $ , while the$ t $ - and$ u $ -channel pole terms⑥ can be unified to a single type,$ 1/(t-c) $ , with$ c $ a function of$ s $ .Restricted to our tree-level calculation and with the above discussions, one can conclude that there exists only one master integral:
$ \int_{t_{\min}}^{t_{\max}}\frac{t}{t-c}{\rm d}t = t_{\max}-t_{\min}+c\left[{\ln}\left(t_{\max}-c\right)-{\ln}\left(t_{\min}-c\right)\right]\ . $

(33) All other integrals are either trivial in the sense that they are integrations over polynomials of
$ t $ , able to be reduced to the above integral by making use of the identity$ \dfrac{t^n}{t-c} = t^{n-1}+\dfrac{ct^{n-1}}{t-c} $ , where$ n $ is a positive integer. In our current case, the constant$ c $ has three options, i.e.,$ c\in \{m_\pi^2, s-m_N^2-m_\pi^2, 2s-2m_N^2-m_\pi^2\} $ , which result in three typical logarithms$ {\cal{D}}_i(s) $ after applying Eq. (33); we refer the readers to Appendix 6 for their explicit expressions. For$ {\cal{D}}_i(s) $ , except$ {\cal{D}}_3(s) $ , which comes from kinematic decomposition, it should be mentioned that these logarithms stem from the dynamics term$ 1/(t-c) $ , while their composite arguments could be square root functions originating from the kinematic limits of the integrations. The logarithms and square root functions give rise to the partial-wave singularities discussed in the following subsections. -
The generic dynamic singularities of the partial-wave photoproduction amplitude have been discussed in detail in Ref. [37]. All possible singularities are displayed in Fig. 3 and are briefly illustrated as follows:
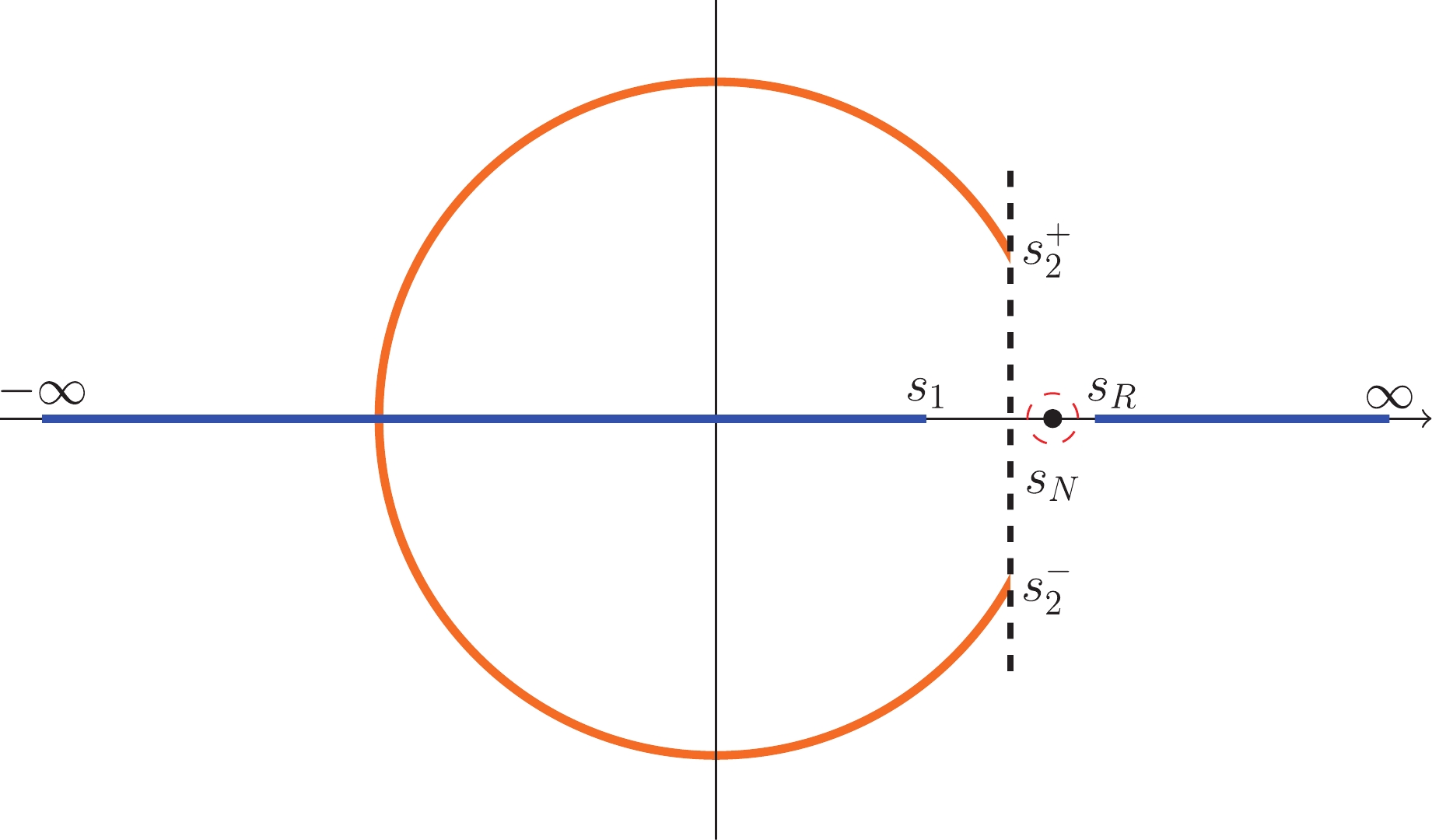
Figure 3. (color online) Dynamic singularities.
$ s_N = m_N^2 $ ,$s_1 = \dfrac{m_N}{m_{\pi}+m_N}\left(m_N^2-m_N{m}_{\pi}-m_{\pi}^2\right).$ ● unitarity cut:
$ s\in[s_{\rm R},\infty) $ on account of the$ s $ -channel continuous spectrum.●
$ u $ -channel crossed cut:$ s\in(-\infty,s_1] $ with$ s_1 = \dfrac{m_N}{m_{\pi}+m_N}\left(m_N^2-m_N{m}_{\pi}-m_{\pi}^2\right) $ due to the$ u $ -channel continuous spectrum for$ {u\geq(m_N+m_\pi)}^2 $ .●
$ t $ -channel crossed cut: I. The arc, with branch points located at$ s_2^\pm = m_N^2-\frac{3}{2}m_{\pi}^2\pm\frac{\rm i}{2} m_{\pi } \sqrt{\frac{44}{5}m_N^2-9 m_{\pi }^2} $ , stems from the$ t $ -channel continuous spectrum for$ 4m_{\pi}^2\leqslant t \leqslant 4m_N^2 $ . ⑦ II. The$ t $ -channel continuous spectrum above$ 4m_N^2 $ yields the cut$ s\in(-\infty,0] $ .● Trivial cut:
$ s\in(-\infty,0] $ generated by the logarithms.● Discrete term: located at
$ s = m_N^2\equiv s_N $ and induced by the$ t $ -channel single pion exchange as well as the$ u $ -channel single nucleon exchange⑧.Let us return to our special case under consideration. Because the continuous spectra are absent for a tree-level calculation, we meet only with the dynamic singularities of the trivial cut and the discrete term.
-
Aside from the above-mentioned dynamic singularities, there exist additional kinematic singularities for an inelastic scattering process with spinors. The kinematic singularities are caused by the square-root and/or logarithmic functions appearing in the partial wave amplitudes. Kinematic cuts are introduced when the arguments of those two kinds of functions are negative. All the involved arguments, together with their corresponding negative domains, are listed in Table 1.
arguments negative domain $ s-s_{\rm R} $ 

$ \left(-\infty,s_{\rm R}\right) $ 

$ s-s_{\rm L} $ 

$ \left(-\infty,s_{\rm L}\right) $ 

$ s $ 

$ \left(-\infty,0\right) $ 

$ s+m_N^2-m_{\pi}^2-\sqrt{s-s_{\rm R}}\sqrt{s-s_{\rm L}} $ 

- $ s+m_N^2-m_{\pi}^2+\sqrt{s-s_{\rm R}}\sqrt{s-s_{\rm L}} $ 

$ \left(-\infty,0\right) $ 

$ 3s+m_N^2-m_{\pi}^2-\sqrt{s-s_{\rm R}}\sqrt{s-s_{\rm L}} $ 

$ \left(-\infty,\frac{1}{2}\left(m_{\pi}^2-2m_N^2\right)\right) $ 

$ 3s+m_N^2-m_{\pi}^2+\sqrt{s-s_{\rm R}}\sqrt{s-s_{\rm L}} $ 

$ \left(-\infty,0\right) $ 

$ s-m_N^2+m_{\pi}^2-\sqrt{s-s_{\rm R}}\sqrt{s-s_{\rm L}} $ 

$ \left(0,s_{\rm L}\right) $ 

$ s-m_N^2+m_{\pi}^2+\sqrt{s-s_{\rm R}}\sqrt{s-s_{\rm L}} $ 

$ \left(-\infty,s_{\rm L}\right) $ 

Table 1. Arguments causing singularities.
It should be pointed out that these functions are organized in a way that does not affect the value in the physical region, but may affect the values in the complex plane. Here, we give an example to illustrate this point:
$ \sqrt{\left(s-s_{\rm R}\right)\left(s-s_{\rm L}\right)} $ Case: There are two cuts. One goes from$ s_{\rm L} $ to$ s_{\rm R} $ , and the other is an infinitely-long line, which is perpendicular to the real axis and passes the midpoint of$ s_{\rm L} $ and$ s_{\rm R} $ .$ \sqrt{s-s_{\rm R}}\sqrt{s-s_{\rm L}} $ Case: There is just one cut, stretching from$ s_{\rm L} $ to$ s_{\rm R} $ , with the cuts below$ s_{\rm L} $ cancelling each other out.Meanwhile, the values in the physical region in the above two cases are the same. In practice, we choose to expand the root functions in terms of power series and then continue them to the full complex plane. In this way, all the kinematic singularities represent themselves as cuts lying on the real axis, and the logarithm functions in the form of
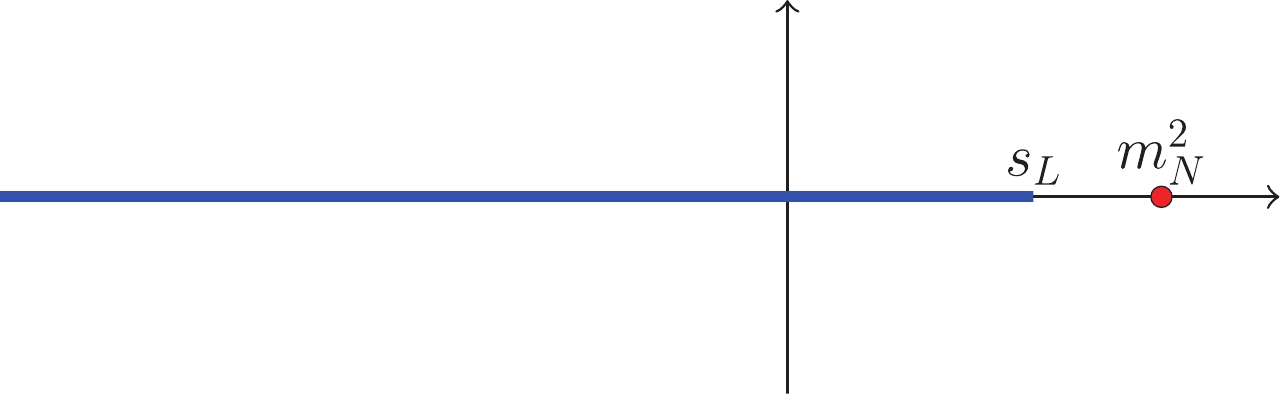
$ \ln\dfrac{a}{b} $ , whose arguments contain root functions, are recast to$ {\ln}a-{\ln}b $ to avoid a circular cut in the complex plane.For the S
$ _{11} $ channel, the cut between$ s_{\rm L} $ and$ s_{\rm R} $ disappears because$ {\cal{M}}^{I = \frac{1}{2}J = \frac{1}{2}}_{+++} $ and$ {\cal{M}}^{I = \frac{1}{2}J = \frac{1}{2}}_{++-} $ are conjugated with each other in this interval; this is easy to understand in light of the explicit form of$ {({\cal{G}}_{H_s}^{J})}_i $ given in Appendix A. In addition, there is a pole-like singularity at$ m_N^2 $ coming from the fact that$ \lim_{s\to m_N^2}\dfrac{{\cal{D}}_i}{\rho_{\gamma-N}} $ , where the source of$ \frac{1}{\rho} $ can be seen in Eq. (30), diverges; meanwhile, the limit of$ \lim_{s\to s_{\rm R}}\dfrac{{\cal{D}}_i}{\rho_{\gamma-N}} $ is finite. However, the apperance of this pole-like singularity in the amplitude can be viewed as the branch point of the l.h.c starting from$ m_N^2 $ in the$ {\cal{S}} $ matrix because$ S_{\gamma\pi} = \sqrt{\rho_{\gamma N}\rho_{\pi N}}T $ , where$ S_{\gamma\pi} $ is the pion photoproduction$ {\cal{S}} $ matrix, or the branch point of the electromagnetic unitarity cut of amplitudes. The results for an additional singularity in the$ S_{11} $ channel are displayed in Fig. 4.As a result of kinematic singularities, we should include
$ s $ -channel and contact diagrams in addition to$ t $ - and$ u $ -channel resonance exchanges in the estimation of$ {\cal{M}}_{\rm L} $ at tree level. -
We are now in the position to compare the dispersive representation of the photoproduction amplitude given in Eq. (8) with experimental multipole amplitude data from Ref. [38] in the
$ S_{11} $ channel. Based on our fitting results, the couplings of$ N^\ast(890) $ to$ \gamma N $ and$ \pi N $ can be extracted. -
There are three different kinds of parameters in Eq. (8): the LECs involved in determination of
$ {\cal{M}}_{\rm L}(s) $ , the subtraction constants in the auxiliary function$ {\cal{D}}(s) $ , and the parameters in the overall subtraction polynomial$ {\cal{P}}(s) $ . First, the parameters in the Lagrangian appearing in$ {\cal{M}}_{\rm L}(s) $ are chosen to be$ m_N =$ $ 938.3\; {\rm MeV} $ ,$ m_{\pi} = 139.6\; {\rm MeV} $ ,$ e = 0.303 $ ,$ g_A = 1.267 $ ,$ F_{\pi} = 92.4\; {\rm MeV} $ ,$ c_6 = {3.706}/{(4m_N)} $ , and$ c_7 = {-0.12}/{(2m_N)} $ [44]⑨. Second, we set$ \tilde{{\cal{P}}}(s) = 1 $ and compute$ {\cal{D}}(s) $ using the$ S_{11} $ -wave phase shift extracted from the$ \pi N $ $ S $ matrix given in Ref. [19]. Two solutions of the$ \pi N $ $ S $ matrix are adopted: one corresponding to$ s_c = -1\; \rm{GeV}^2 $ , and the other to$ s_c = -9\; \rm{GeV}^2 $ , with$ s_c $ being a cut off parameter therein. Note that it should be a good approximation for a single-channel case that the integrations in Eqs. (10) and (8) are performed up to$ 2.095\;\rm GeV^2 $ , rather than to infinity. Finally, the constants in$ {\cal{P}} $ are left as fitting parameters.⑩ Here, we only consider two fit cases: Fit I with$ {\cal{P}}(s) = a $ and Fit II with$ {\cal{P}}(s) = a+b\, s $ , while the subtraction points are set to zero.We perform a fit to the data points on the multipole amplitudes⑪, which are traditionally denoted by S
$ _{11} $ with suffixes of target type (n or p) and electromagnetic transition ($ E $ : electric,$ M $ : magnetic), from the$ \pi N $ threshold to$ 1.440\; \rm GeV^2 $ , which is just below the peak of$ \Delta(1232) $ . The fit results for both proton (p) and neutron (n) targets are displayed in Figs. 5 and 6, respectively. For comparison, in Fig. 5 and Fig. 6, we also show the$ {\cal{O}}(q^2) $ chiral results of the real parts of the multipole amplitudes. As expected, the chiral results only describe the data very well at low energies close to threshold. The values of the fit parameters are presented in Table 2.target case parameter value $ \chi^2/d.o.f $ 

p Fit I $ 10^2\times a $ 

$ -0.0712\pm0.1334 $ 

$ 1.58 $ 

Fit II $ 10^2\times a $ 

$ 0.0287\pm3.2525 $ 

$ 1.63 $ 

$ 10^2\times b $ 

$ -0.210\pm2.504 $ 

n Fit I $ 10^2\times a $ 

$ -1.43\pm0.35 $ 

$ 1.22 $ 

Fit II $ 10^2\times a $ 

$ 12.50\pm6.90 $ 

$ 0.643 $ 

$ 10^2\times b $ 

$ -10.4\pm5.2 $ 

Table 2. Results of the fit parameters.
$ a $ is dimensionless, and the unit of$ b $ is$ \rm{GeV}^{-1} $ .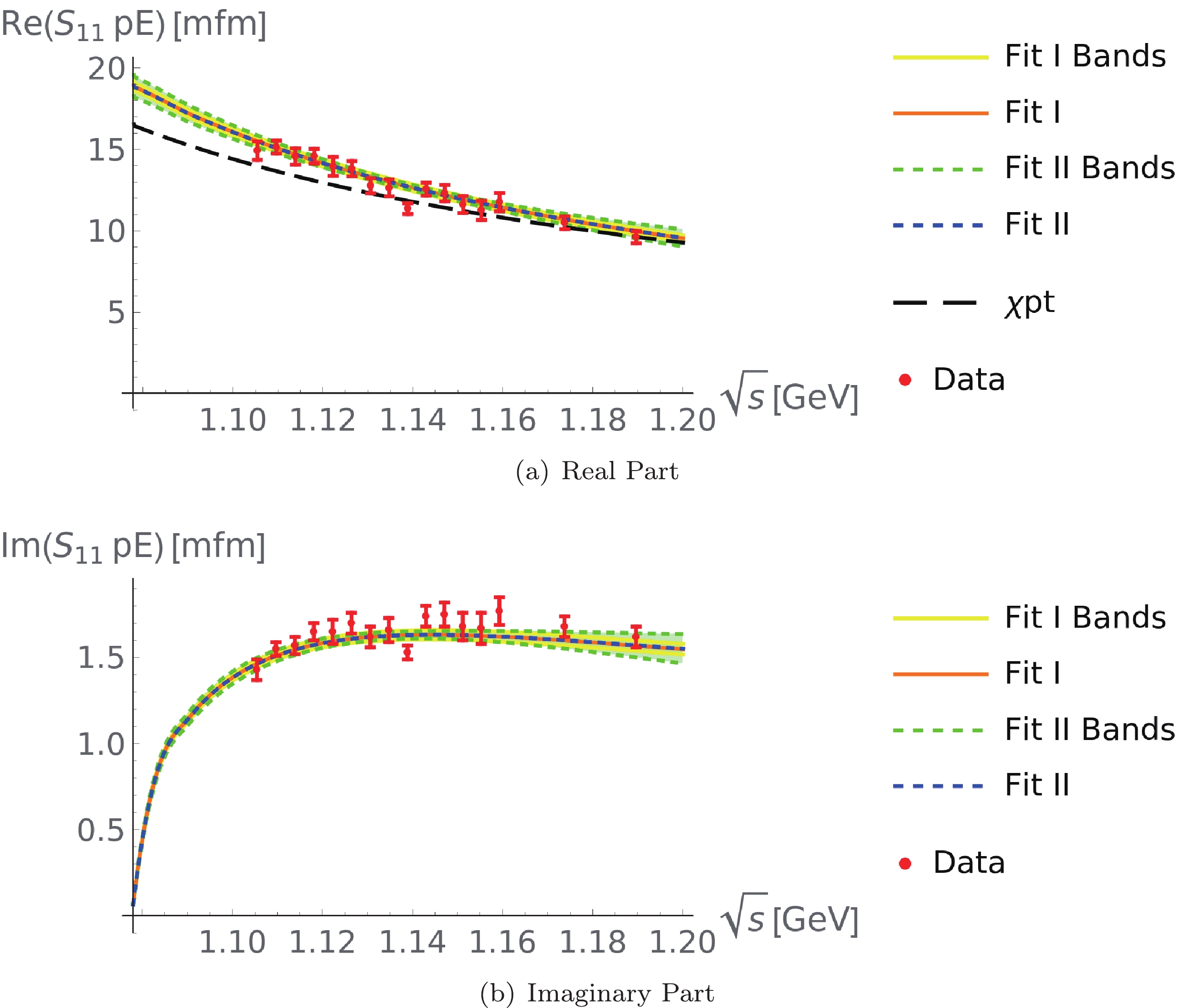
Figure 5. (color online)
$ p $ Target. (upper panel) Real part of the S$ _{11} $ electric multipole and (lower panel) imaginary part of the S$ _{11} $ electric multipole. The solid orange and dashed blue lines represent our dispersive descriptions based on Fit I and Fit II, respectively. The yellow solid line and green dashed line represent the error bands of Fit I and Fit II, respectively. For comparison, the chiral result of the real part of the multipole is also shown, corresponding to the black long dashed line.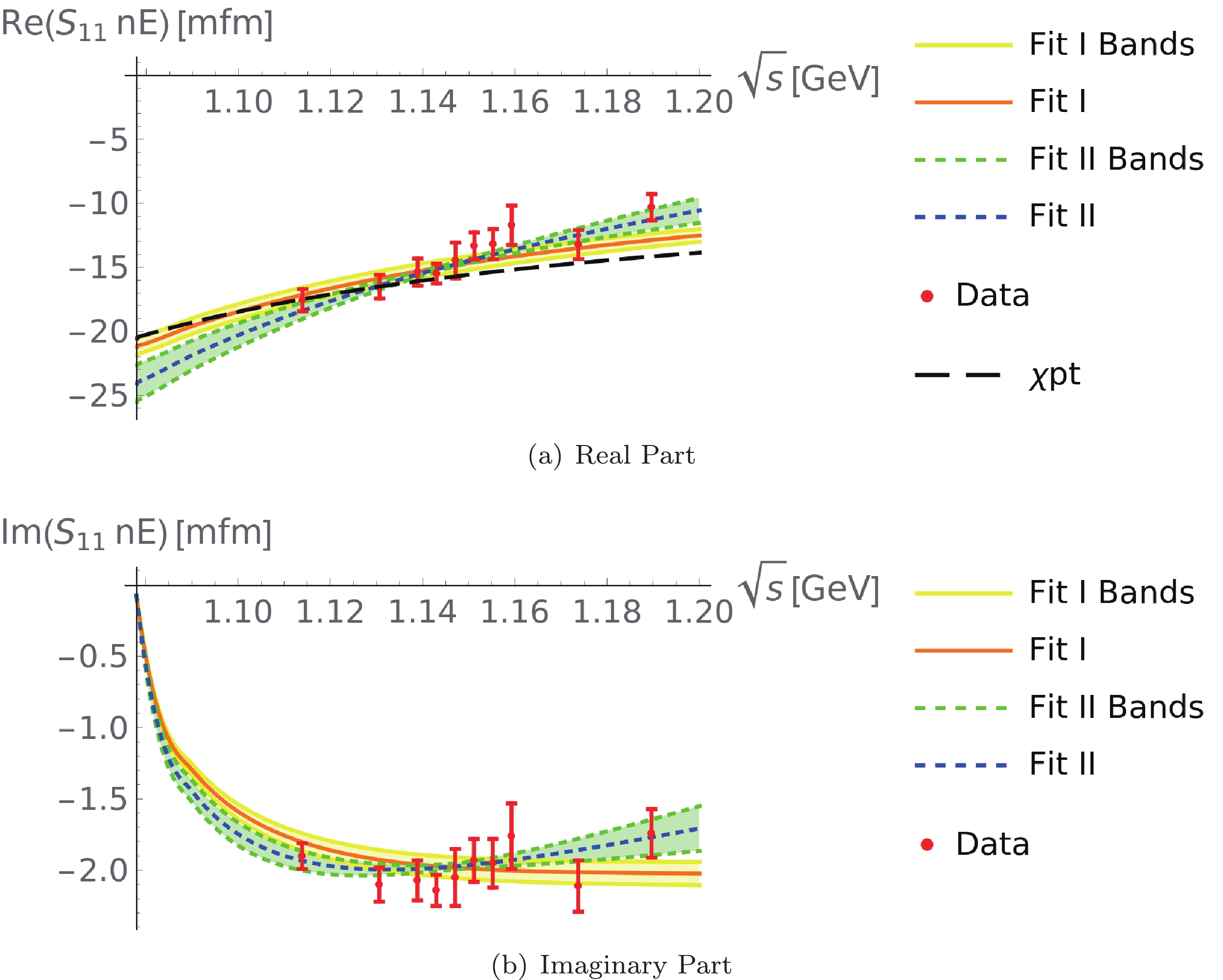
Figure 6. (color online)
$ n $ Target. Same definitions as in Fig. 5.For Fit I, our results are in good agreement with the experimental data in the sense that the averaged
$ \chi^2 $ values are close to one:$ \chi^2/{d.o.f} = 1.58 $ for the$ p $ target, and$ \chi^2/{d.o.f} = 1.22 $ for the$ n $ target. As can be seen from Table 2, the modulus of the central value of$ a $ is close to zero in the proton target case, while it is$ 1.43 $ in the neutron target case. This result is due to the fact that the electric multipoles calculated from BChPT in the proton case can describe the experimental data well, enforcing a nearly-zero contribution from the subtraction polynomial in the fitting procedure and further resulting in a nearly-zero value of$ a $ . However, in the neutron case, the discrepancy between BChPT results and experimental data is larger compared with the proton case, which leads to a larger central value (modulus) of$ a $ .Fit II is performed using a rank-2 subtraction polynomial with two parameters,
$ a $ and$ b $ . Compared with Fit I, the qualities of Fit II are improved, which is as expected because one more free parameter is involved in the fit procedure. However, the fitting parameters$ a $ and$ b $ of Fit II are highly correlated, with a correlation coefficient that is nearly$ -1 $ . Thus, Fit I is more advisable. -
In the previous subsection, all the parameters involved in the dispersive
$ S $ -wave photoproduction amplitude$ {\cal{M}}(s) $ were determined. Because$ N^\ast(890) $ , as a subthreshold resonance, is located on the second Riemann sheet (RS), analytic continuation is required to extract its couplings to the$ \gamma N $ and$ \pi N $ systems.The amplitude on the second RS can be deduced via
$ {\cal{M}}^{{\rm II}}(s) = \frac{{\cal{M}}(s)}{{\cal{S}}(s)}\ , $

(35) where
$ {\cal{M}}(s) $ is the partial-wave photoproduction amplitude given in Eq. (8), and$ {\cal{S}}(s) $ corresponds to the$ S $ matrix of$ \pi N $ scattering, with the same quantum numbers as$ {\cal{M}}(s) $ . If there exists a second RS pole located at$ z_R $ , the$ S $ matrix can be approximated by$ \begin{array}{l} {\cal{S}}(s)\approx {\cal{S}}'(z_{{\rm R}})\left(s-z_{{\rm R}}\right) \end{array} $

(36) in the vicinity of
$ z_{{\rm II}} $ . Thus,$ {\cal{M}}^{{\rm II}}(s) = \frac{{\cal{M}}(s)}{{\cal{S}}'(z_{{\rm R}})\left(s-z_{{\rm R}}\right)}\ . $

(37) Conversely, the couplings of this second RS pole to the
$ \gamma N $ and$ \pi N $ systems are defined as the residue via$ {\cal{M}}^{{\rm II}}(s\rightarrow z_{\rm R}) = \frac{g_{\gamma}g_{\pi}}{s-z_{\rm R}}\ , $

(38) with
$ g_\gamma $ and$ g_\pi $ denoting the$ \gamma N $ and$ \pi N $ couplings, respectively. Compared with Eq. (37), we obtain$ g_{\gamma}g_{\pi} = \frac{{\cal{M}}(z_{{\rm R}})}{{\cal{S}}'(z_{{\rm R}})}\ . $

(39) The
$ \pi N $ coupling can also be extracted from elastic$ \pi N $ scattering, i.e.,$ g_{\pi}^2 = \frac{{\cal{T}}(z_{{\rm R}})}{{\cal{S}}'(z_{{\rm R}})}\ , $

(40) where
$ {\cal{T}} $ is the corresponding partial-wave$ \pi N $ scattering amplitude.We now proceed with the numerical calculation of the couplings of
$ N^*(890) $ . According to Eqs. (39) and (B12), the pion photoproduction$ N^*(890) $ residue couplings, i.e.,$ g_{\gamma}g_{\pi} $ , can be extracted from the multipole amplitudes. In the meantime,$ g_{\pi}^2 $ can be computed using Eq. (40), which was already done in Ref. [19]. Results of the couplings are listed in Table 3. The results based on Fit II are also shown to verify the stability of the obtained values. We employed two solutions for the pole position of the$ N^*(890) $ , i.e.,$ \sqrt{s} = 0.882-0.190{\rm i} $ , corresponding to the cutoff$ s_c = -1 $ GeV, and$ \sqrt{s} = 0.960-0.192{\rm i} $ , corresponding to$ s_c = -9 $ GeV; see Ref. [19] for a detailed explanation.$ g_{\gamma}g_{\pi} $ 

$ g_{\pi}^2 $ 

Fit I Fit II target pole position moduli phase moduli phase moduli phase p $ 0.882-0.190{\rm i} $ 

$ \left(1.212\pm0.014\right) $ 

$ -79.2\pm1.3 $ 

$ 1.203\pm 0.302 $ 

$ -78.9\pm 11.4 $ 

$ 19.7\pm 0.3 $ 

$ 32.6\pm1.0 $ 

$ 0.960-0.192{\rm i} $ 

$ \left(1.467\pm0.016\right) $ 

$ -71.3\pm0.9 $ 

$ 1.459\pm 0.279 $ 

$ -71.2\pm3.5 $ 

$ 21.4\pm 0.2 $ 

$ 33.6\pm 0.8 $ 

n $0.882-0.190{\rm i}$ 

$ \left(0.6416\pm0.0265\right) $ 

$ 111\pm7 $ 

$ 2.025\pm 0.731 $ 

$ 81.4\pm 6.9 $ 

$ 0.960-0.192{\rm i} $ 

$ \left(1.111\pm0.050\right) $ 

$ 103\pm3 $ 

$ 2.342\pm 0.605 $ 

$ 98.0\pm 1.5 $ 

Table 3. Results of
$ g_{\gamma}g_{\pi} $ and$ g_{\pi}^2 $ . Pole position, moduli, and phase are in units of$ \rm{GeV} $ ,$ 10^{-2}\; \rm{GeV^2} $ , and degrees, respectively.$ g_{\pi}^2 $ values are the same for the p target and n target because of the isospin symmetry.In the extraction of
$ g_{\gamma}g_{\pi} $ and$ g_{\pi}^2 $ of$ N^*(890) $ ,$ z_{\rm R} $ is treated as the$ N^*(890) $ pole position in the$ s $ plane,$ {\cal{M}}(z_{\rm R}) $ can be obtained from the dispersion relation in Eq. (8) once$ {\cal{P}} $ is determined,$ {\cal{T}}(z_{\rm R}) $ can be obtained through$ {\cal{S}}(z_{\rm R}) = 1+2{\rm i}\rho_{\pi N}{\cal{T}} = 0 $ , and$ \frac{1}{S'(z_{\rm R})} $ is simply the residue of$ {\cal{S}}^{\rm II} $ from Ref. [19]. However, to compare the results of$ N^*(1535) $ , which are extracted directly from multipole amplitudes parameterized in the$ \sqrt{s} $ plane in Ref. [39], the conventions should be consistent. In the S$ _{11} $ channel, the following equation can be used to translate these residues from different conventions into residues directly extracted from multipole amplitudes in the$ s $ plane.$\begin{aligned}[b] E^{I = \frac{1}{2}\ \rm II}_{0+}(s\rightarrow z_{\rm R}) =& -\sqrt{\frac{2}{3s}}\frac{g_{\gamma}g_{\pi}}{s-z_{\rm R}} \\=&-\sqrt{\frac{2}{3s}}\frac{g_{\gamma}g_{\pi}}{2\sqrt{z_{\rm R}}(\sqrt{s}-\sqrt{z_{\rm R}})}\ ,\end{aligned} $

(41) where
$ {\rm R} $ stands for$ N^*(890) $ or$ N^*(1535) $ . In S$ _{11}pE $ , the modulus of the residue is$ 2.41\;\rm{mfm\cdot GeV^2} $ with phase$ 120^\circ $ ; meanwhile, the magnitude of$ N^*(1535) $ residue coupling from Ref. [39] is approximately$ 0.736 \;\rm{mfm\cdot GeV^2} $ , and the phase is$ -27^\circ $ . The magnitude of the$ N^*(890) $ residue is thus larger than that of the$ N^*(1535) $ residue. The$ |g_{\pi}^2| $ of$ N^*(890) $ is$ 0.2\;\rm{GeV}^2 $ , and that of$ N^*(1535) $ , which is obtained using the value in Ref. [45], is$ 0.08\;\rm{GeV}^2 $ . The$ g_{\pi}^2 $ of these two resonances may account for part of the reason why$ N^*(890) $ photoproduction residue is large, and using the above results,$ g_{\gamma} $ for these two resonances can be obtained. The$ |g_{\gamma}| $ of$ N^*(890) $ is$ 0.032\;\rm GeV $ , while that of$ N^*(1535) $ is$ 0.024\;\rm GeV $ , so it is clear that the magnitudes are almost the same. Note that the results of the n target are quite unstable. The fact that data points are few, having large error bars, may account for the main reason.We can also calculate the decay amplitude
$ {\cal{A}}^{\frac{1}{2}} $ at the$ N^\ast(890) $ pole position, which is related to the coupling$ g_{\gamma} $ , using the equation given in Ref. [39]:$ {\cal{A}}^{\frac{1}{2}} = g_{\gamma}\sqrt{\frac{\pi}{q_r^2m_N}\rho_{\gamma N}}\ , $

(42) where
$ q_r $ is the modulus of the photon momentum calculated at the resonance pole position.Furthermore, we can obtain the partial widths of the
$ N^*(890)\to\gamma N $ channel at the pole using the following equation, which is from Ref. [46] and converted to our convention:$ \Gamma_{\gamma N} = \left\lvert\rho_{\gamma N}\frac{g_{\gamma}^2}{\sqrt{z_{\rm R}}}\right\rvert \ , $

(43) where
$ z_{\rm R} $ is treated as the$ N^*(890) $ pole position. The values of the decay amplitudes$ {\cal{A}}^{\frac{1}{2}} $ and the partial decay width at the pole$ \Gamma_{\gamma N} $ are presented in Table 4.target pole position $ {\cal{A}}^{\frac{1}{2}} $ 

$ \Gamma_{\gamma N} $ 

Fit I Fit II Fit I Fit II moduli phase moduli phase p $ 0.882-0.190{\rm i} $ 

$ 0.165\pm 0.004 $ 

$ -129\pm2 $ 

$ 0.165\pm0.043 $ 

$ -129\pm12 $ 

$ 0.369\pm0.014 $ 

$ 0.363\pm0.210 $ 

$ 0.960-0.192{\rm i} $ 

$ 0.191\pm0.004 $ 

$ -43.4\pm1.4 $ 

$ 0.191\pm0.038 $ 

$ -43.3\pm3.9 $ 

$ 0.396\pm0.013 $ 

$ 0.391\pm0.168 $ 

n $ 0.882-0.190{\rm i} $ 

$ 0.0879\pm0.0043 $ 

$ 61.7\pm8.2 $ 

$ 0.277\pm0.102 $ 

$ 31.4\pm7.4 $ 

$ 0.103\pm0.011 $ 

$ 1.03\pm0.89 $ 

$ 0.960-0.192{\rm i} $ 

$ 0.145\pm0.008 $ 

$ 130\pm4 $ 

$ 0.305\pm0.096 $ 

$ 125\pm 3 $ 

$ 0.227\pm0.023 $ 

$ 1.01\pm0.73 $ 

Table 4. Values of the decay amplitude (
$ {\cal{A}}^{\frac{1}{2}} $ ) and decay width ($ \Gamma_{\gamma N} $ ) calculated at the$ N^\ast(890) $ pole position. Phase,$ {\cal{A}}^{\frac{1}{2}} $ , and$ \Gamma_{\gamma N} $ are in degrees,$ {\rm GeV^{-\frac{1}{2}}} $ , and$ \rm MeV $ , respectively.The
$ |{\cal{A}}^{\frac{1}{2}}| $ of$ N^*(890) $ is larger than that of$ N^*(1535) $ , which is$ 0.074 \;\rm GeV^{-\frac{1}{2}} $ , with the phase being$ -17^\circ $ in S$ _{11}pE $ from Ref. [39], but the decay widths at the pole are almost the same, regardless of the instability of the n target results. -
In this paper, we have performed a careful dispersive analysis of the process of single pion photon production off the nucleon, in the S
$ _{11} $ wave of the final pion-nucleon system. In such a dispersive representation, the right-hand cut contribution can be related to an Omnés solution, which takes the elastic$ \pi N $ phase shifts as inputs, and hence is known up to a polynomial. Conversely, we estimate the left-hand cut contribution by making use of the$ {\cal{O}}(q^2) $ tree amplitudes taken from chiral perturbation theory. A detailed discussion of how to establish a proper analytic structure of the partial-wave pion photon production amplitude is also presented for easy reference in the future. To pin down the free parameters in the dispersive amplitude, we perform fits to experimental data of multipole amplitudes in the channels, indicated by S$ _{11}pE $ and S$ _{11}nE $ , for energies ranging from the$ \pi N $ threshold to$ 1.440\; \rm GeV^2 $ .The experimental data can be well described by the dispersive amplitude with only one free subtraction parameter. We then continue the dispersive amplitude to the second Riemann sheet to be able to extract the couplings of
$ N^\ast $ to the$ \gamma N $ and$ \pi N $ systems, which are denoted by$ g_\gamma $ and$ g_\pi $ , respectively. Based on the obtained value of$ g_\gamma g_\pi $ , the modulus of the corresponding residue of the multipole amplitude (S$ {_{11}pE} $ ) at the$ N^\ast(890) $ pole position is$ 2.41\;\rm{mfm\cdot GeV^2} $ , which is much larger than the modulus of the residue of$ N^\ast(1535) $ , i.e.,$ 0.736\; \rm{mfm\cdot GeV^2} $ [39]. This result means that the strength of the interaction of$ N^\ast(890) $ with the$ \pi N $ system is stronger than that for$ N^\ast(1535) $ . It is physically reasonable and within expectation because$ N^\ast(890) $ is thought to be composed of the$ \pi N $ system, and it is well-known that$ N^\ast(1535) $ has a tiny coupling with$ \pi N $ , as we all know. The results provides further evidence of existence of$ N^\ast(890) $ . As byproducts, the decay amplitude and the decay width at the$ N^\ast(890) $ pole position$ {\cal{A}}_h $ and the$ \Gamma_{\gamma N} $ are obtained for future reference. -
The authors are grateful to Y. F. Wang for valuable discussions.
-
The functions
$ {({\cal{G}}_{H_s}^{J})}_i $ defined in Eq. (31) are shown for the S$ _{11} $ wave in the following:$\tag{A1} \begin{aligned}[b] {( {\cal{G}}_{+++}^{J = \frac{1}{2}})}_1 = {\rm i}k_1 \sqrt{s} \left(k_l k_r \left(m_N^2\!-\!s\right)-m_N^2\left(m_{\pi }^2\!+\!2 s\right)+m_N^4\!+\!s \left(-m_{\pi }^2\!+\!s\!+\!2t\right)\right) \times {\left(\left(m_N^2\!-\!s\right) \left(\left(m_N\!-\!m_{\pi}\right){}^2\!-\!s\right) \left(\left(m_N+m_{\pi }\right){}^2\!-\!s\right)\right)}^{-1}\ , \end{aligned} $

$ \tag{A2} {( {\cal{G}}_{++-}^{J = \frac{1}{2}})}_1 \!=\! -{\rm i}k_2 \sqrt{s} \left(k_l k_r \left(s\!-\!m_N^2\right)-m_N^2\left(m_{\pi }^2\!+\!2 s\right)+m_N^4\!+\!s \left(-m_{\pi }^2\!+\!s\!+\!2t\right)\right)\times {\left(\left(m_N^2\!-\!s\right) \left(\left(m_N-m_{\pi}\right){}^2\!-\!s\right) \left(\left(m_N+m_{\pi }\right){}^2\!-\!s\right)\right)}^{-1}\ , $

$\tag{A3} {( {\cal{G}}_{+++}^{J = \frac{1}{2}})}_2 = {\rm i} s \left(k_1 \sqrt{s}-k_2 m_N\right) \left(m_N^2\left(m_{\pi }^4-t \left(m_{\pi }^2+2 s\right)\right)+t m_N^4+s t\left(-m_{\pi }^2+s+t\right)\right)\times {\left(\left(m_N^2-s\right){}^2\left(\left(m_N-m_{\pi }\right){}^2-s\right) \left(\left(m_N+m_{\pi}\right){}^2-s\right)\right)}^{-1}\ , $

$\tag{A4} {( {\cal{G}}_{++-}^{J = \frac{1}{2}})}_2 = {\rm i} s \left(k_1 m_N-k_2 \sqrt{s}\right) \left(m_N^2\left(m_{\pi }^4-t \left(m_{\pi }^2+2 s\right)\right)+t m_N^4+s t\left(-m_{\pi }^2+s+t\right)\right)\times {\left(\left(m_N^2-s\right){}^2\left(\left(m_N-m_{\pi }\right){}^2-s\right) \left(\left(m_N+m_{\pi}\right){}^2-s\right)\right)}^{-1}\ , $

$\tag{A5} \begin{aligned}[b] {( {\cal{G}}_{+++}^{J = \frac{1}{2}})}_3 =& -k_2 \left(m_N^2 \left(k_l k_r-m_{\pi }^2-2 s\right)+s\left(-k_l k_r-m_{\pi }^2+s+2 t\right)+m_N^4\right)\times \Biggl[ k_l k_r\left(\frac{2 k_1 \sqrt{s} m_N \left(m_{\pi }^2-t\right)}{k_2}-m_N^2 \left(m_{\pi }^2+2 s\right)+m_N^4+s\left(m_{\pi }^2+s\right)\right) \\&- \left(m_N^2-s\right)\left(\left(m_N-m_{\pi }\right){}^2-s\right) \left(\left(m_N+m_{\pi}\right){}^2-s\right)\Biggl ]\times {\left(4 \left(m_N^2-s\right){}^2\left(s-\left(m_N-m_{\pi }\right){}^2\right){}^{3/2}\left(s-\left(m_N+m_{\pi }\right){}^2\right){}^{3/2}\right)}^{-1}\ , \end{aligned} $

$\tag{A6} \begin{aligned}[b] {( {\cal{G}}_{++-}^{J = \frac{1}{2}})}_3 =& k_1 \left(-m_N^2 \left(k_l k_r+m_{\pi }^2+2s\right)+s \left(k_l k_r-m_{\pi }^2+s+2 t\right)+m_N^4\right)\times \Biggl[k_l k_r \left(\frac{2 \sqrt{s} m_N \left(m_{\pi }^2-t\right)k_2}{k_1}-m_N^2 \left(m_{\pi }^2+2 s\right)+m_N^4+s \left(m_{\pi}^2+s\right)\right) \\&+ \left(m_N^2-s\right) \left(\left(m_N-m_{\pi}\right){}^2-s\right) \left(\left(m_N+m_{\pi}\right){}^2-s\right)\Biggl]\times {\left(4 \left(m_N^2-s\right){}^2\left(s-\left(m_N-m_{\pi }\right){}^2\right){}^{3/2}\left(s-\left(m_N+m_{\pi }\right){}^2\right){}^{3/2}\right)}^{-1}\ , \end{aligned} $

$\tag{A7} \begin{aligned}[b] {( {\cal{G}}_{+++}^{J = \frac{1}{2}})}_4 =& \left(k_l k_r \left(m_N^2-s\right)-m_N^2 \left(m_{\pi }^2+2s\right)+m_N^4+s \left(-m_{\pi }^2+s+2 t\right)\right) \Biggl[k_2 k_l k_r\left(-2 \sqrt{s} m_N \left(-m_{\pi }^2+2 s+t\right)-m_N^2 \left(m_{\pi}^2-2 s\right)+m_N^4\right.\\&\left.+s \left(m_{\pi }^2-3 s\right)\right) + 4 k_1 \sqrt{s}k_l k_r m_N^3-k_2 \left(m_N^2-s\right) \left(\left(m_N-m_{\pi}\right){}^2-s\right) \left(\left(m_N+m_{\pi}\right){}^2-s\right)\Biggl]\\&\times {\left(4 \left(m_N^2-s\right){}^2\left(s-\left(m_N-m_{\pi }\right){}^2\right){}^{3/2}\left(s-\left(m_N+m_{\pi }\right){}^2\right){}^{3/2}\right)}^{-1}\ , \end{aligned} $

$\tag{A8} \begin{aligned}[b] {( {\cal{G}}_{++-}^{J = \frac{1}{2}})}_4 =& \left(k_l k_r \left(m_N^2-s\right)+m_N^2 \left(m_{\pi }^2+2s\right)-m_N^4+s \left(m_{\pi }^2-s-2 t\right)\right)\times \Biggl[2 k_2 \sqrt{s}k_l k_r m_N \left(2 m_N^2+m_{\pi }^2-2 s-t\right)+k_1 \left(m_N^2-s\right)\\&\times \left(k_l k_r \left(m_N^2-m_{\pi }^2+3 s\right)-2 m_N^2 \left(m_{\pi}^2+s\right)+m_N^4+\left(m_{\pi }^2-s\right){}^2\right)\Biggl]\times {\left(4\left(m_N^2-s\right){}^2 \left(s-\left(m_N-m_{\pi}\right){}^2\right){}^{3/2} \left(s-\left(m_N+m_{\pi}\right){}^2\right){}^{3/2}\right)}^{-1} \end{aligned} $

with
$\tag{A9} \begin{aligned}[b] k_l =& \sqrt{s-s_{\rm L}}\ , \\ k_r =& \sqrt{s-s_{\rm R}}\ , \\ k_1 =& \sqrt{s+m_N^2-m_{\pi}^2-\sqrt{s-s_{\rm R}}\sqrt{s-s_{\rm L}}}\ ,\\ k_2 =& \sqrt{s+m_N^2-m_{\pi}^2+\sqrt{s-s_{\rm R}}\sqrt{s-s_{\rm L}}}\ . \end{aligned} $

The amplitudes
$ A_{i}(s,t) $ up to$ {\cal{O}}(q^2) $ contain the following terms:●
$ t $ channel pion exchange:$ \frac{1}{t-m_{\pi}^2} $ ;●
$ u $ channel nucleon exchange:$ \frac{1}{u-m_N^2} = \frac{1}{m_N^2+m_{\pi}^2-s-t} $ ;● Kinematic decomposition:
$ \frac{1}{P\cdot q} = \frac{4}{t-2 m_N^2-m_{\pi }^2+2s} $ .They lead to logarithm terms:
$\tag{A10} \begin{aligned}[b] {\cal{D}}_1 =& \ln \left(-\sqrt{s-s_{\rm L}} \sqrt{s-s_{\rm R}}+m_N^2-m_{\pi }^2+s\right) \\ & -\ln \left(\sqrt{s-s_{\rm L}} \sqrt{s-s_{\rm R}}+m_N^2-m_{\pi }^2+s\right)\ , \end{aligned} $

$\tag{A11} \begin{aligned}[b] {\cal{D}}_2 =& \ln \left(-\sqrt{s-s_{\rm L}} \sqrt{s-s_{\rm R}}-m_N^2+m_{\pi }^2+s\right) \\ & -\ln \left(\sqrt{s-s_{\rm L}} \sqrt{s-s_{\rm R}}-m_N^2+m_{\pi }^2+s\right)\ , \end{aligned} $

$ \tag{A12}\begin{aligned}[b] {\cal{D}}_3 =& \ln \left(\sqrt{s-s_{\rm L}} \sqrt{s-s_{\rm R}}+m_N^2-m_{\pi }^2+3 s\right) \\ & -\ln \left(-\sqrt{s-s_{\rm L}} \sqrt{s-s_{\rm R}}+m_N^2-m_{\pi }^2+3 s\right)\ . \end{aligned} $

-
Traditional pion photoproduction partial wave analysis is in CGLN amplitudes (
$ {\cal{F}} $ ) with$ \tag{B1} \frac{{\rm d}\sigma}{{\rm d}\Omega} = \frac{q'}{q}\left\lvert\langle\chi_f\lvert{\cal{F}}\rvert\chi_i\rangle\right\rvert^2\ , $

where
$ \chi_{i(f)} $ is the Pauli spinor and$\tag{B2} \begin{aligned}[b] {\cal{F}} =& {\rm i}\vec{\sigma}\cdot\vec{\epsilon}{\cal{F}}_1+\left(\vec{\sigma}\cdot\vec{q'}\right)\vec{\sigma}\cdot\left(\vec{q}\times\vec{\epsilon}\right){\cal{F}}_2 \\& +{\rm i}\left(\vec{\sigma}\cdot q\right)\left(\vec{q'}\cdot\vec{\epsilon}\right){\cal{F}}_3+{\rm i}\left(\vec{q'}\cdot\vec{\sigma}\right)\left(\vec{q'}\cdot\vec{\epsilon}\right){\cal{F}}_4\ , \end{aligned} $

where there are four independent amplitudes. The connection of our scattering amplitudes to
$ {\cal{F}} $ can be obtained as follows:$\tag{B3} {\cal{M}}_{fi} = 8\pi\sqrt{s}{\cal{F}}_{fi}\ , $

where the subscripts
$ f,\ i $ mean that the initial and final states are substituted into Eq. (B2), which we will omit in the following discussion.Furthermore, the partial wave amplitude
$ {\cal{F}}^J $ is defined in Ref. [3]:$ \tag{B4} {\cal{F}}_{\pm;\lambda_r}^J = \frac{1}{4\pi}\int_{-1}^{1}\int_{0}^{2\pi} F_{\pm;\lambda_r}D^J(\theta,\phi){\rm d}\Omega\ , $

where
$ \pm $ denote the final nucleon helicity, and$ \lambda_r = \frac{1}{2}\ \text{or}\ \frac{3}{2} $ , which is the modulus of the initial helicity. Also, definite parity amplitudes can be obtained:$\tag{B5} \begin{aligned}[b] A_{n+} =& -\frac{1}{\sqrt{2}}\left({\cal{F}}_{+,\frac{1}{2}}^{J}+{\cal{F}}^{J}_{-,\frac{1}{2}}\right)\ , \\ A_{\left(n+1\right)-} =& \frac{1}{\sqrt{2}}\left({\cal{F}}_{+,\frac{1}{2}}^{J}-{\cal{F}}^{J}_{-,\frac{1}{2}}\right)\ , \\ B_{n+} =& \sqrt{\frac{2}{n\left(n+2\right)}}\left({\cal{F}}_{+,\frac{3}{2}}^{J}+{\cal{F}}^{J}_{-,\frac{3}{2}}\right)\ ,\\ B_{\left(n+1\right)-} =& -\sqrt{\frac{2}{n\left(n+2\right)}}\left({\cal{F}}_{+,\frac{3}{2}}^{J}-{\cal{F}}^{J}_{-,\frac{3}{2}}\right)\ , \end{aligned} $

where
$ A_{n\pm},B_{n\pm} $ are amplitudes with$ J = n\pm\frac{1}{2} $ and$ P = -{\left(-1\right)}^n $ .According to Ref. [3], the following relation between CGLN partial wave amplitudes (
$ A_{n\pm} $ and$ B_{n\pm} $ ) and multipole amplitudes ($ E_{n\pm} $ and$ M_{n\pm} $ ) can be obtained:$ \tag{B6} E_{0+} = A_{0+}\ , $

$\tag{B7} M_{1-} = A_{1-}\ . $

and for
$ l\geqslant 1 $ $\tag{B8} E_{l}+ = {(l+1)}^{-1}\left(A_{l+}+\frac{1}{2}lB_{l+}\right)\ , $

$\tag{B9} M_{l}+ = {(l+1)}^{-1}\left(A_{l+}-\frac{1}{2}\left(l+2\right)B_{l+}\right)\ , $

$\tag{B10} E_{(l+1)-} = -{(l+1)}^{-1}\left(A_{(l+1)-}-\frac{1}{2}\left(l+2\right)B_{(l+1)-}\right)\ , $

$\tag{B11} M_{(l+1)-} = {(l+1)}^{-1}\left(A_{(l+1)-}+\frac{1}{2}lB_{(l+1)-}\right)\ . $

Furthermore, consider the fact that
$ E^{I = \frac{1}{2}}_{0+} $ is not normalized in isospin space, according to Refs. [47] and [48]; therefore, we have an additional$ \sqrt{3} $ in the normalization factor, and the relation in the$ S_{11} $ channel can be obtained as follows:$ \tag{B12} E_{0+}^{I = \frac{1}{2}} = -\sqrt{\frac{2}{3s}}{\cal{M}}\left(S_{11}\right)\ , $

where
$ E_{0+}^{I = \frac{1}{2}} $ is the conventional multipole amplitude, and$ 0 $ and$ + $ refer to the S wave and minus parity, respectively.
Dispersive analysis of low energy γN→πN process and studies on the N*(890) resonance
- Received Date: 2020-06-02
- Available Online: 2021-01-15
Abstract: We present a dispersive representation of the






 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF
























 DownLoad:
DownLoad: