-
Long ago, Fred Hoyle [1] proposed the possibility of a 0+ resonance near the three
$ \alpha $ threshold in 12C: the Hoyle state (HS). Today, clustering is still a topic of significant interest in nuclear structure studies for C and more complex nuclei [2-25]. This is true for nuclear dynamics as well, for instance in fragmentation reactions [26-33], together with the possibility of observing Bose Einstein condensates (BECs) and Efimov states (ESs) [22, 34]. In Refs. [35, 36], we have extended the study of 12C to ‘in medium’ decays by studying three$ \alpha $ correlations for 70Zn+70Zn, 64Zn+64Zn, and 64Ni+64Ni heavy ion collisions at 35 MeV/u; the corresponding experiment was performed at the Cyclotron Institute, Texas A&M University [32]. Following Refs. [37, 38], we searched events with all of the$ \alpha $ particles in a mutual resonance through the ground state of 8Be. If this mechanism captures an excited level of 12C, it should be located at 7.46 MeV, just below the HS. Because of the lower excitation energy with respect to the HS, its decay probability is strongly hindered [38]. The situation might change ‘in medium’ if in heavy ion collisions an$ \alpha $ -BEC is strongly resonating through the ground state of 8Be. This implies that all of the relative energies of three$ \alpha $ (two by two) are equal to 92 keV; this state has been dubbed the Thomas state (TS) in Refs. [39, 40]. Following Ref. [39], we identified the HS as the ES [34, 41, 42] because of its 100% decay into 8Be+$ \alpha $ ; i.e, with the lowest relative energy of two$ \alpha $ equal to 92 keV. The mechanism is that an interaction between two$ \alpha $ particles is mediated by a third$ \alpha $ particle. This boson mediation produces an effective field that binds the three particle system [40].This mechanism may be extended to four or more bosons [43] and can provide novel insights into many body interactions. In particular, if 16O can be described as four
$ \alpha $ clusters, we can study the relative energy distributions of all six possible two$ \alpha $ combinations.On one hand, if 16O decays into four
$ \alpha $ at once, then its Q-value will be -14.44 MeV, and the six relative energy combinations will equal 92 keV (the 8Be ground state). Therefore, we expect an excited level at E* = 14.72 MeV [43]. The Coulomb field and the finite$ \alpha $ -$ \alpha $ interaction range may preclude its occurrence [34, 41, 43]. This mechanism has been observed in atoms [44] for three particles, and a possible extension to N$ > $ 3 boson systems is currently investigated [43]. On the other hand, similar to the situation for 12C [35, 36], we expect an excited level of 16O, which decays sequentially to 12C(HS)+$ \alpha $ with 12C(HS) decaying into 8Be+$ \alpha $ [45-48]. In this case the available excitation energy is not divided ‘democratically’ (equally) among all the$ \alpha $ particles. Only the lowest relative energy of two$ \alpha $ particles is equal to 92 keV (the last 8Be decay). Recently [18, 21], this level has been observed experimentally around the 15.2 MeV excitation energy of 16O, but was not confirmed in Ref. [22], probably owing to insufficient statistical evidence in the energy region of interest. We notice that in the region near the 14.72 MeV excitation energy, many energy levels [49] have been observed close to the neutron decay threshold and a few MeV above the proton decay threshold. Thus, the decay into four$ \alpha $ might have been missed in those experiments owing to the low tunneling probability.In the present work, we carefully investigated the decay of 16O into four
$ \alpha $ particles, using available fragmentation data. The remainder of this paper is organized as follows: Sec. II briefly describes the experimental setupand summarizes the analysis method of selecting and reconstructing events. In Sec. III, we analyze the important ingredients from relative-kinetic-energy distributions of two$ \alpha $ particle data and the energy correlation function of 16O from four$ \alpha $ particle data. We conclude and summarize our work in Sec. IV. -
The beams of 70Zn, 64Zn, and 64Ni at 35 MeV/u were produced by the K500 Superconducting Cyclotron at the Texas A&M University Cyclotron Institute, and collided with 70Zn, 64Zn, and 64Ni self-supporting targets, respectively. Fragments were measured on an event-by-event basis, using a 4
$ \pi $ array Neutron Ion Multidetector for Reaction Oriented Dynamics with the Indiana Silicon Sphere (NIMROD-ISiS), which consisted of 14 concentric rings, covering from 3.6° to 167° in the laboratory frame [50, 51]. In the forward rings covering from 3.6° to 45°, two modules were set. The supertelescope modules had two Si detectors (150 and 500 μm) placed in front of a CsI(Tl) detector (3-10 cm). The telescope modules in the forward and backward rings had one Si detector (either 150, 300, or 500 μm) followed by a CsI(Tl) detector. Light charged particles with Z = 1-3 were identified using the pulse shape discrimination method by the CsI(Tl) detectors. Intermediate mass fragments (IMFs) were identified by the telescopes and supertelescopes, using the ‘$ \Delta $ E-E’ method. In the forward rings, isotopic resolution of up to Z = 12 and elemental identification of up to Z = 20 were achieved. In the backward rings, only Z = 1-2 particles were identified, owing to the detector energy thresholds. Further experimental details can be found in Refs. [25, 29, 30, 32, 50, 51].We emphasize that only the events with
$ \alpha $ multiplicity equal to four were analyzed, and the results for the three nuclear collision systems were combined, to improve the statistical evidence. The same approach was used for the 12C analysis [35, 36]. The momenta of$ \alpha $ particles can be measured very well. A major problem arises when the relative kinetic energy of the two$ \alpha $ particle system becomes as low as tens of keV; then, the particles are detected by two nearby detectors (or by the same one). Owing to the limited size (finite granularity) of the detectors, angle and relative momentum errors arise. We note that all detectors suffer from this problem, and the resulting error or minimal measurable relative kinetic energy is on the order of 40 keV [9, 10, 25]; the better the granularity, the smaller the error. Our method has an obvious advantage, because our beam energy is close to the Fermi energy; that is, the kinetic energy of each ion is high, above a few MeV/u [32, 36]. This is ideal for our detector. To detect the low energy excited levels of 8Be, 12C, and 16O, the relative kinetic energy should be very low.Let us start by recalling the expression for the excitation energy E* of 16O decaying into four
$ \alpha $ particles with the Q-value, Q = −14.44 MeV. This expression is given by Eq. (1):$ {E^*} = \frac{1}{2}\sum\limits_{i = 1,j > i}^4 {{E_{ij}}} - Q, $

(1) where
${{E}}_{ij} $ is the relative energy of the two$ \alpha $ particle system, and we have classified (undistinguishable)$ \alpha $ particles according to their relative energies, such that${{E}}_{ij}^{1} \leqslant{{E}}_{ij}^{2} \leqslant \dots \leqslant {{E}}_{ij}^{6}$ .Using Eq. (1) we can easily estimate excited levels for 16O, assuming that we have not one but two HSs in 16O. In the rest frame of 8Be (8Beg.s.), we assumethat the energy of each of the two
$ \alpha $ particles is that of the HS of 12C. Thus, the excitation energy of 16O in this configuration is given by E*(16O) = 2*0.235+0.092+14.44 = 15.0 (MeV), i.e., very close to the suggested level [18, 21, 22], where 0.235 MeV is the relative energy of the two$ \alpha $ particle system from the decay of 12C in the HS, 0.092 MeV is the energy of 8Beg.s., and 14.44 MeV is the Q-value [35, 36]. We stress that calculating the tunneling probability for such a configuration at this stage can be tricky, since the intermediate state involves 12C that is not in the ground state. Thus, reactions for the excited levels of 12C may occur with higher probability, as discussed in [52]; this will be addressed elsewhere. We note that the occurrence of the excited level of 16O at 15.0 MeV, as discussed above, involves multiple resonances in the 8Be+$ \alpha $ +$ \alpha $ system similar to the Efimov mechanism [34, 40-44]; thus, a careful investigation is needed.The proposed analysis relies heavily on the detector performance. The finite granularity of the detector (like all detectors) demands making some choices, which becomes crucial when searching for fine details. Because of the finite granularity, the first important choice is to assign a position to a fragment in a single detector. Commonly, two possible avenues are followed [10, 32, 53]. One is to assign the fragment position at the center of a single detector (CD). Another approach is to assign a random position on the surface of a single detector (RD). While the first approach is sufficient for determining resonances within the reach of the detector granularity, the second approach spreads the resonance but is sensitive to resonances located at even lower excitation energies. Thus, the two approaches are somewhat complementary, and we will analyze our data using both. The RD approach is advantageous compared with the CD one, because it allows to randomly choose the positions of real events N
$ > >1 $ times (RDN). Thus, we can uniformly cover the detector surface and, by normalizing, we obtain the probability of finding a fragment at a certain angle and energy. This procedure (not to be confused with the mixing method discussed below) smoothens the fluctuations owing to statistics or resonances; as a result, if two resonances have sufficiently similar energies, they cannot be distinguished. Of course, for wide relative angles between the two fragments and sufficient amounts of data, the RD(N) and CD methods yield similar results.Another detector feature to consider is the phenomenon of double hits (DHs). Because of the finite granularity, it is possible that two fragments will hit the same detector during the same event. The signals induced by DHs of
$ \alpha $ -particles are quite unique, and such DH events can be distinguished clearly from other fragments, such as 6,7Li [53]. However, only the total energy of the two$ \alpha $ particles can be determined, without informing about the energies of individual particles. Ref. [53] adopted the ‘democratic’ assumption that the total energy is equally divided between the two fragments. This, together with the CD method, automatically yieldsa ‘resonance’ for relative energies${{E}}_{ij} $ (DH) = 0 MeV. The RD(N) method, on the other hand, may yields a non-zero relative energy, since the positions of the two particles in the single detector are randomly chosen. As we have discussed in Ref. [35] for the 12C case (for which the RD method was adopted), the lowest relative energy of two$ \alpha $ particles peaked at 92 keV after correcting for the detector acceptance. This result suggests that the DH energy choice${{E}}_{ij} $ (DH) can be modified to 92 keV; clearly, this assumption, especially for the CD case, will improve the 8Be resonance decay. Below, we will show that it is amply justified.Notice that real events exhibit strong quantum correlations, since
$ \alpha $ particles are not distinguishable bosons; thus, at low excitation energies or temperatures, they might be in a BEC. Therefore, the next step in the data analysis is to generate mixing events for each assumption discussed above. This is achieved by choosing four different$ \alpha $ -particles from four different events. This procedure can be repeated many times (more than the number of real events), yielding a smooth benchmark of the available phase space. When events are mixed, quantum correlations are lost, and the distribution can be described as a classical one or a Maxwell-Boltzmann distribution. In the absence of resonances, we expect the correlation function to be given by the ratio of the Bose-Einstein distribution divided by the Maxwell-Boltzmanndistribution opportunely corrected by Coulomb interactions[54]. Strong resonances, especially close to the threshold, may dominate the correlation function; this can be inferred from data, as we show below. As for real events, we normalize the total number of mixing events to 1. A four-body correlation function can be defined as$ 1+R_4 = \frac{Y_{\rm R}}{Y_{\rm M}}, $

(2) where
${{Y}}_{\rm R} $ is the yield of real events and${{Y}}_{\rm M} $ is the yield of mixing events. Similarly, three-body (1+${{R}}_{3} $ ) and two-body (1+${{R}}_{2} $ ) correlation functions can be obtained. The ratio can be reported as a function of the 16O excitation energy defined in Eq. (1) or other relevant physical quantities. In Ref. [35], we have defined an alternative way of deriving correlation functions using the transverse energy distribution ($ E_{\rm T} $ ) instead of the mixing events technique. This is based on the same assumption that for equilibrated systems, the transverse and total energy distributions are the same, apart from the trivial 3/2 scaling factor [35].A major problem in our analysis is the detector acceptance. Most of our results provide circumstantial evidence of low energy resonances, and using the methods discussed here with more performing detectors would be crucial for shedding some light on the discussed mechanisms. Of course, a perfect 4
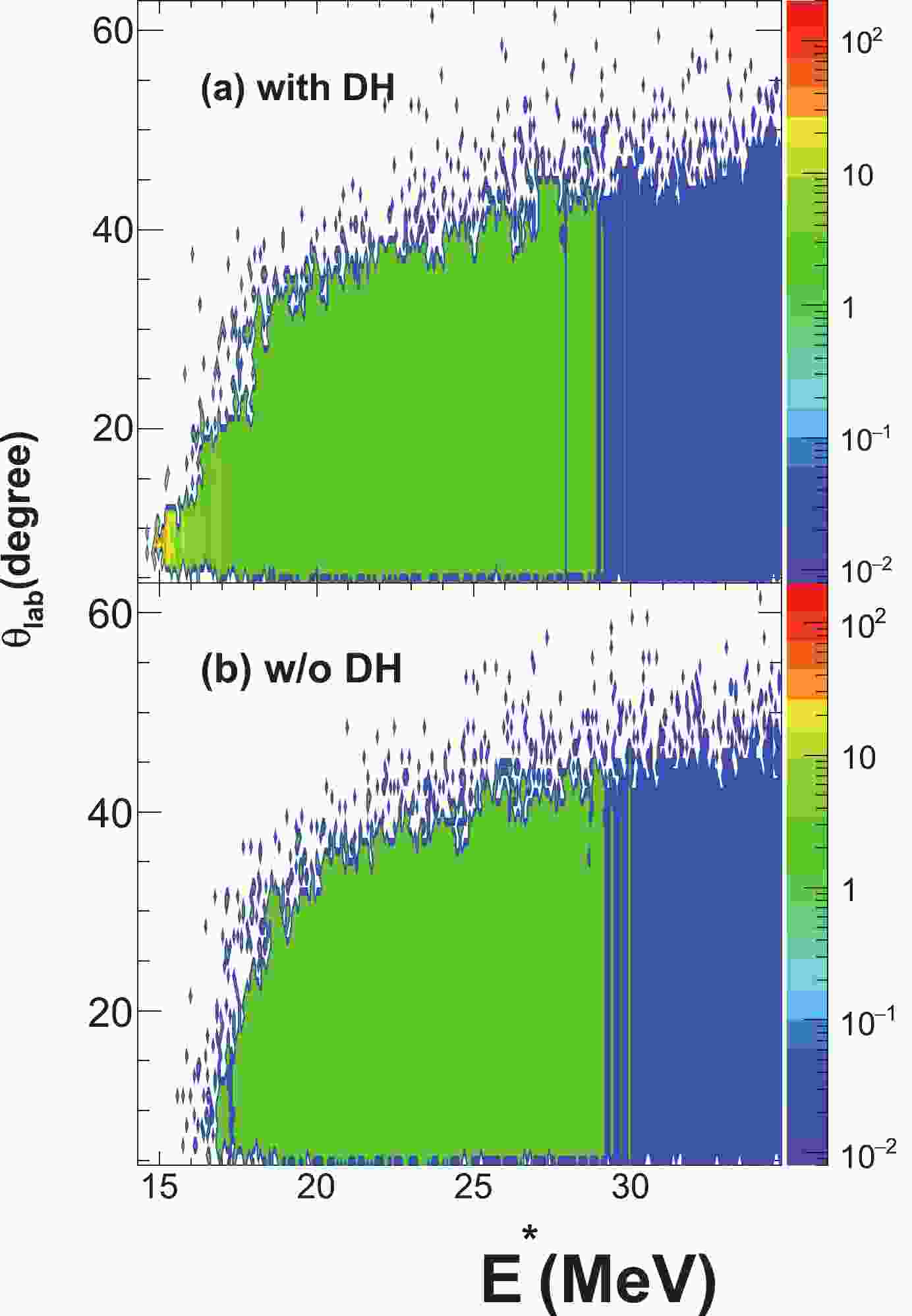
$ \pi $ detector is quite impossible to realize; thus, it is very important to optimize it according to the studied phenomena. For$ \alpha $ particles generated in heavy ion collisions, it is important to select those events that yield the largest number of correlated particles. In our experiment, this can be easily visualized by deriving the average angle for$ \alpha $ particles (i.e., average over the four$ \alpha $ particle angles for each event), as a function of the$E^* $ of 16O. In Fig. 1 we plot such a distribution, with the color encoding the value of 1+${{R}}_4 $ . Evidently, the correlation function is above 1 for energies below 30 MeV, where many 16O resonances are observed. These events are associated with narrow angles, suggesting peripheral collisions with a low deposited excitation energy. In particular, excitation energies near 15 MeV correspond to angles below 15 degrees. Thus, for improving the call sensitivity, a larger granularity is required, especially for those forward angles. -
Following Ref. [35], we plot the distributions of relative energies of the two body system, for the RDN case, in Fig. 2, with similar results to those of the 12C case. In the top panels, the bumps obtained for real events (solid black circles) are owing to the decays of 8Be, 12C, and 16O into
$ \alpha $ particles, and owing to completely non-correlated processes; for instance, a heavy fragment can emit$ \alpha $ particles as well [32, 36]. To distinguish correlated events from non-correlated events, in Fig. 2, we show the distributions for mixing events using red open circles. The counts of both real and mixing events are normalized to one. The two distributions look similar on the logarithmic scale, but significantly differ for low relative kinetic energies. For low relative kinetic energies, the distribution of real events in Fig. 2(a) shows a downward trend, while those in (b)-(f) show upward trends. As mentioned earlier, when the relative kinetic energy becomes very low, it becomes difficult to allocate the detection angle, owing to the granularity of the detector. Of course, this is less important for the situation in Figs. 2(b)-(f), since the relative kinetic energy of the event obtained in the first panel is the lowest.To correct this feature, we use an exponential function to fit the highest point in Fig. 2(a). This allows us to estimate the instrument error as$ \Delta $ E = 1/22 MeV = 0.045 MeV, which is slightly higher than that reported in Refs. [9-17] but sufficiently low to let us derive the results discussed below. Clearly, Figs. 2(b)-(f) show that the experimental error is less important, and the slope change is approximately 0.1 MeV (8Beg.s.$ _{\rm g.s.} $ ). To determine the resonances, we can use the same slope (or experimental error) as before for the exponential fitting, and reproduce the experimental point at 0.045 MeV. By subtracting the fits from the real events, we obtain the results marked by open squares in Fig. 2, which can be regarded as the real events corrected by the detector acceptance. Evidently, all six cases show a bump at approximately 0.08 MeV (very close to 0.092 MeV), corresponding to the decay of 8Beg.s.$ _{\rm g.s.} $ . According to our ranking of these two$ \alpha $ particle system relative kinetic energies, we infer that if the maximal relative kinetic energy is 0.092 MeV, then the other five kinetic energies must also be 0.092 MeV (because they are smaller). Therefore, we have four$ \alpha $ particles in a mutual resonance, which is a mechanism similar to the ESs of exchanging a boson between the other two [34, 37, 41]. If this cannot be related to the characteristics of the strong resonant boson gas [6], then it may be an unexplored 16O state at${{E}} ^* $ = 14.72 MeV (as given by Eq. (1)). The calculations in Ref. [38] suggest that when 12C is formed in a vacuum, its observation probability is eight orders of magnitude smaller than that of the HS. In a medium, owing to the presence of other fragments, the mechanism of mutual resonances may be enhanced. After subtracting the exponential fit, the ratio of the real (green squares) to the mixing events (red open circles) gives the correlation functions 1+${{R}} _2 $ , shown in the bottom panels of Fig. 2. The ratio reveals peaks around 0.08 MeV, for all cases.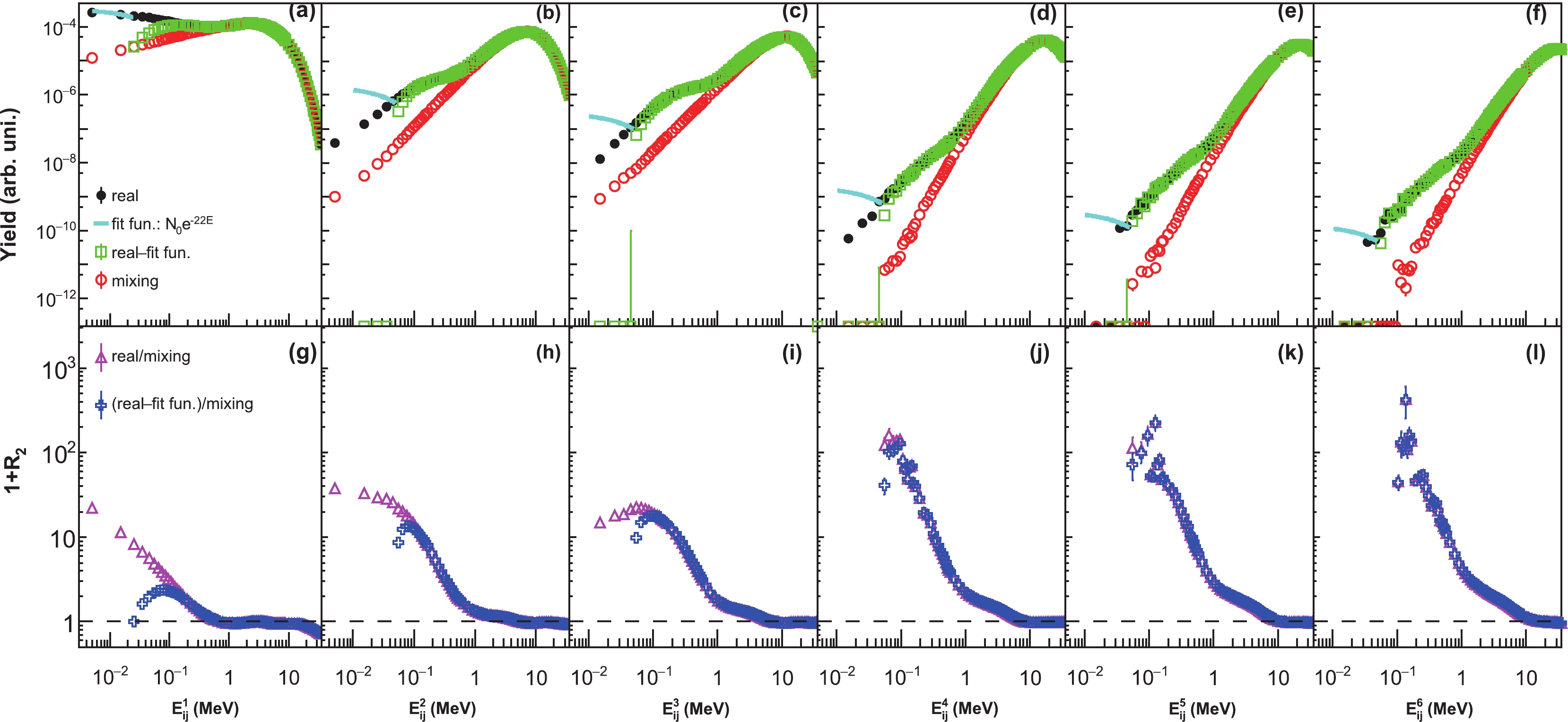
Figure 2. (color online) Selected events for
$^{70(64)}$ Zn(64Ni) +$^{70(64)}$ Zn(64Ni) at E/A = 35 MeV/u, with$\alpha$ multiplicity equal to four, for our RDN method. Relative kinetic energy distributions vs. the relative kinetic energy of two$\alpha$ particles, shown in the order of${{E}}_{ij}^{1}\leqslant {{E}}_{ij}^{2}\leqslant\dots\leqslant{{E}}_{ij}^{6}$ for panels (a)-(f). The solid black circles are for real events, the red open circles are for mixing events, and the green open squares are for the difference between the real events and the exponential function (solid curve), which accounts for the experimental error. The ratios of the real (pink open triangles) data and the real data minus the fitting function (blue crosses) divided by the mixing events are shown vs. the relative kinetic energy of two$\alpha$ particles, in the order of${{E}}_{ij}^{1}\leqslant{{E}}_{ij}^{2}\leqslant \dots \leqslant{{E}}_{ij}^{6}$ for panels (g)-(l).To assess the DH effect on the relative kinetic energy, we added the
${{E}} _{ij} $ (DH) = 92 keV (middle panels) and no DH (bottom panel) cases to the RDN case, and show the results in Fig. 3. Some important points are worth stressing by inspecting Fig. 3. First, for higher relative energies, the results with and without the exponential subtraction are the same (top panels). Second, all the relative energies exhibit a peak around 92 keV, thus confirming the occurrence of strong resonances in the BEC (top and middle panels).${{E}} _{ij} $ (DH) = 92 keV (middle panels) does not need any exponential correction, indicating that the RDN method plus the choice${{E}} _{ij} $ (DH) = 92 keV is sufficient for inferring energy levels. The original${{E}} _{ij} $ increases the correlation function at low energies and needs a correction for consistency with the${{E}} _{ij} $ (DH) = 92 keV case. Finally, in the bottom panel, we show the results without DH. This shows that the RDN method can be used for determining the 92 keV resonance but it needs DH for revealing the 8Be resonance for all relative energy combinations.
Figure 3. (color online) The 1+R2 correlation function vs the
$\alpha$ -$\alpha$ relative energy, for all possible combinations. The events are shown in the order of${{E}}_{ij}^{1} \leqslant{{E}}_{ij}^{2} \leqslant \dots \leqslant{{E}}_{ij}^{6}$ . The results for the RDN method with${{E}}_{ij}$ original (top),${{E}}_{ij}$ (DH) = 92 keV (middle), and no DH (bottom) are plotted vs. the relative energy. In the top panels, the exponential correction to the detector acceptance case is denoted by the open circles [35].For completeness, we repeated the analysis for the CD case; the results are shown in Fig. 4. There are some differences in the choice of the relative energy for DHs, but we notice that this choice is complementary to the RDN case, because the peak near 92 keV is evident already for the smallest
${{E}} _{ij}^1 $ without any correction for the experimental acceptance and no DH.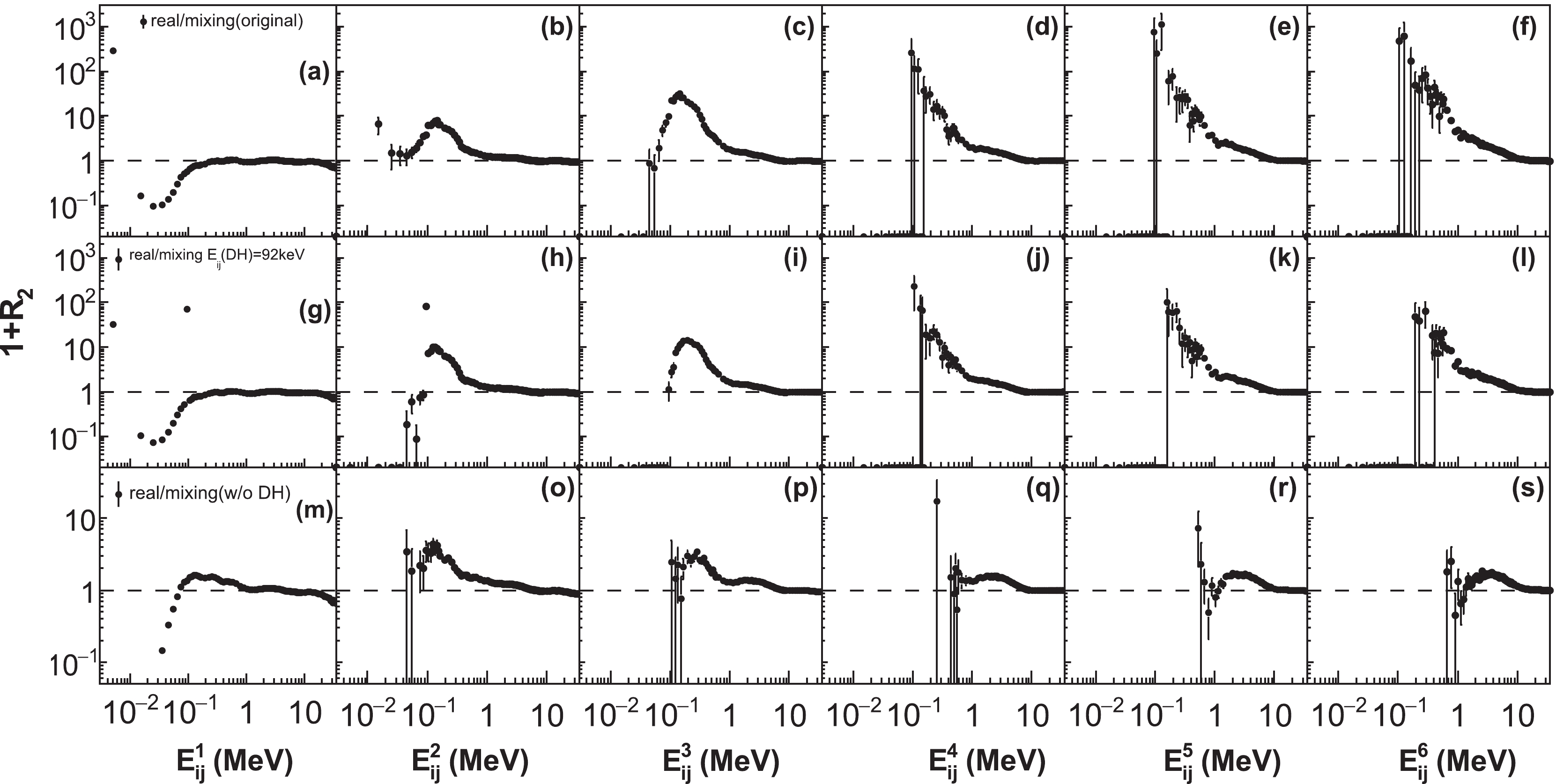
Figure 4. Same as for Fig. 3, but for the CD case. The
${{E}}_{ij}$ original (top),${{E}}_{ij}$ (DH) = 92 keV (middle), and no DH (bottom) cases exhibit multiple resonances at 92 keV. For larger relative energies, the results for the 92 keV case shift to higher energies, owing to insufficient statistics and finite detector granularity.In Fig. 5, we plot the excitation energy distributions (a-c) and the energy correlation function (d-f) of 16O, for four
$ \alpha $ particles. In panels (a,d),${{E}} _{ij} $ (DH) = 92 keV was adopted, while the original${{E}} _{ij} $ (i.e.${{E}} _{ij} $ = 0 MeV) is considered in panels (b,e). The results obtained without DH are shown in panels (c,f). Evidently, in panels (d-f), the CD case (black full circles) yields a positive correlation approximately at 15 MeV. A peak at 15.2 MeV is clearly seen when the${{E}} _{ij} $ (DH) = 92 keV assumption is adopted. The RDN events (red open circles) show a smoothening of the CD case (see also the insets). One interesting feature is that two clear peaks appear at 14.85 MeV and 15.2 MeV in panel (d), while the two peaks are smoothened in panel (e). The CD case is smoothened into one large peak in the RDN case. With the original choice for the DH, we observe a decreasing trend of the correlation function. Panel (f) (no DH) shows the positive correlation function above 15 MeV but no data points are found for lower energies; thus, it suggests that the DH relevance for the decay of 8Be is crucial for determining the exact position of the resonance (s). Another important ingredient in the data analysis displayed in Fig. 5 is the bin-width, which was set to 60 keV. Larger bin-widths smoothen fluctuations, and may increase the resonance width.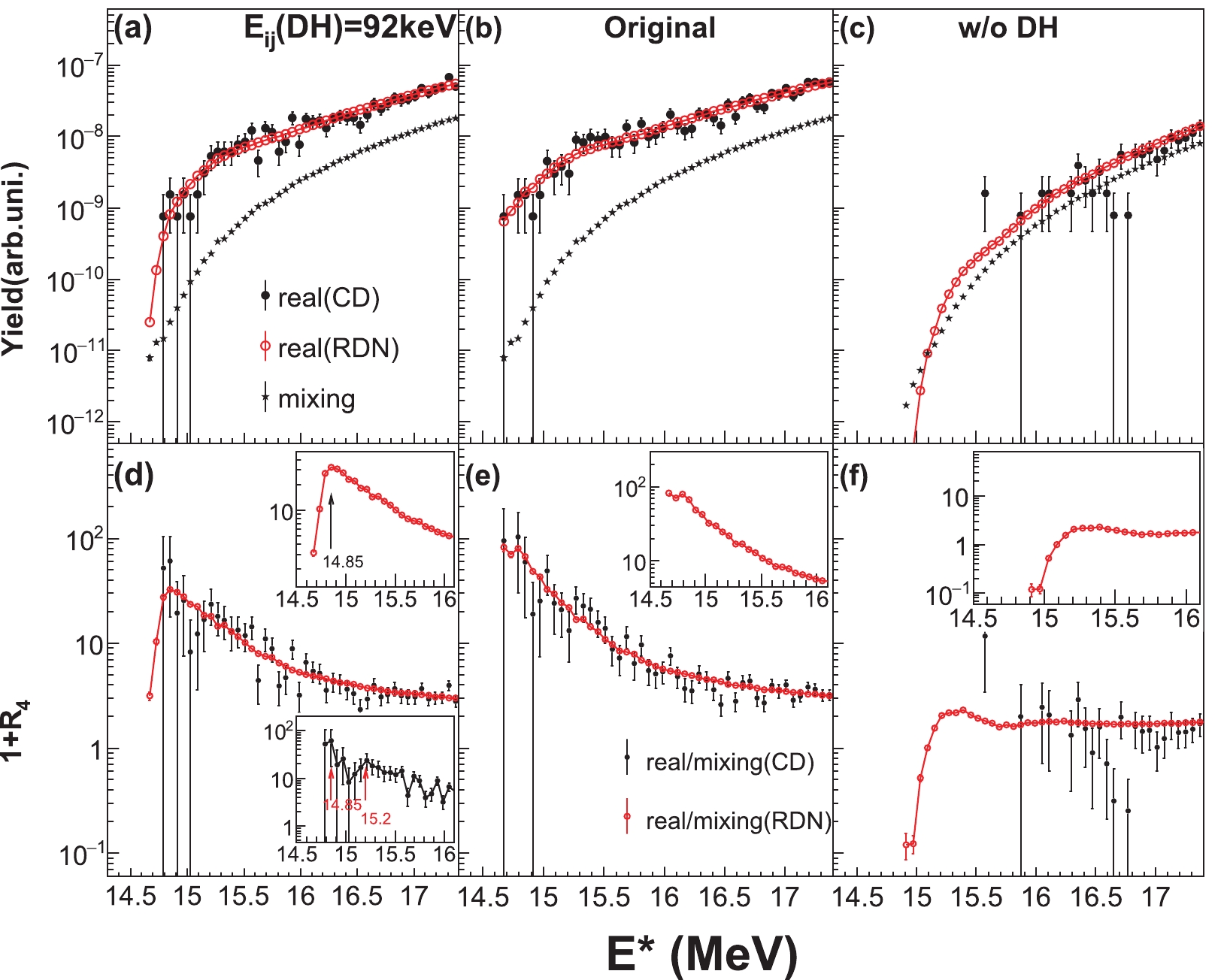
Figure 5. (color online) The energy correlation function of 16O for four
$\alpha$ particles: (a) relative energy for DH is equal to 92 keV and (b) original. No DHs in panel (c). In all cases, the bin-width was set to 60 keV. In the insets we show the results for the RDN cases only.We repeated the previous analysis (Fig. 5) for different bin-widths; the results are shown in Fig. 6, with (a), (b), (c), and (d) showing the results for the bin-widths of 60, 80, 120, and 200 keV, respectively, and similarly for the middle and bottom panels and for the CD case only. Note that 15.2 MeV is clearly visible in the two top panels, with some hints in the bottom panel where DH was not included. Some data points are also present near the 14.85 MeV excitation energy, but the error bars are too large. In the inset of Fig. 6(d), we have indicated the positions and widths of some observed excited levels attributed to the decays into 8Be+8Be (black full lines) and
$ \alpha $ +12C*(HS) (red dashed lines) [45-48]. We notice a large bump below 16 MeV, which might be dominated by the suggested resonances plus the detector acceptance. For higher excitation energies, the resonances are embedded into the BEC; thus, they are not clearly distinguishable [26, 30, 31]. Of course, repeating the experiment with better detector granularity might shed more light on these medium levels. In such a scenario, the RDN method proposed in this work might be crucial.
Figure 6. (color online) Excitation energy distributions for the CD case: (top)
${{E}}_{ij}$ (DH) = 92 keV, (middle)${{E}}_{ij}$ original, and (bottom) no DHs. Panels (a), (b), (c), and (d) correspond to the bin-widths of 60, 80, 120, and 200 keV, and the middle and bottom panels are similar. In the inset of (d), the positions and widths of known resonances are indicated as well (see main text).For completeness, we have repeated the analysis for the CD case using the transverse energy method, to derive the correlation function as in Ref. [35]. In Fig. 7, we plot the correlation functions for different bin widths; these results should be compared with those in Fig. 6. This method is in agreement with the mixing method and actually shows a sharper resonance at lower excitation energies.
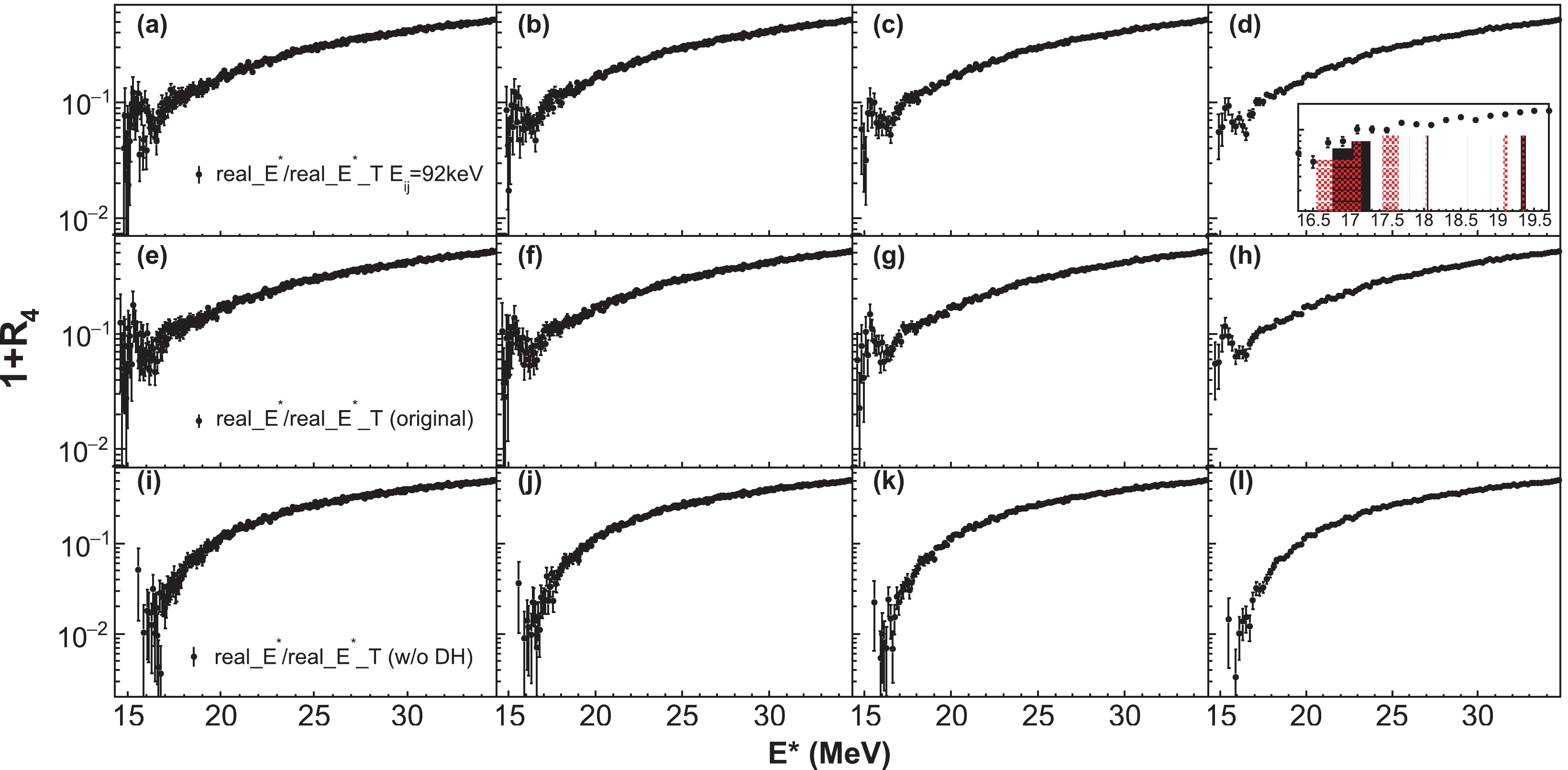
Figure 7. (color online) Transverse excitation energy distributions for the CD case: (top)
${{E}}_{ij}$ (DH) = 92 keV, (middle)${{E}}_{ij}$ original, and (bottom) no DHs. Panels (a), (b), (c), and (d) correspond to the bin-widths of 60, 80, 120, and 200 keV, and the middle and bottom panels are similar. In the inset of (d), the positions and widths of known resonances are indicated as well (see main text). -
In conclusion, in this paper, we have shown that strong resonances among
$ \alpha $ -particles occur in fragmentation reactions; these resonances could be a signature of a BEC. Furthermore, strong correlations at relative energies${{E}} _{ij}^{1} \leqslant{{E}}_{ij}^{2} \leqslant \dots \leqslant{{E}}_{ij}^{6} $ confirm the boson exchange mechanism [43] and the possibility of an excited level of 16O at 14.72 MeV. Experimental search for this resonance in reactions with no medium effects (for instance p+$ ^{15}{\rm{N}}\rightarrow $ 8Be+8Be$ \rightarrow $ 4$ \alpha $ ,$ {{J}}^{\pi} $ = 0+) would be extremely interesting, but we anticipate a very low decay cross section, owing to the Coulomb barrier and the competition with other open channels. Nevertheless, the presence of multiple resonances might modify the probabilities substantially [52]. We have also confirmed the resonance in 16O at 15.2 MeV [21, 22].
Four α correlations in nuclear fragmentation: a game of resonances
- Received Date: 2020-05-01
- Available Online: 2021-02-15
Abstract: Heavy ion collisions near the Fermi energy produce a ‘freezout’ region where fragments appear and later decay, emitting mainly neutrons, protons, alpha particles, and gamma rays. These decay products carry information about the decaying nuclei. Fragmentation events may result in high yields of boson particles, especially alpha particles, and may carry important information about the nuclear Bose Einstein condensate (BEC). We study ‘in medium’ four α correlations and link them to the ‘fission’ of 16O in two 8Be in the ground state or 12C*(Hoyle state)+α. Using novel techniques for the correlation functions, we confirm the resonance of 16O at 15.2 MeV excitation energy, and the possibility of a lower resonance, close to 14.72 MeV. The latter resonance is the result of all α particles having 92 keV relative kinetic energies.





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF














 DownLoad:
DownLoad: