On possible implications of the exponential distribution of constituent quarks within proton at high energies

Investigating the partonic structure of the proton has generated significant interest over the past decades. Deep inelastic scattering (DIS) is a clean process to study the proton's internal structure through interaction with virtual photons. A specific type of DIS process, called the diffractive (or vector meson production) process, is particularly suitable for probing the spatial structure of the proton because there is no color exchange between the virtual photon and the proton. This process requires the exchange of two gluons during the interaction, leading to the diffractive cross-section being proportional to the squared scattering amplitude, which means the vector meson production process is highly sensitive to the QCD dynamics compared to inclusive DIS. Furthermore, there are no color strings between the virtual photon and the proton, resulting in a rapidity gap (a region in rapidity with no particles produced), which is an effective signature used experimentally to identify the diffractive events from the total DIS events. More importantly, the diffractive cross-section is associated with the Fourier transforms between the transverse momentum transfer ($ {\boldsymbol{\Delta}} $) and impact parameter ($ {\boldsymbol{b}} $), where $ {\boldsymbol{b}} $ points to the center of the dipole from the center of the proton. The dependence of the diffractive cross-section on $ {\boldsymbol{b}} $ indicates that the diffractive process is sensitive to the proton's transverse profile. This demonstrates that the diffractive DIS process can serve as a powerful tool to probe the geometric structure of the proton. Therefore, the particular process we use to explore the proton's partonic structure is the diffractive DIS.

Several approaches are used to calculate the electron-proton diffractive cross-sections in the literature [1−6]. One novel method, inspired by the requirement of fluctuating geometric shape of the proton in describing high multiplicity proton-proton and proton-nucleus collisions, is the hot spot model (HSM) which was established on top of the impact parameter dependent saturation (IPsat) model with the proton profile function modified by the constituent quark picture [7, 8]. In the hot spot model, it is assumed that the constituent quarks distribute randomly within the proton, and the positions of the constituent quarks follow a Gaussian distribution. The constituent quarks emit gluons individually at high energies. The emitted gluons form a "cloud" around the constituent quarks, respectively. This gluon "cloud" is also known as a hot spot. Therefore, in the HSM, the proton profile function is a summation of the three constituent quarks' density functions instead of a simple Gaussian function, and the proton profile function varies from event to event. The HSM provides a rather successful description of the vector meson production data at HERA in the relatively small momentum transfer region, especially for incoherent $ J/\Psi $ production. The diffractive cross-section without a fluctuating geometric shape underestimates the measured incoherent cross-section of $ J/\Psi $ production by several orders of magnitude [8]. Unfortunately, for coherent $ J/\Psi $ production, there is some tension between the HSM and currently available HERA data in the relatively large $ |t| $ region ($ 1\sim1.5\; \mathrm{GeV}^2 $) [8]. The HSM dramatically underestimates the measurements of the coherent cross-section of the $ J/\Psi $ production in this regime.

In this paper, we investigate why the HSM underestimates the coherent cross-section of $ J/\Psi $ production in the relatively large $ |t| $ region, and we find that the position distribution function of the constituent quarks within the proton significantly influences the coherent cross-section when $ |t| $ is larger than $ 1.0\; \mathrm{GeV}^2 $. Therefore, we modify the Gaussian position distribution of the constituent quarks used in the HSM with several types of distribution functions to improve the capability of the HSM. To demonstrate the improvement of our modified HSM, we calculate the coherent and incoherent cross-sections as a function of $ |t| $, and the coherent cross-sections as a function of center of mass energy (W) with both the original and modified HSMs for $ J/\Psi $ production, and compare the results with HERA data, respectively. It shows that both the original and modified HSMs provide similar quality descriptions of the incoherent HERA data, indicating that the incoherent process cannot be used to probe the position distribution of the constituent quarks within the proton. For the coherent $ J/\Psi $ production in the small $ |t| $ region ($ |t|<1\; \mathrm{GeV}^2 $), we find no significant difference between the descriptions of the original and modified HSMs. However, our calculations show that only the modified HSM with an exponential position distribution can provide a reasonable description of the coherent $ J/\Psi $ production data at the relatively large $ |t| $ region, while the original HSM dramatically underestimates the coherent $ J/\Psi $ production in this $ |t| $ regime. This outcome suggests a possible implication of an exponential distribution of constituent quarks within the proton at high energy.

The diffractive vector meson production process in electron-proton deep inelastic scattering is usually described by the Good-Walker picture, which classifies the processes into two types: coherent and incoherent, in terms of whether the scattered target proton breaks up or not [9]. The coherent cross-section, corresponding to the process where the target proton remains intact after the scattering, can be obtained by averaging over the target proton wave function at the amplitude level [1, 2]

where $ \langle\cdots\rangle $ represents the average over configurations of the proton wavefunction. The $ \gamma^* $, p, and V in Eq. (1) denote the virtual photon, proton, and vector meson. The x, $ Q^2 $, and $ {\boldsymbol{\Delta}} $ in Eq. (1) are the longitudinal momentum fraction of the proton transferred to the vector meson, photon virtuality, and momentum transfer (with $ {\boldsymbol{\Delta}}^2=-t $), respectively. The $ \mathcal{A}^{\gamma^*p\rightarrow Vp} $ is the scattering amplitude, which will be discussed in detail later.

In the Good-Walker picture, the incoherent cross section, corresponding to the process where the target proton is broken after the scattering, can be written as the variance [3, 10],

To clearly see the features of the coherent and incoherent cross sections, we compare Eq. (1) with Eq. (2). We can see that the coherent cross section performs the average on the level of the scattering amplitude; it is proportional to the average configuration of the proton, which provides the overall parton distribution information of the proton. In contrast, the incoherent cross section reflects the variance of the proton profile, being sensitive to the structural fluctuations of the proton.

Let us now introduce the scattering amplitude, $ \mathcal{A}^{\gamma^*p\rightarrow Vp} $. In this paper, we calculate the $ \gamma^*p $ scattering amplitude based on the Color Glass Condensate (CGC) framework and color dipole picture, where at high energy, the virtual photon splits into a quark-antiquark ($ q\bar{q} $) dipole; then the $ q\bar{q} $ dipole interacts with the proton target, followed by the recombination of the $ q\bar{q} $ dipole into the vector meson, see Fig. 1. The scattering amplitude for the vector meson production can be written as [2, 11]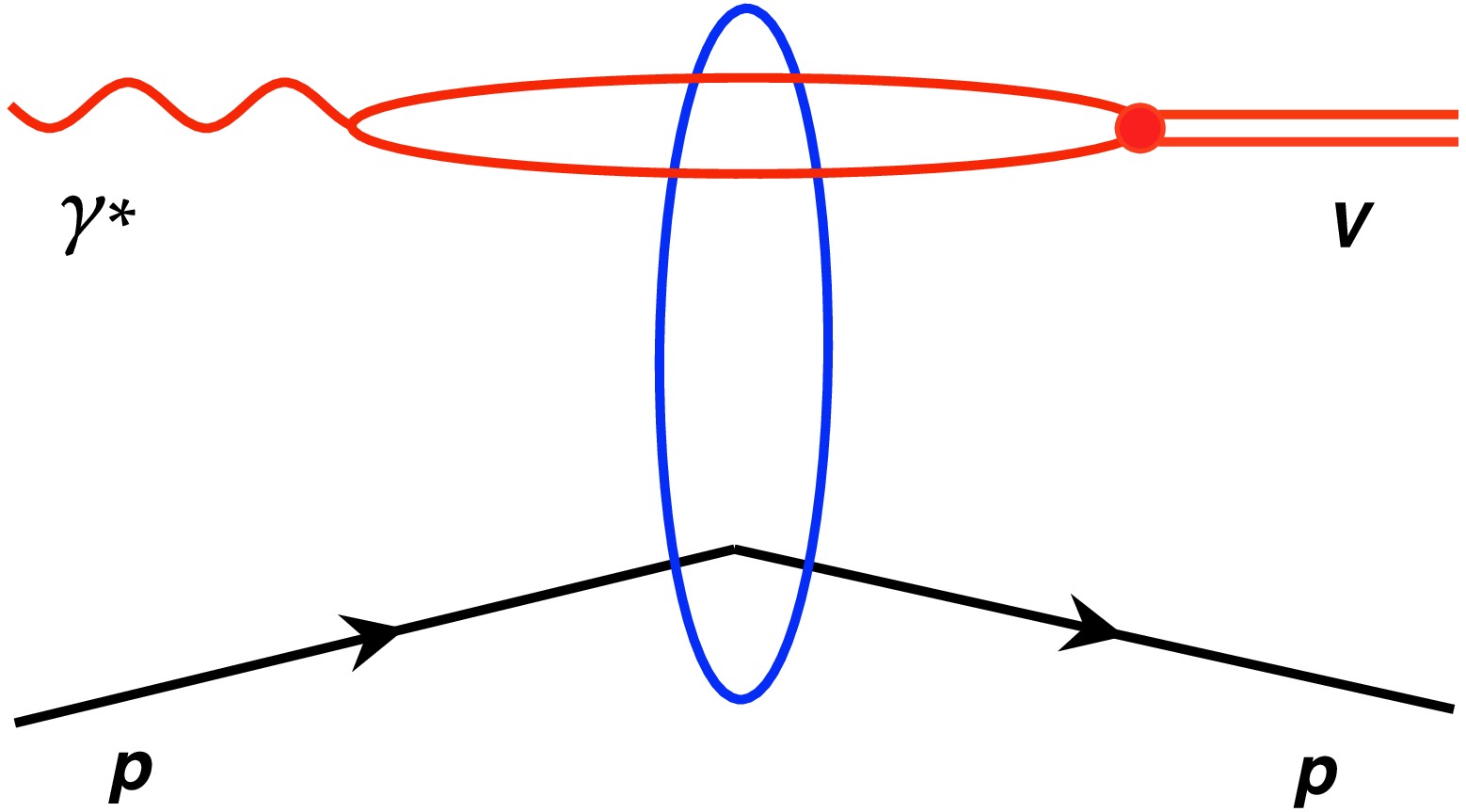

Figure 1.  (color online) The vector meson production process in a virtual photon-proton DIS is described in the dipole representation.

where T and L denote the transverse and longitudinal polarizations of the virtual photon, $ \mathit{\boldsymbol{r}} $ represents the transverse size of the $ q\bar{q} $ dipole, $ \mathit{\boldsymbol{b}} $ denotes the impact parameter of the dipole with respect to the proton target, and $ \mathit{\boldsymbol{b}} - (1/2-z)\mathit{\boldsymbol{r}} $ is Fourier conjugate to the momentum transfer $ {{\Delta}} $. The z in Eq. (3) is the longitudinal momentum fraction of the quark. The $ (\Psi_{V}^*\Psi_\gamma)_{T,L} $ is the overlap wavefunction between the virtual photon and vector meson, which is given by [2]

where e and $ \hat{e}_f $ are the charge and effective charge; for $ J/\Psi $, $ \hat{e}_f= 2/3 $. $ N_c $ is the number of colors. The $ m_f $ and $ M_V $ are the masses of the quark and vector meson, respectively. The $ K_0 $ and $ K_1 $ in the above equations are the modified Bessel functions of the second kind, where we define $ \epsilon^{2}=m_f^2+z(1-z)Q^{2} $. The $ \phi_T(r,z) $ and $ \phi_L(r,z) $ are the transverse and longitudinal scalar functions, which can be modeled in several ways. Currently, the most popular modeled scalar functions in the literature are the Boosted Gaussian [12, 13], Gauss-LC [14], and NRQCD [15] wave functions. It is known that the aforementioned scalar functions provide quite similar descriptions of the vector meson production data at HERA [2]. The main difference in the descriptions between the scalar functions lies solely in the normalization factor. Therefore, we choose to use the Boosted Gaussian wave function in this study. The Boosted Gaussian scalar functions are written as [2]

where $M_V=3.097 \mathrm{GeV}$, $m_f=1.4 \mathrm{GeV}$, $\mathcal{N}_{T}=0.578$, $\mathcal{N}_{L}= 0.575$, $\mathcal{R}_{T}=2.3$, and $\mathcal{R}_{L}=2.3$ for $J/\Psi$ production.

The dipole cross section, ${\rm d}\sigma^{\mathrm{dip}}/{\rm d}^2\mathit{\boldsymbol{b}}$, in Eq. (3) is a key ingredient, as it reflects the QCD interaction process between the $q\bar{q}$ dipole and the proton target. The dipole cross section can be expressed in terms of the optical theorem as

where N is the forward dipole scattering amplitude. It is well-known that the energy (rapidity) evolution of N obeys the Balitsky-JIMWLK equation [16−20]. In the mean-field approximation, the Balitsky-JIMWLK equation can be reduced to the closed Balitsky-Kovchegov (BK) equation [16, 21]. The BK equation is a differential-integral equation, making it very complex and not solvable analytically, although there are some approximate solutions in the saturation region [22, 23]. The numerical solutions of the BK equation are available in the literature [24, 25]. However, there are some tensions in the impact-parameter-dependent numerical solutions due to the Coulomb tail at large impact parameters [26, 27]. It is known that the impact parameter is an indispensable ingredient in probing the geometric structure of the proton through N. Thus, a mature model is necessary to describe the rapidity and impact parameter dependence of N. The IPsat model [14] is the desired one, providing successful descriptions in both inclusive and exclusive data at HERA. In the IPsat model, N can be written as

where $ xg(x,\mu^2) $ is the gluon density evolved with the LO DGLAP evolution equation. The scale μ in Eq. (9) is defined as

and the initial gluon distribution $ xg(x,\mu^2) $ at the scale $ \mu_0^2 $ is taken to be

with the model parameters $ \mu_0 $, $ A_g $, and $ \lambda_g $ taken from Ref. [28] in this work. The $ T_p $ in Eq. (9) is the proton profile function, which includes the spatial information of the proton. In the IPsat model, it takes a Gaussian distribution

with $ \mathrm{B_p} $ being the proton width.

Note that the above-mentioned proton profile function doesn't consider the influence of the event-by-event fluctuations. It is well known that the proton shape fluctuations have a great impact on the diffractive vector meson production, especially for the incoherent process [7, 29]. It has been found that the incoherent cross section of the $ J/\Psi $ production at HERA is underestimated by several orders of magnitude when the fluctuations are not included in the calculations. Inspired by the constituent quark picture, the HSM includes the fluctuations by assuming that the position of the constituent quarks and the density profile of each constituent quark vary from event to event. The HSM can give a reasonable description of the incoherent cross section of the $ J/\Psi $ production at HERA. However, the HSM cannot reproduce the coherent cross section of the $ J/\Psi $ production at relatively large $ |t| $ regions. In this work, we shall investigate the possible position distribution of the constituent quarks on top of the HSM, which will solve the issue of the HSM and improve the predictive power of the CGC effective theory.

Inspired by the constituent quark picture of the proton, the event-by-event fluctuations of the proton can be implemented in the following way. Firstly, the positions of each constituent quark in a proton fluctuate event-by-event, so we sample the quark positions ($ \mathit{\boldsymbol{r}} $) from Gaussian or exponential distributions,

or

where $ \mathrm{B_{qc}} $ and $ \mathrm{\tilde{B}_{qc}} $ are width parameters. Note that in this study, we neglect all possible correlations between the constituent quarks and assume that the angular distributions of the constituent quarks are uniform.

Secondly, the large-x valence quarks are considered to be sources of the small-x gluons, which are emitted around the valence quarks and form the "hot spot". The density profile of each hot spot is assumed to satisfy the Gaussian

or exponential distribution

with $ \mathrm{B_q} $ and $ \mathrm{\tilde{B}_q} $ being width parameters, where the subscript $ \mathrm{q} $ denotes quark flavor; $ \mathrm{q} $ can be up (u) or down (d) quarks, respectively. Thus, the profile function of the proton in Eq. (9) is the summation of the hot spots' density profiles,

where $ N_{hs} $ is the number of hot spots, and $ \mathit{\boldsymbol{b}}_i $ is the distance between the valence quark and the origin in the transverse plane.

In the HSM, the authors in Ref. [8] naively assumed that both the positions of the constituent quarks and the density profile of each hot spot obey Gaussian distributions (Eq. (13) and Eq. (15)), since the purpose of that work was to demonstrate the existence of geometric shape fluctuation of the proton and the importance of shape fluctuations in incoherent vector meson production. In fact, their work paved the way for investigating and applying proton shape fluctuations in the field of heavy-ion collisions. However, we find that the positions of the constituent quarks in the proton do not simply follow a Gaussian distribution, especially in the relatively large $ |t| $ region. In this study, we go beyond the HSM and investigate $ J/\Psi $ production with combinations of position and density distributions, such as (13)−(15), (13)−(16), (14)−(15), and (14)−(16). See the next section for a detailed description of the hybrid combinations. In the next section, we will find that an exponential distribution of the constituent quark position is essential for the theoretical model to reproduce the currently available $ J/\Psi $ production experimental data in all $ |t| $ regions at HERA energy.

We present the numerical results on coherent (Coh) and incoherent (Incoh) differential cross sections of $ J/\Psi $ production from the modified HSM introduced in Section III at HERA energies. To demonstrate the enhancement of our modified HSM over the original HSM, we use two types of independent measurements from different collaborations at HERA to verify the improvement of our model. Therefore, we calculate the differential cross sections as a function of W at fixed $ |t| $, and as a function of $ |t| $ at fixed W, respectively.

We start by calculating the coherent $ J/\Psi $ production differential cross section as a function of W with the original HSM and our modified HSM. In this work, we take into account the distribution differences between the u quark-induced hot spots and the d quark-induced hot spot due to the differences in their mass and transverse momentum distribution [30]. So, we consider the cases: (i) the u-spots and d-spot share the same Gaussian (GAU) distributions, (ii) they share the same exponential (EXP) distributions, (iii) the u-spots have a Gaussian distribution while the d-spot obeys the exponential distribution. Moreover, we need to sample the positions of the constituent quarks. Combining the distributions of the position of the constituent quarks and hot spot density together, we take into account three groups of combinations: GAU-GAU-GAU ¹, EXP-EXP-EXP, and EXP-EXP-GAU, when the differential cross sections are calculated. We compare our numerical results with the HERA measurements at $ |t|=0.3 $, $ 0.675 $, $ 1.05 $, and $ 1.5\; \mathrm{GeV}^2 $ in Fig. 2. In Fig. 2, the blue curves denote the predictions computed by the HSM (GAU-GAU-GAU), while the red and black curves represent the results calculated by the modified HSM with the combinations EXP-EXP-EXP and EXP-EXP-GAU. Note that the model parameters are fixed by aligning the model calculations with the $ W=75\; \mathrm{GeV} $ data (upper left panel in Fig. 3) in this work. Then, we use these parameters to calculate the differential cross sections in other cases.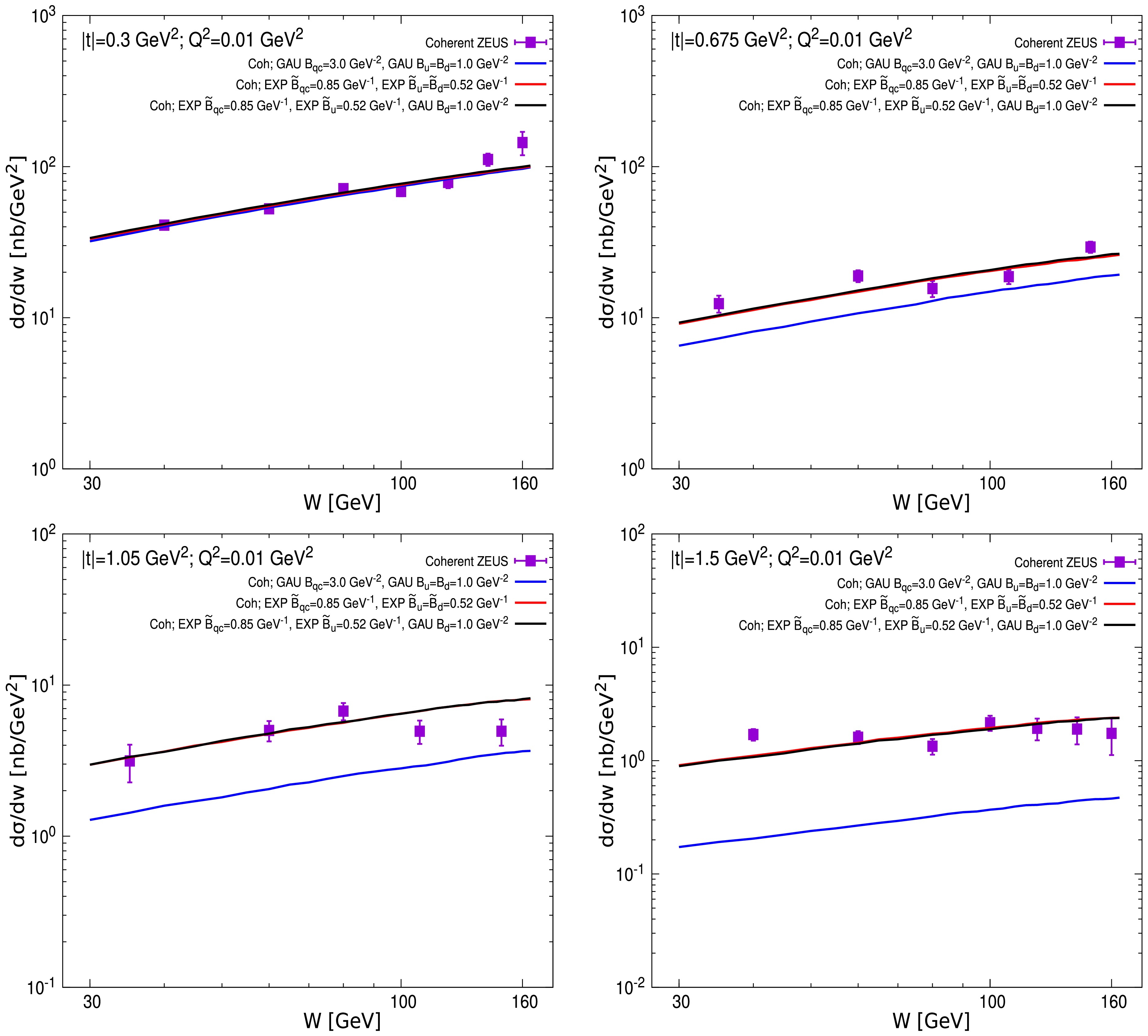

Figure 2.  (color online) The coherent $ J/\Psi $ production differential cross sections as a function of W at fixed $ |t| $ values, as compared to the data from the ZEUS collaboration [31].

Figure 3.  (color online) The coherent (solid curves) and incoherent (dashed curves) differential cross sections of $ J/\Psi $ production are presented as a function of $ |t| $ at $ \sqrt{s}=75 $, $ 80 $, $ 95 $, and $ 100\; \mathrm{GeV} $. The experimental data are sourced from Refs. [31, 33−37].

One can see that both the HSM and modified HSM can give a reasonable description of the HERA data at small $ |t| $, such as $ |t|=0.3\; \mathrm{GeV}^2 $ in Fig. 2. We would like to note that even better agreement is achieved when we compare our model calculations with HERA data in the case of $ |t|<0.3\; \mathrm{GeV}^2 $ (not shown here). By a global analysis of Fig. 2, we find that the HSM cannot reproduce the measurements at large $ |t| $. Specifically, the deviations between the HSM calculations and experimental data increase as $ |t| $ increases, see the blue curves in Fig. 2. Interestingly, it is shown that if the position distribution of the constituent quarks is changed from the Gaussian distribution to the exponential distribution in the modeling, the results are in agreement with the measurements across the entire available $ |t| $ region at HERA, regardless of what distribution function is used for the hot spot density profile, see the red and black curves in Fig. 2. It is worth pointing out that we also compute the coherent cross-section in the case with a fixed exponential distribution of position, but by flipping the u-spot and d-spot distributions, we obtain almost the same results as the black curves. All the above outcomes indicate that the position distribution function of the constituent quarks is a key factor in describing the $ J/\Psi $ production data at relatively large $ |t| $, and hints at a possible exponential distribution of the constituent quarks within the proton at high energy.

Currently, the largest available $ |t| $ data in the coherent process at HERA are around $ 1.5\; \mathrm{GeV}^2 $. It is known that at large values of $ |t| $, the dominant process in vector meson production is the incoherent process in which the proton becomes excited and finally dissociated in the scattering. Fortunately, the near-future electron-ion collider (EIC) has higher luminosity and wider acceptance [32], which can provide unprecedentedly higher precision and larger $ |t| $ data in the forward rapidity regions. Thus, one can use these data to further constrain the position distribution of the constituent quarks.

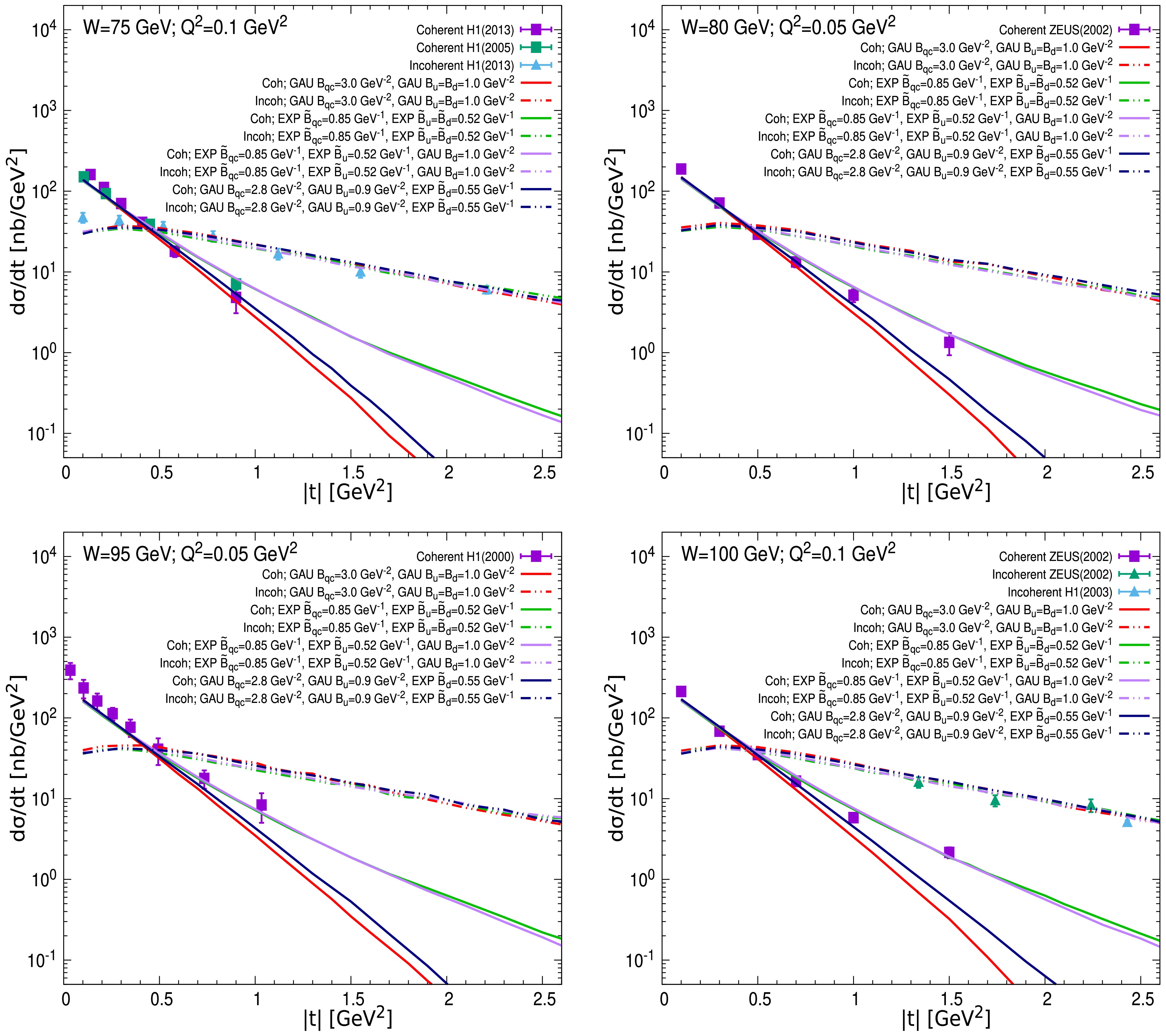
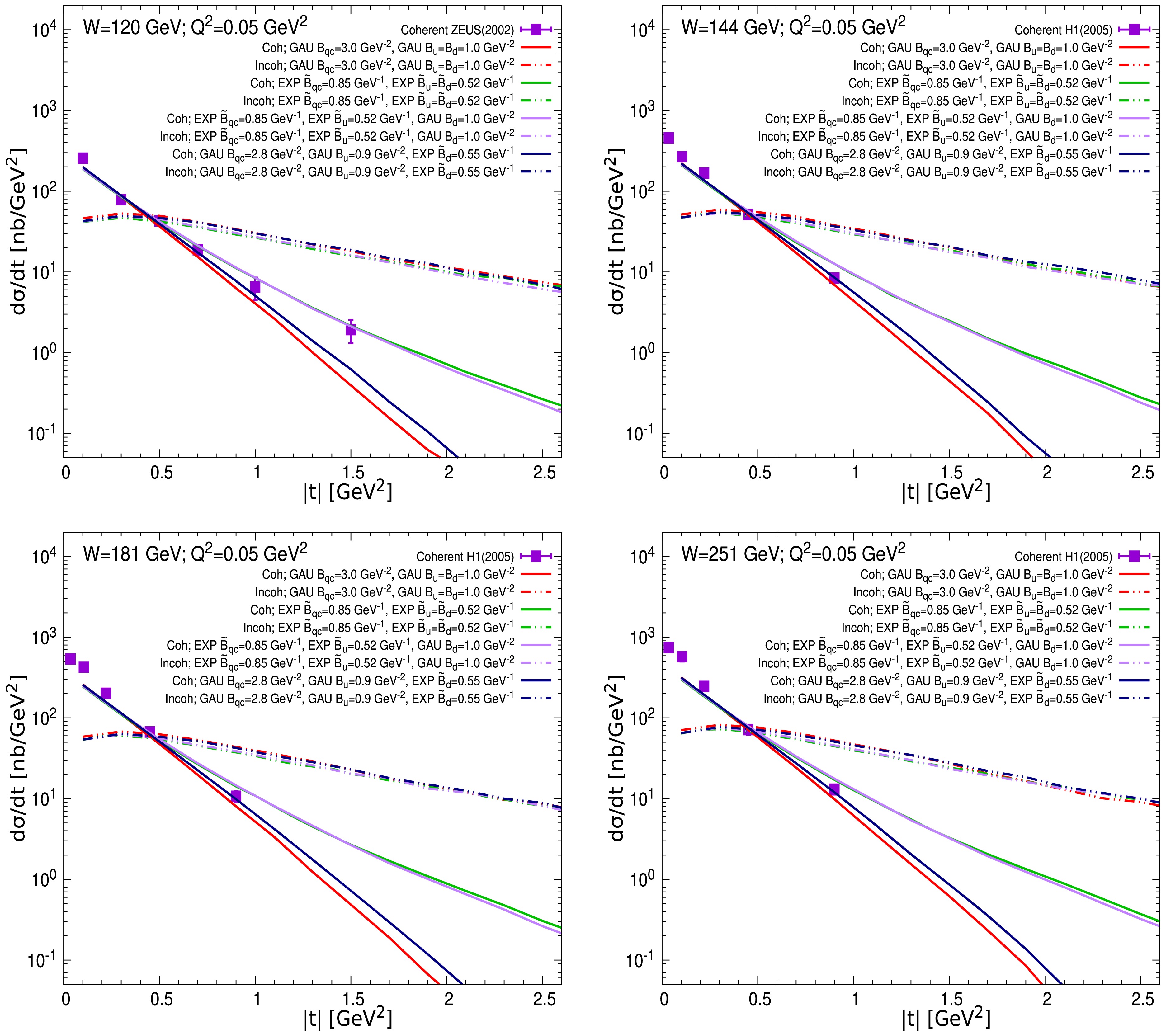
The differential cross sections as a function of $ |t| $ are calculated by the original HSM and our modified HSM. Comparisons to the H1 [33−35, 37] and ZEUS [31, 36] data on coherent and incoherent diffractive $ J/\Psi $ production at $ <W>=75, \; 80,\; 95,\; 100,\; 120,\; 144,\; 181 $, and $ 251 $ GeV, corresponding to highest and lowest $ x=1.7\cdot10^{-3} $ and $ x=1.5\cdot10^{-4} $, are shown in Figs. 3 and 4. Here, we consider four different combinations for the position distributions of the constituent quarks, u-spots and d-spot density in the computations, such as GAU-GAU-GAU, EXP-EXP-EXP, EXP-EXP-GAU, and GAU-GAU-EXP, which correspond to the red, green, purple, and blue curves. From the upper left and lower right panels of Fig. 3, one can see that all the results (dashed curves) of the incoherent cross section from four combinations are in agreement with the HERA measurements in the entire $ |t| $ region, which suggests that one cannot use the incoherent process to probe the position distribution of the constituent quarks. We also compute the incoherent cross sections at other energies where there are no relevant HERA data, see Figs. 3 and 4. Although there are no data points to directly distinguish the differences between the results obtained under the four combinations, one can still infer that the incoherent process cannot provide much information about the position distribution of the constituent quarks within the proton. We would like to note that the saturation scale ($ Q_s $) fluctuations are considered in our calculations in order to obtain a reasonable description of the incoherent $ J/\Psi $ production data at very small $ |t| $. The detailed calculations of the $ Q_s $ fluctuations are not shown here, as they are outside the interest of this work. For a pedagogical discussion of the $ Q_s $ fluctuations within the HSM, we refer the reader to Ref. [8].

Figure 4.  (color online) The coherent (solid curves) and incoherent (dashed curves) differential cross sections of $ J/\Psi $ production as a function of $ |t| $ at $ \sqrt{s} = 120 $, $ 144 $, $ 181 $, and $ 251\; \mathrm{GeV} $ are shown. The experimental data are taken from Refs. [31, 34].

Apart from the results of the incoherent cross section, we also present our predictions for the $ J/\Psi $ production in the coherent process in Figs. 3 and 4. It is shown that the results from the four combinations of distributions are consistent with the HERA data at all energies for $ |t|<1.0\; \mathrm{GeV}^2 $, indicating that the coherent process at very small $ |t| $ also cannot be used to probe the position distribution of the constituent quarks. When the $ |t| $ becomes large ($ |t|>1.0\; \mathrm{GeV}^2 $), the differences between results calculated by the Gaussian and exponential distributions of constituent quarks start to emerge, and differences increase as $ |t| $ increases. This shows that the predictions computed by the Gaussian position distribution of the constituent quarks (including results from the HSM, red curves) cannot reproduce the HERA measurements, as seen in the right panels of Fig. 3 and the upper left panel of Fig. 4. In contrast, the coherent cross sections calculated by our modified HSM can successfully reproduce the HERA data, which indicates that the position of the constituent quarks may obey an exponential distribution at high energy. This also means that the coherent process can be an effective probe to investigate the position distribution of partons within the proton.

Finally, it is worth pointing out that we use measurements from two independent aspects, t-dependence of the cross section in this subsection IV.B and W-dependence of the cross section in the above subsection IV.A, to cross-check the reliability of our outcome. All the calculations show that the position of the constituent quarks in the proton may obey an exponential distribution rather than a Gaussian distribution at high energy.

Deciphering the proton's internal structure is still one of the major challenges in the field of high energy physics. Remarkable progress has been achieved in understanding this subject over the past few decades, associated with the Color Glass Condensate effective theory, a mass of high precision HERA data, and the forthcoming electron-ion collider. The proton shape fluctuations have been identified through the HSM, which was developed based on the Color Glass Condensate theoretical framework. In this paper, we have performed an exploratory study on the position distribution of constituent quarks in the proton. We modify the HSM, which naively assumes both the position of the constituent quarks and the density profile of hot spots obey a Gaussian distribution, by introducing new distributions for the positions and hot spot densities. In all $ |t| $ regions, it shows that the modified HSM calculations can successfully reproduce both the W-dependent and t-dependent differential cross sections of $ J/\Psi $ production measured at HERA, which resolves the issues encountered in the HSM, specifically that the HSM cannot describe the coherent $ J/\Psi $ production data at relatively large $ |t| $. We also find that the description of the coherent cross-section of $ J/\Psi $ production remains robust when modeling the constituent quark positions with an exponential distribution, independent of the particular distribution function selected for the hot spot density profiles. These outcomes hint that the position of the constituent quarks in the proton may obey an exponential distribution rather than a Gaussian distribution at high energy.

In this paper, we assume that the up and down quarks obey the same position distribution although their triggered hot spots are treated individually. It is shown by a recent lattice QCD study that the density profile of the constituent quark has flavor dependence [38], which suggests that the position distribution of the constituent quark may also exhibit flavor dependence. This inspires us to further investigate the fine structure of the proton by considering the flavor dependence of the position distribution of the constituent quarks and the flavor dependence of their induced hot spots in future work.