-
During the last three decades, extensive study of nuclear multifragmentation has been conducted due to its possible link with the liquid-gas phase transition in nuclear matter [1-25]. This is considered due to the similarity between the nuclear forces and Van der Waal's interactions, i.e., a long range attractive part and short range repulsive core. The first effort in this regard was the Fermi-lab-Purdue experiment on the reactions of p+Kr and p+Xe systems. The mass yield of fragments of up to mass 30 was fit with a power law dependence (
$ Y(A_f)\propto A_{f}^{-\tau} $ ) [19]. This observation is consistent with the prediction of Fisher's droplet model, and it stimulated a large number of studies on the topic. The incident energy at which the liquid-gas phase transition occurs is often labeled as the "onset of multifragmentation" or "critical energy point" [4-9, 14-21, 23].Generally, the charge (or mass) yield of fragments is fit with a power law
$ \propto Z_{f} ^{-\tau} $ (or$ A_{f} ^{-\tau} $ ), and the value of τ is extracted [4-7, 9, 11, 14-17]. The minima of the τ value, when plotted as a function of the incident energy, are assumed to indicate the onset of multifragmentation or the critical energy point [4-6, 9-11, 14-17]. Among the studies on this topic, Ogilvie et al. [9] performed an experiment with the ALADIN forward spectrometer at GSI, Germany and reported the existence of minima in the values of τ for Au induced reactions with C, Al, and Cu targets at an incident energy of 600 MeV/nucleon. Subsequently, Li et al. [15] performed an experiment using the Michigan State University (MSU) 4$ \pi $ -array to study the central reactions of 40Ar+45Sc. They reported a minimum in the power law exponent τ at 23.9 MeV/nucleon. However, the corresponding Percolation model calculations predicted a minimum value of around 28 MeV/nucleon [15]. In contrast, William et al. [3] reported the absence of minima in the values of τ for the highly charged colliding system of 84Kr+197Au at incident energies between 35 MeV/nucleon and 400 MeV/nucleon. The dominance of the Coulomb forces was thought to hinder the occurrence of such minima. Gupta and Pan have also reported similar results for 197Au+197Au reactions [26].In addition to minima in the values of τ, the use of other characteristic signals has also been advocated for the study of the onset of multifragmentation or the liquid-gas phase transition [5, 21-23, 27-31]. Among these are the fluctuation in the size of the largest fragment [27], the size of the second largest fragment [28], the asymmetry in the size of the two largest fragments [29], the parameters based on the moments of the charge distribution, i.e.,
$ S_2 $ ,$ \gamma_2 $ [21, 22], the bimodality of the order parameter [30, 31], the multiplicity derivatives [23] and the information entropy (H) [5], and Zipf's law [5]. Many studies have been performed using these signals, and great progress has been made on the theoretical and experimental fronts on the topic of liquid-gas phase transitions [5-8, 11, 18, 20, 23, 32]. See Refs. [1, 2, 33] for reviews on this topic.In the literature, there have been studies in which many-body dynamical models were used to investigate the liquid-gas phase-transition in nuclear matter, e.g., Ma et al. studied the reactions of 40Ar+27Al between 25 and 150 MeV/nucleon and found a minimum of τ at 65 MeV/nucleon using the Quantum Molecular Dynamics (QMD) model [4]. Belkacem et al. have analyzed the experimental data of the MULTICS-MINIBALL collaboration to investigate the reactions of 197Au+197Au at 35 MeV/nucleon, and they also presented theoretical calculations using the Classical Molecular Dynamics (CMD) model [18]; they obtained critical behavior in both the theory and experiment. Ma et al. studied 40Ar on 27Al,48Ti, and 58Ni reactions using the Neutron Ion Multi-detector for Reaction Oriented Dynamics (NIMROD) experimental set up [6-8] and also presented calculations using the CMD model [6, 7]. In their studies, they used most of the characteristic signals mentioned above and found critical behavior for the systems. However, two of the authors of the present study and collaborators reported no minimum in the power law exponent or clear onset of fragmentation in the reaction of 40Ar+45Sc using the Isospin dependent Quantum Molecular Dynamics (IQMD) model [10]. A minimum was obtained when the Coulomb potential was neglected [11].
The common point among the above mentioned studies using dynamical models is that all used the Minimum Spanning Tree (MST) algorithm to clusterize the phase space. Recently, we used various extensions of the MST method (which includes momentum and binding cuts) and found that there is no effect of these extensions [32] on the extraction of the minimum of the exponent τ for the reaction of 40Ar+45Sc. The absolute values were, however, far from the experimental data. To resolve the general problems of the MST algorithm, Puri and Aichelin [34] proposed the Simulated Annealing Clusterization Algorithm (SACA) [35, 36] based on the method of Dorso et al. [34]. This algorithm was found to resolve the reported failure of the MST method for weakly excited systems [36, 37]. Recently, two of the authors of the present study applied the QMD+SACA model to experimental data near the Fermi-energy domain and were successful in the effort [38]. The aims of the present study are two-fold: 1) to confront the QMD+SACA model with experimental data at and farther away from the Fermi energy domain for lighter, i.e., 40Ar+45Sc, and heavily charged systems, i.e., 84Kr +197Au, and 2) to determine whether combining various signals of the liquid-gas phase transition in the framework of the QMD+SACA model provides a consistent picture and/or to determine which signals are best suited for the purpose. The present calculations also consider the utilization of Zipf's law, which has been introduced as a possible signal of the liquid-gas phase transition but has been reported to show signatures at much higher excitation energies, as shown in Refs. [20, 39]. Our study includes lighter systems of 40Ar+45Sc and heavier systems of 84Kr +197Au. Note that the main difference is not only the size of the system but also the larger Coulomb forces in the latter compared to those in the former. The study reveals whether the involvement of these large Coulomb forces influences the compatibility of the QMD+SACA model.
In Section 2, we briefly discuss both the primary and secondary models. A detailed analysis of the theoretical calculations is given in Section 3. Finally, we summarize our findings in Section 4.
-
The quantum molecular dynamics [40] model is a many-body dynamical model that simulates heavy-ion collisions on an event-by-event basis. In this model, the time evolution of a reaction is studied by following individual nucleons. The trajectories of nucleons during the reaction are determined by mean field and nucleon-nucleon collisions. The model describes the reaction from the well separated target and projectile up to the freeze-out (final) stages, in which the nuclear matter is fragmented. In this model, each nucleon of two colliding nuclei is represented by a Gaussian wave packet in the position and momentum space as [40]
$ \psi_{i}({{{r}}},{{{p}}}_{i}(t), {{{r}}}_{i}(t)) = \dfrac{1}{(2\pi L)^{\frac{3}{4}}}\; {\rm e}^{ [ \frac{i}{\hbar} { {{p}}}_{i}(t)\cdot{{{r}}}-\frac{({{{r}}}-{{{r}}}_i(t))^2}{4L}]}. $

(1) To build a nucleus, the coordinates are assigned to nucleons inside a sphere of radius R
$ = 1.142 A^{1/3} $ (where A is the mass number of the nucleus) in accordance with the liquid drop model. The nucleons are also assigned Fermi-momentum values between 0 and$ P_{\rm F} $ . Here,$ P_{\rm F}(r_i) $ =$ \sqrt{2mV(r_i)} $ with V($ r_i $ ) being the local potential energy of the$ i^{\rm th} $ nucleon. If the chosen momentum leads to an overlap in the phase space with any previously defined nucleon, the configuration is rejected. To keep the QMD formulation as close as possible to classical transport theory, the Wigner densities are used instead of the wave functions. The Wigner densities correspond to the phase-space densities in classical mechanics. The Wigner representation of the$ A_T + A_P $ nucleon system is given by$ f({{r}}, {{p}}, t) = \displaystyle\sum_i \dfrac{1}{(\pi \hbar)^3} {\rm e}^{-[{{r}}-{{r}}_i(t)]^2/2L-[{{p}}-{{p}}_i(t)]^2 2L/\hbar^2}. $

(2) The Wigner representation of the Gaussian wave packets obeys the uncertainty principle, and the one body densities in coordinate and momentum space are given by
$ \rho ({{r}},t) = \int f({{r}}, {{p}}, t) {\rm d}^3 {{p}} =\displaystyle\sum_i \frac{1}{(2 \pi L)^{3/2}} {\rm e}^{-[{{r}}-{{r}}_i(t)]^2/2L}, $

(3) $ g({{p}}, t) = \int f({{r}}, {{p}}, t) {\rm d}^3 {{r}}. $

(4) For each nucleus generated by the above procedure, the ground state properties, such as the binding energy and nuclear density, are checked. If a nucleus fulfills these conditions, then it is said to be successfully initialized. The successfully initialized target and projectile are boosted towards each other. During the reaction, the centroid of each Gaussian propagates using the classical equations of motion:
$ \begin{array}{l} \dot{{{{r}}}}_i = \dfrac{\partial H}{\partial{{{p}}}_i}, \;\;\;\;\; \dot{{{{p}}}}_i = -\dfrac{\partial H}{\partial{{{r}}}_i}, \end{array} $

(5) where H represents the Hamiltonian and is given by
$ \begin{aligned}[b] \langle H\rangle = \langle T\rangle+\langle V \rangle =& \sum_{i}\frac{p^{2}_{i}}{2m_{i}} + \sum\limits_{i}\sum\limits_{j>i}\int f_{i}({{r}}_{i},{{p}}_{i},t) {V_{ij}} ({{r}}_{i},{{r}}_{j}) \\ & \times f_{j}({{r}}_{j},{{p}}_{j},t) {\rm d}{{r}}_{i} {\rm d}{{r}}_{j} {\rm d}{{p}}_{i} {\rm d}{{p}}_{j}. \end{aligned} $

(6) Here,
$ f_i $ and$ f_j $ are the Wigner distribution functions of the i$ ^{\rm th} $ and j$ ^{\rm th} $ nucleons, respectively, and V$ _{ij} $ (${{r}} _{i} $ ,${{r}} _{j} $ ) is the baryonic interaction, which has as essential components the Skyrme, Yukawa, and Coulomb terms, and reads as$ \begin{array}{l} V_{ij} ({{r}}_{i}, {{r}}_{j}) = V_{ij}^{\rm Skyrme} + V_{ij}^{\rm Yukawa} + V_{ij}^{\rm Coulomb}, \end{array} $

(7) $ \begin{aligned}[b] V_{ij} ({ r}_i, { r}_j)=& t_1 \delta({{r}}_{i}-{{r}}_{j})+ t_2 \delta({{r}}_{i}-{{r}}_{j}) \rho^{\gamma-1} \left(\frac{{{r}}_{i}+{{r}}_{j}}{2}\right) \\ & + t_{3}\frac{\exp(-|({{r}}_{i}-{{{r}}}_{j})|/\mu)}{(|({{{r}}}_{i}-{{{r}}}_{j})|/\mu)} + \frac{Z_{i}Z_{j}e^{2}}{|{{{r}}}_{i}-{{{r}}}_{j}|}. \end{aligned} $

(8) Here,
${{t}} _1 $ and${{t}} _2 $ depend on the values of$ \alpha $ and$ \beta $ (described below),${{t}} _{3} $ and$ \mu $ are -6.66 MeV and 1.5 fm, respectively, and$ {{Z}}_{i} $ and$ {{Z}}_{j} $ denote the charges of the$ i^{\rm th} $ and$ j^{\rm th} $ baryons. In the limit of nuclear matter, the (two- and three-body) Skyrme interactions can be reduced to density dependent potential of the form$ U^{\rm Sky} = \alpha\left(\frac{\rho}{\rho}_o\right)+ \beta \left(\frac{\rho}{\rho}_o\right)^{\gamma}. $

(9) The parameters
$ \alpha $ and$ \beta $ are adjusted so that the average binding energy has a minimum at the normal nuclear matter density ($ {\rho}_o $ ) and should be equal to −15.76 MeV, while$ \gamma $ determines the compressibility. During the course of propagation, if the two nucleons come closer than$ {\sqrt{{\sigma_{NN}}/\pi}} $ , where$ \sigma_{NN} $ is the nucleon-nucleon cross-section, they suffer a collision. Here,$ \sigma_{NN} $ is the energy dependent nucleon-nucleon cross-section [40]. Before every collision, the nucleons are checked for Pauli blocking: if the phase space where the nucleons would go after scattering is already filled, the collision is neglected; otherwise, it is allowed. Within the framework of the QMD model, to calculate Pauli blocking, for simplicity, a sphere in coordinate and momentum space that corresponds to each nucleon is considered. In this way, it is possible to achieve the same Pauli blocking ratio that would be obtained for each Gaussian, for which the calculations take much longer. Here, we calculate the fractions P$ _1 $ and P$ _2 $ of the already filled final phase space, which will be occupied by scattered partners. Collisions are then blocked with probability$ \begin{array}{l} P_{\rm block} = 1-[1-{\rm min}(P_1, 1)][1-{\rm min}(P_2, 2)], \end{array} $

(10) and the corresponding collision is allowed with probability (1-
$ P_{\rm block} $ ). If a collision is blocked, the nucleons are assigned the same momenta that they had before the collision The reaction information, in the form of the phase space of the nucleons, is stored at various time steps during the propagation. For the nuclear matter incompressibility K = 200 MeV, the values of the parameters$ \alpha $ ,$ \beta $ , and$ \gamma $ are −356 MeV, 303 MeV, and 1.17, respectively. Using this soft equation of state coupled with the energy-dependent nucleon-nucleon cross-section, various experimental observations have been explained in previous studies [37, 38, 41-46]. -
It is now well known that as soon as nucleons leave the compression phase, clusterization algorithms, also known as secondary models, are evoked to obtain the fragments. We use the simulated annealing clusterization algorithm (SACA) [35, 36]. This method utilizes the concept of energy minimization via the simulated annealing technique to obtain the most bound fragment configuration. To exclude the formation of loosely bound clusters in intermediate stages of the algorithm, a binding energy cut is implemented on the
${{k}} ^{\rm th} $ cluster:$ \begin{aligned}[b] \zeta_k =& {\sum\limits_{i = 1}^{A_f}}\left[\sqrt{\left({{p}}_{i}-{{p}}^{\rm cm}_{A_f}\right)^2 + m^2_i} - m_i \right.\\&\left.+ \frac{1}{2}{\sum\limits_{j\neq i}^{A_f}}{V_{ij}({{r}}_i,{{r}}_j)} \right] < E_{\rm bind}\times A_f, \end{aligned} $

(11) with E
$ _{\rm bind} $ = - 4.0 MeV if A$ _{f} $ $ \geqslant $ 3, and E$ _{\rm bind} $ = 0 MeV otherwise. In the above equation, A$ _{f} $ and$ {{p}}_{A_f}^{\rm cm} $ represent the total number of nucleons in a fragment and the center-of-mass momentum of that fragment, respectively. It is worth mentioning that the potentials used in the above equation are the same as those used in the QMD model to maintain self-consistency. It has been previously shown that the exact values of the binding energies do not affect the most bound structures of the fragments [41]. In the absence of such conditions, fragments are still bound close to their true ground state binding energies as per the QMD model. Within the SACA method, the total binding energy of the clusters$ \zeta_{\{C_k\}} $ for cluster set$ \{C_k\} $ is calculated at each step:$ \begin{array}{l} \zeta_{\{C_k\}} = \displaystyle\sum\limits_k \zeta_k. \end{array} $

(12) After the initial configuration is obtained in the first stage, usually using the MST method, the exchange of individual nucleons is allowed in order to find the possible best configuration. A new cluster configuration is always accepted if it is more stable, i.e., if the sum of the binding energies of the clusters is greater than that of the previous configuration. Otherwise, an exponential probability is assigned to the new configuration. In this way, a large number of configurations can be built. In the later stages, a fragment exchange procedure is also applied in order to achieve the global most bound configuration. The iterations are terminated if the exchange of nucleons does not alter the sum of the binding energies of the clusters. After millions of iterations the most stable cluster configuration is accepted. For example, if we start from the ground state of the nuclei, i.e., 20Ne, 40Ca, 93Nb, and 208Pb, generated by the QMD model and then break them into a number of fragments, the SACA finds the same nuclei with ground state binding energy after nearly 8000, 12000, 62000, and 280000 iterations, respectively [36]. The reader is referred to Ref. [36] for the detailed procedure followed in the SACA.
In earlier studies, the SACA method was found to be exceptionally successful in reproducing experimental data for wide entrance channels [35-38, 41, 47, 48]. This method explains not only experimental observations such as the multiplicity of fragments and the size of the largest cluster but also the physics of event-by-event based observables such as multiplicity probabilities and probability distributions of the three largest clusters. The algorithm both identifies realistic fragment structures and realizes fragment structures as early as
$ \sim $ 60-90 fm/c, when the matter is still dense and hot. This time is much shorter than that required by the standard MST method to provide the final fragment structures ($ \sim $ 300 fm/c). In other words, the SACA also enables understanding of the reaction dynamics during the violent stages of a reaction. For more details about the SACA method, readers are referred to Refs. [35, 36]. -
For the present study, several thousand events of reactions of 40Ar+45Sc and 84Kr+197Au were generated at different beam energies (ranging between 15 MeV/nucleon and 400 MeV/nucleon). The reactions were simulated for a reduced impact parameter,
$ \hat{b} \leqslant $ 0.25; this choice was guided by previous studies [3, 15]. Here, the soft equation of state supplemented by the Cugnon parametrization of the nucleon-nucleon (NN) cross-section is used to simulate the above reactions [40]. It is worth mentioning that this choice of the equation of state and NN cross-section has been highly successful in explaining various experimental results [37, 38, 41-46]. -
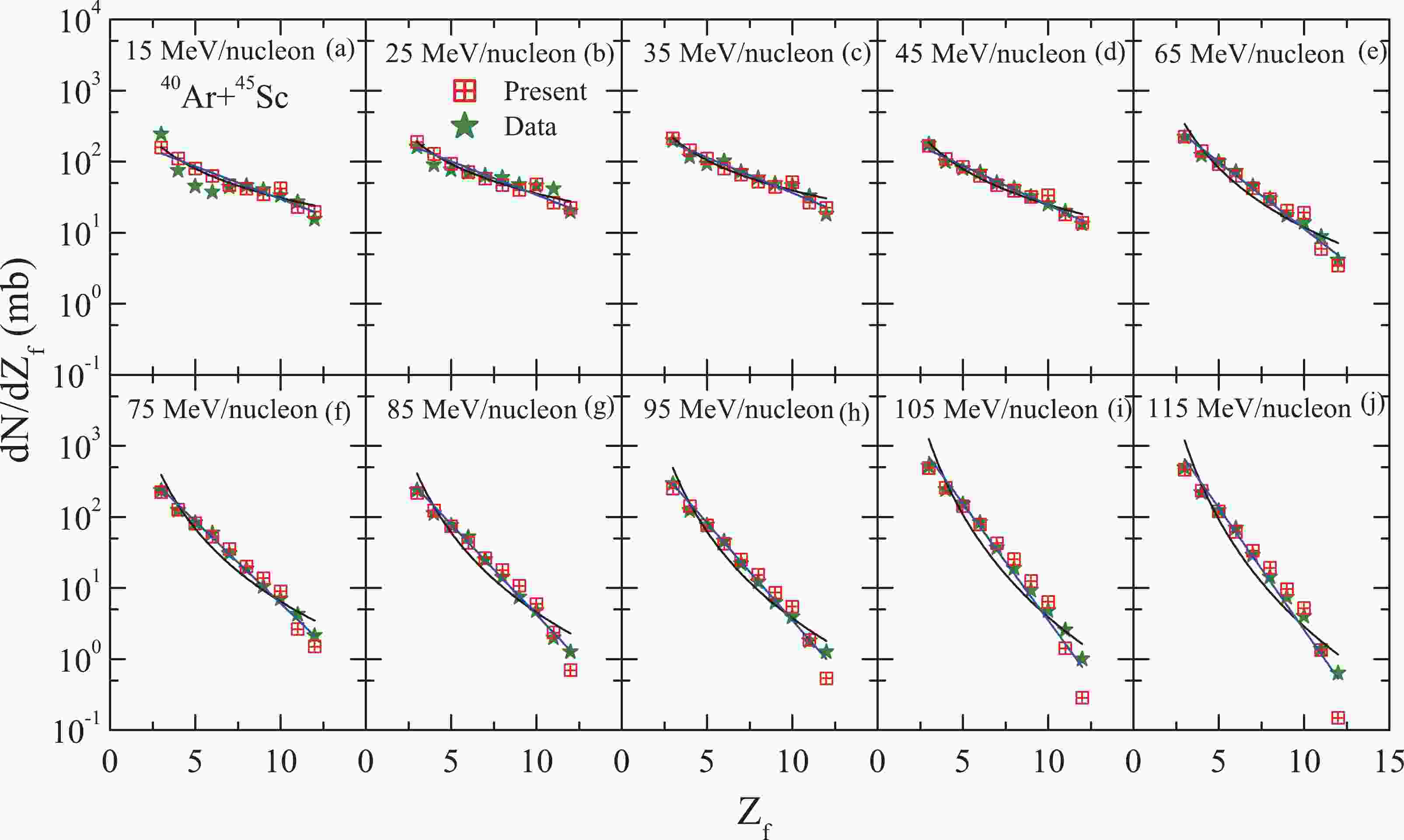
In Fig. 1, we display the charge yields (see the crossed squares) calculated using the QMD model coupled with the SACA method for central collisions (
$ \hat{b} \leqslant $ 0.25) of 40Ar+45Sc at different incident energies between 15 and 115 MeV/nucleon. The choice of the centrality and incident energy range was guided by experimental measurements reported in Ref. [15]. Along with the calculated yields, we also provide the available experimental data (see the stars) [15]. It can be observed that as one increases the incident energy of the projectile, the excitation energy of the composite system increases, and the yield of the heavier (lighter) fragments therefore decreases (increases). Hence, the slope of the charge yield becomes steeper with the incident energy, signifying the violence of the binary collisions. We observe that the results of QMD+SACA model reveal the same behavior, and that they are consistent with experimental results for intermediate mass fragments (IMFs),$ 3 \leqslant Z_f \leqslant 12 $ , and calculations reported in earlier studies [3, 4, 9-11, 13-15, 38, 47, 48]. Encouragingly, the QMD + SACA model can closely reproduce the measured charge yields at all incident energies, except at a few points at 15 MeV/nucleon. The discrepancy at 15 MeV/nucleon is due to slightly less appropriate Pauli blocking at this low incident energy [40]. In earlier studies, the charge distribution (for 3≤$ Z_{f} $ ≤12) was often fit with a power law$ \propto $ $ Z_f^{-\tau} $ to investigate the critical energy point of the possible liquid-gas phase transition. Hence, we also fit the calculated charge yields [3≤$ Z_{f} $ ≤12] with a power law$ \propto $ $ Z_f^{-\tau} $ .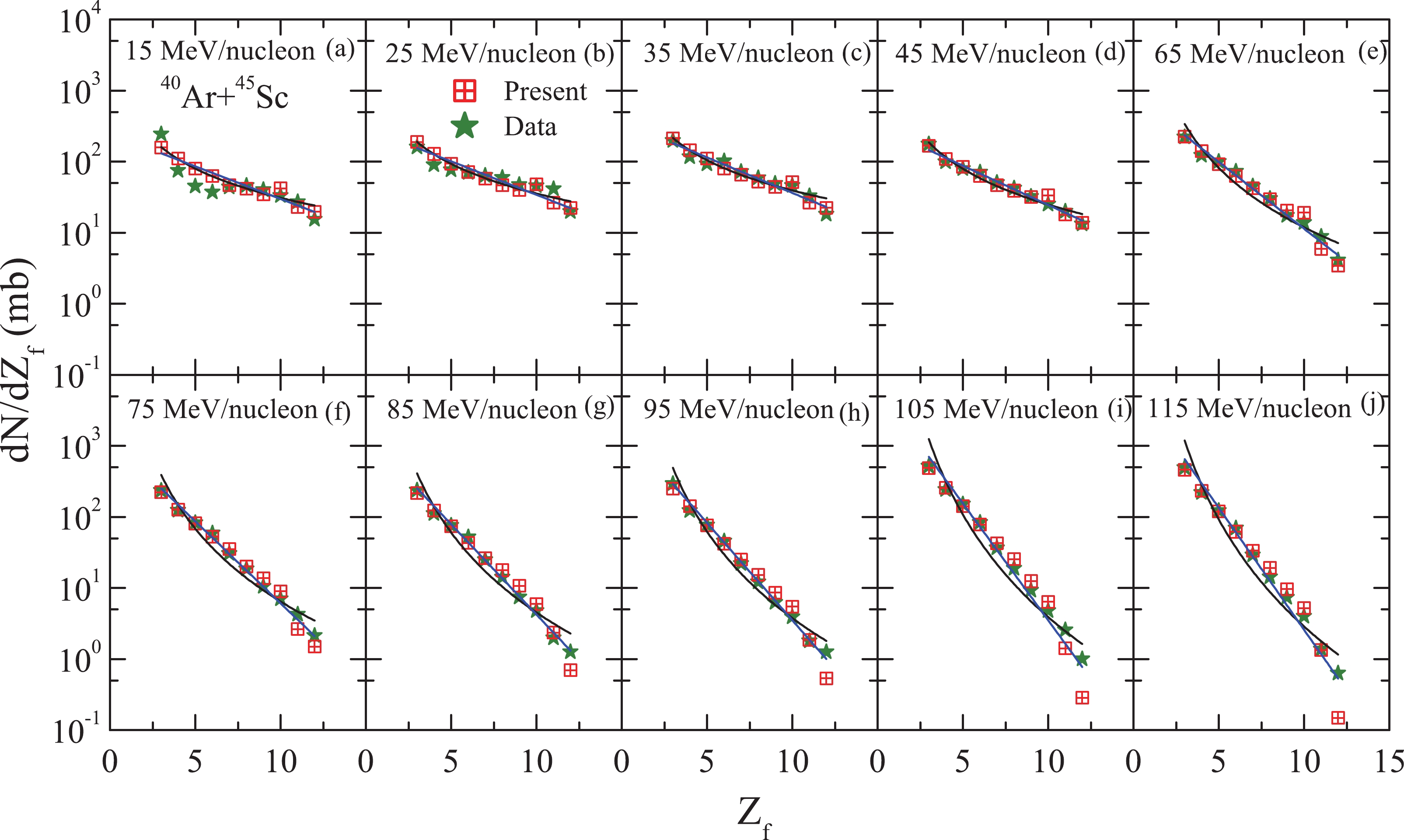
Figure 1. (colored online) Charge distributions obtained in the central reactions of 40Ar+45Sc at beam energies between 15 and 115 MeV/nucleon: The crossed squares show the calculated results of the QMD + SACA method, whereas the stars represent the experimental data [15]. The lines correspond to the power law and exponential fits of the fragment charge distributions for IMFs [3≤
$ Z_{f} $ ≤12] using the QMD + SACA model.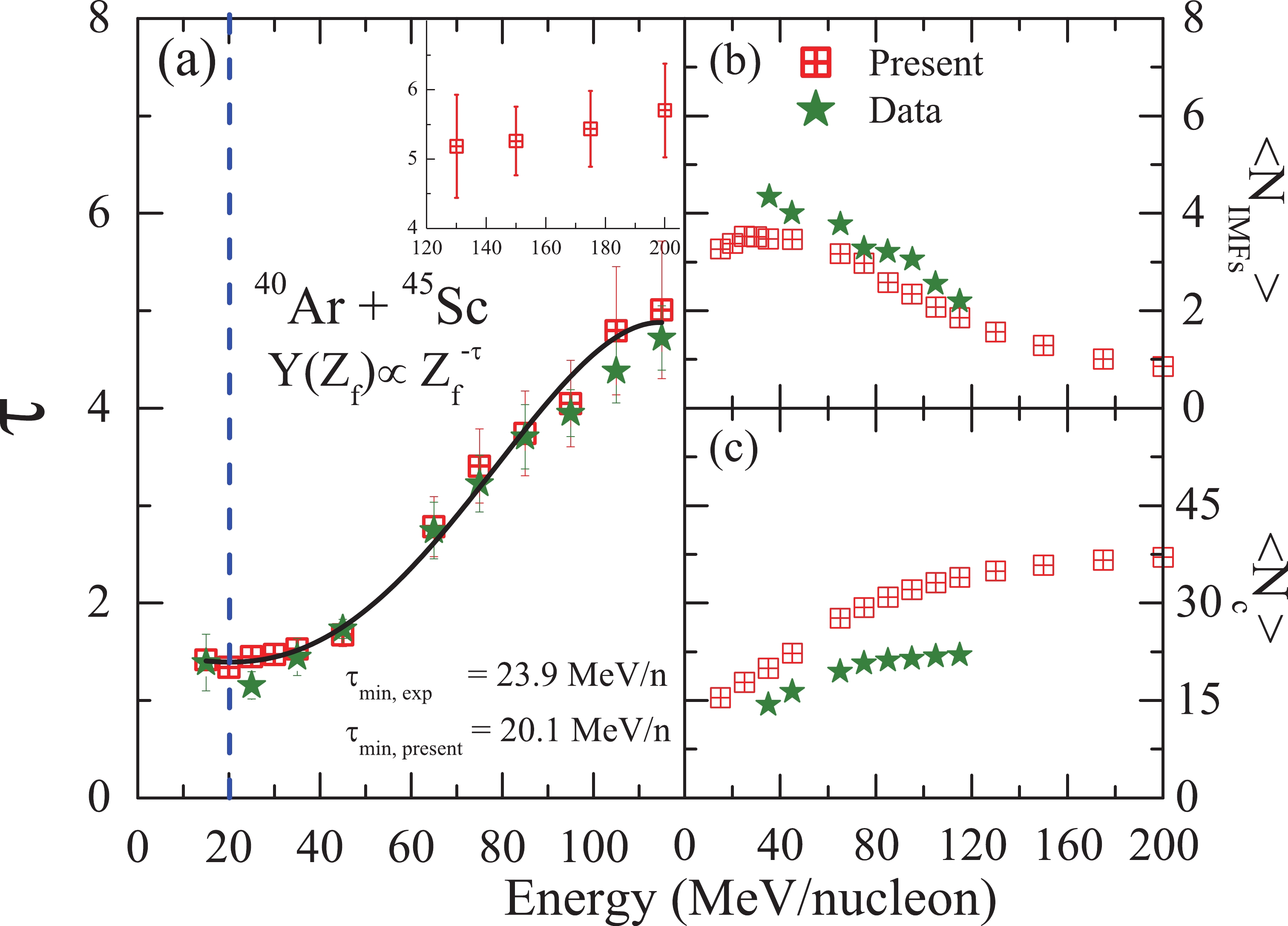
Figure 2. (color online) (left) The extracted values of the power law parameter τ (obtained from the power law fits
$ \propto $ $ Z_{f} $ $ ^{-\tau} $ of IMFs, as shown in Fig. 1) plotted as a function of the incident energy. The solid lines correspond to fourth order polynomial fits to the extracted τ values obtained using the QMD + SACA model. The dashed vertical line represents the point of onset of multifragmentation with the QMD+SACA model. (inset) We display the τ values in the incident energy range of 120 to 200 MeV/nucleon. (right) The multiplicity values of the IMFs ($ <N_{\rm IMFs}> $ ) and the charged particle multiplicity ($ <N_{\rm c}> $ ) are shown as functions of the incident energy of the projectile. The data points are taken from Refs. [14, 15], and the symbols have the same meaning as in Fig. 1.
Figure 3. (color online) The extracted values of the parameter
$ \lambda $ , obtained using exponential fits$ \propto $ e$ ^{-\lambda Z_{f}} $ of the IMFs. The normalized second moment$ <S_{2}> $ , variance$ <\gamma_{2}> $ , average charge of the second largest fragment$ <Z_{\rm max2}> $ , phase separation parameter$ S_p $ , and bimodality parameter P are plotted as functions of the incident energy. The dotted line shows the exact energy point of the onset of fragmentation.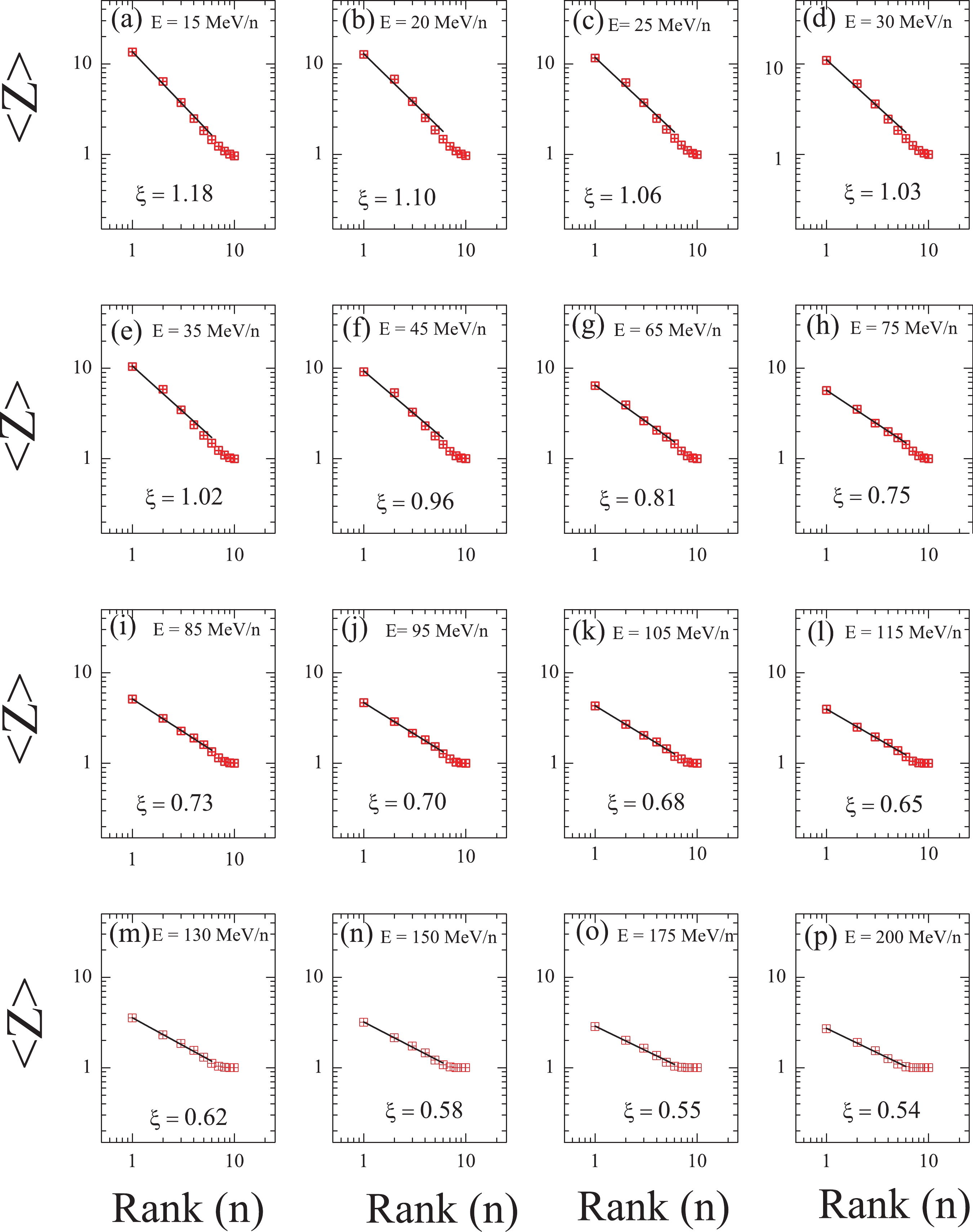
Figure 4. (color online) The values of
$ <Z> $ versus rank (n) in the decreasing order of the fragment charges at different incident energies for 40Ar+45Sc reactions. The lines denote the power law fit,$ <Z_n>\propto n^{-\xi}. $ The extracted values of τ are plotted in Fig. 2(a). We display the experimental values of τ obtained using the power law fit for the charge yield of IMFs with stars and our theoretical predictions with squares. We can see that the value of τ increases with the beam energy (>20 MeV/nucleon), reflecting the steepening of the slope of the charge distribution with the incident energy. Experimentally, it was observed that the value of τ changes from
$ \tau \simeq $ 1.2 at 25 MeV/nucleon to$ \tau \simeq $ 4.72 at 115 MeV/nucleon. The corresponding excitation energy was observed to vary from 8 to 29 MeV/nucleon. The minimum value that is considered a signal of criticality was obtained at 23.9 MeV/nucleon with$ \tau \simeq $ 1.21 by fitting the τ values with a fourth order polynomial. We also fit the τ values obtained using the QMD+SACA model with a fourth order polynomial and observed a minimum in the extracted τ value at 20.1 MeV/nucleon with$ \tau \simeq 1.39 $ . It is also important to mention that one usually expects to have τ = 2.2 at the critical point, whereas here the obtained values are much smaller. This deviation is due to the exclusion of lighter particles ($ Z_f \leqslant 2 $ ) from the fit. It was shown in Ref. [49] that the τ values depend crucially on the choice of the mass/charge range that is fit to obtain them. Our present prediction for the minimum value of the light charged system of 40Ar+45Sc is in a close agreement with the measured one (23.9 MeV/nucleon) [15]. We also inspect$ \chi^{2} $ values: their minimum should be at the critical point, and they should be larger at other values. To check the goodness of fit, we also calculated$ \chi^{2} $ for the power law fit [26]. We obtained the minimum value at 20.1 MeV/nucleon, i.e.,$ \chi^{2} \sim $ 1.1, which reaches very high values at other incident energies. This indicates that the best fit is obtained at the critical energy point, which further supports our results. This is the closest value reported in the literature to date for any theoretical model. In contrast, the QMD + MST model predicted the minimum value at 18.03 MeV/nucleon, and the values of τ were far from the experimental values [12, 32]. The Percolation model calculations also predicted the energy of the critical point at 28 MeV/nucleon with τ = 1.5; these values are much higher than the experimentally observed values [15]. The QMD + SACA calculations thus not only reproduce the measured charge yields but also appropriately explain the behavior of the power law factor "τ" over the entire energy range. To observe the trends, we have also provided τ values from the QMD+SACA model for incident energies from 115 MeV/nucleon to 200 MeV/nucleon, for which experimental values are not available (see the inset of Fig. 2(a)). We find that the τ values continue to increase with the rise in incident energy. The bottleneck in the present calculations is that the SACA method recognizes stable fragment structures as early as$ \sim $ 60-90 fm/c. It can thus provide vital information for the hot and dense nuclear matter.In Fig. 2 (b-c), we also display the multiplicities of the intermediate mass fragments (IMFs) (
$ <{{N}}_{\rm IMFs}> $ ) and the charged particle multiplicities ($< {N}_{\rm c}> $ ) for the 40Ar + 45Sc system as functions of the incident energy. For these observables, the experimental observations are only available for incident energies$ \geqslant $ 35 MeV/nucleon [14]. We see that the theoretical calculations are consistent for$ < {{N}}_{\rm IMF}> ,$ which decreases in multiplicity value as the incident energy is increased. However,$< {{ N}}_{\rm c} >$ is predicted to be quite large compared to the experimental values. This larger value of$< {{N}}_{\rm c}> $ is due to the excess of lighter particles. The result for$ <{{N}}_{\rm c}> $ can be qualitatively reproduced by the QMD+SACA model.We also found that in some studies, the exponential fit
$ \propto $ e$ ^{-\lambda} $ $ ^{Z_{f}} $ is used instead of the power law fit [7, 8]. The critical exponent$ \lambda $ is also considered here to show the minimum near critical point. To check this, we also fit the above calculated yields (see Fig. 1, straight lines) with exponential fits of the form$ \propto $ e$ ^{-\lambda} $ $ ^{Z_{f}} $ and plotted the extracted$ \lambda $ values in Fig. 3 (a). Interestingly, the QMD + SACA method again found a minimum in the extracted$ \lambda $ values. The exact minimum was extracted by fitting the$ \lambda $ values with a fourth order polynomial. The minimum value 23.1 MeV/nucleon is very close to the one obtained using the power law fit (= 20.1 MeV/nucleon) and to the experimental value (= 23.9 MeV/nucleon). It is the first time that such close agreement between model and experimental results has been obtained. It is worth mentioning, however, that this fit is poor, and that the$ \chi^{2} $ is exceptionally large in this case (except at higher incident energies$ \geqslant $ 45 MeV/nucleon, where it decreases). This fit was only used for the case study considering earlier studies [7, 8]. We have also provided some values of$ \lambda $ for 115 MeV/nucleon to 200 MeV/nucleon to examine the trend (see the inset of Fig. 3 (a)). We see the same trends, i.e., a gradually increasing trend for$ \lambda $ as the incident energy increases. -
At the minimum of the critical exponent τ, the fluctuations reach their maximum, indicating the possibility that this is the point of the onset of multifragmentation or the critical point of the liquid-gas phase transition. Campi [21] was the first to exploit this feature and introduced powerful methods to characterize the critical behavior in fragmentation. These methods are based on the conditional moments of the asymptotic cluster charge distributions. Generally, the
$ k^{\rm th} $ moment of the cluster charge distribution is defined as$ \begin{array}{l} M_k = {\displaystyle\sum\limits_{{Z_{f}}\neq{Z_{\rm max}}}} {Z_{f}^{k}}\; {n}{(Z_{f})}, \end{array} $

(13) where
$ Z_{\rm max} $ is the charge of the largest fragment, and$ n(Z_{f}) $ is defined as the multiplicity of the fragment having charge$ Z_{f} $ in an event. The moments are calculated event-by-event and then averaging is performed across the events. The normalized second moment ($ S_{2} $ ) is defined as [21, 22]$ S_2 = \frac{{\sum_{{{Z_{f}}\neq{Z_{\rm max}}}} Z_{f}^2 \; n(Z_f)}}{{\sum_{{Z_{f}}\neq{Z_{\rm max}}}} Z_{f}\; n(Z_{f})}, $

(14) and
$ \gamma_{2} $ is constructed as$ \gamma_{2} = \frac {M_{2}M_{0}}{M_{1}^{2}}. $

(15) The parameters
$ <S_{2}> $ ,$ <\gamma_{2}> $ , and$ <Z_{\rm max2}> $ (averaged over a large number of events) should exhibit a peak at the incident energy, where the minimum value of the exponent parameter τ is obtained [4, 19-22, 28].In Fig. 3 (b-d), we display the average values of
$ <S_{2}> $ ,$ <\gamma_{2}> ,$ and$ <Z_{\rm max2}> $ as functions of the incident energy. We see that all these parameters pass through their maximal value over the incident energy. Interestingly, all the parameters$ <S_{2}> $ ,$ <\gamma_{2}> $ , and$ <Z_{\rm max2}> $ predict a maximum at 20 MeV/nucleon, which is again very close to the earlier predicted value using τ/$\lambda $ , i.e., 20.1 (23.1) MeV/nucleon. We also used other critical parameters, i.e., the phase separation parameter and bimodal parameter, which we discuss below. -
The phase separation parameter (
$ S_p = <Z_{\rm max2}>/ $ $ <Z_{\rm max}> $ ), which was introduced in the percolation model calculations, reaches a value close to 0.5 near the critical point [49]. Ma et al. also utilized this parameter and found consistent results for the extraction of the critical energy point in their experimental study [8]. Our results for this parameter using the QMD+SACA model are displayed in Fig. 3 (e). If we see our calculations, the value of$ S_p $ exhibits linear behavior with two different slopes above and below the incident energy of 20 MeV/nucleon. We see$ S_p $ = 0.52 at 20 MeV/nucleon. Therefore, the present QMD+SACA calculations indeed display the characteristic signal of this parameter.The other parameter used here is the bimodal parameter. It is based on bimodality, i.e., the observation of a double peaked distribution of the order parameter [30, 31]. Each component is supposed to represent a different phase and provides a definition of the order parameter that separates the two peaks. Accordingly, if the nuclear system is in the region of coexistence, the distribution of the probability of the order parameter is bimodal in nature. Borderie et al. [50] defined
$ Z_f $ = 12 as the limit between the liquid-gas phase at INDRA. They defined$ (\sum_{Z_i \geqslant 13} Z_i-\sum_{3\geqslant Z_i \leqslant 12} Z_i/\sum_{Z_i \geqslant 3}Z_i) $ as the order parameter. This may be intended to connect the density difference between the liquid and gas phases. Ma et al. [8] changed this limit between the two phases of the lighter system to$ Z_f $ = 3 ($ Z_f \leqslant $ 3 as a gas and$ Z_f \geqslant $ 4 as a liquid) and defined the bimodal parameter as$ P = \frac{\displaystyle\sum_{Z_i \geqslant 4} Z_i-\sum_{1\geqslant Z_i \leqslant 3} Z_i} {\displaystyle\sum_{Z_i \geqslant 1}Z_i}, $

(16) where P = 0 was the point of equal distribution of the charge in the liquid and gas phases. In Fig. 3 (f), we show the results for the bimodal parameter for the 40Ar+45Sc reactions as a function of the incident energy. We see a change in the slope occurring near 20 MeV/nucleon, which is the point of coexistence. Next, we analyze Zipf's law and the information entropy [5] for characteristic signals of phase-transition.
-
Zipf's law is well known in linguistics as a relationship between the frequency rank of English words and their frequency of use in the literature [51]. Y. G. Ma [5] introduced Zipf's law as a characteristic signal of the liquid-gas phase transition in heavy-ion collisions. In heavy-ion collisions, the law is utilized as follows. The clusters are first arranged in decreasing order of their charges in an event. The largest is assigned rank 1, the second largest rank 2, and so on. The obtained values of the size of the fragments of the n
$ ^{\rm th} $ rank, i.e.,$ <Z_n> $ , are fit with a power law in the form$ <Z_n> \propto n^{-\xi} $ , where$ \xi $ is the order parameter. At the critical energy point, Zipf's law is followed with$ \xi $ = 1 [5]. In Ref. [52], it was shown that Zipf's law is simply a consequence of the power law fit, and that it does not add further information. In Refs. [7, 8], Zipf's law is followed. In Refs. [20, 39], Zipf's law is followed away from the critical point. It is interesting to see the results of our calculations using the QMD+SACA model for Zipf's law.In Fig. 4, we display a graph of
$ <Z> $ versus rank (n) at incident energies ranging between 15 and 200 MeV/nucleon. The values obtained via the power law fit ($ \xi $ ) are also shown at the corresponding incident energies. Note that we only use the power law fit for n$ \leqslant $ 6. The obtained values of$ \xi $ are plotted in Fig. 5 (a) as a function of the incident energy. We see Zipf's law$ \xi $ = 1 is satisfied at$ \sim $ 35 MeV/nucleon. This energy is far from the critical energy point predicted by using other order quantities. Our results using the QMD+SACA model are same as those reported in Refs. [20, 39]. Therefore, within the QMD+SACA model, there is no consistent picture between Zipf's law and other characteristic signals.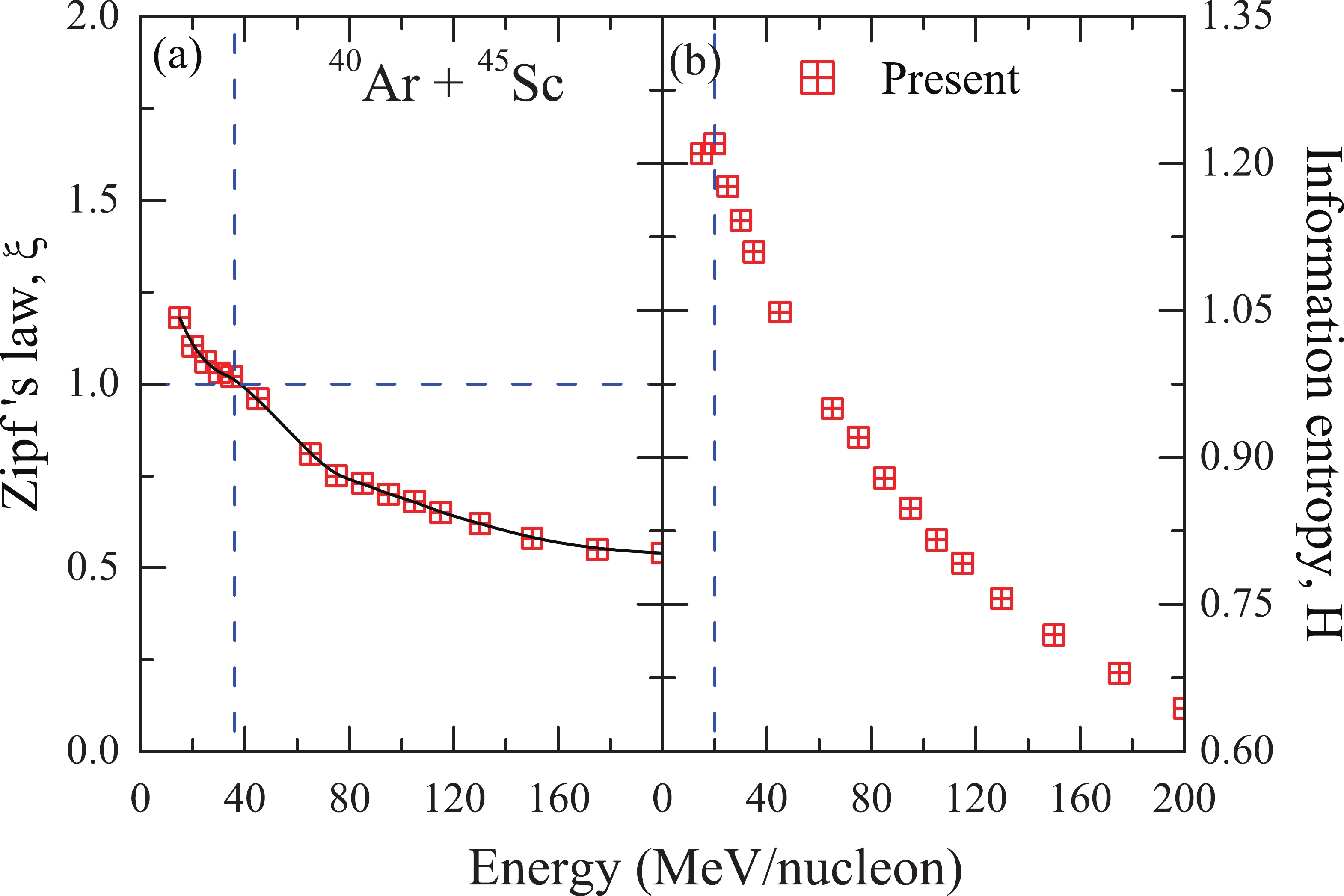
Figure 5. (color online) (a) Energy dependence of the
$ \xi $ parameter extracted from the power law fit,$ <Z_n>\propto n^{-\xi} $ ; (b) values of the information entropy (H) for 40Ar+45Sc reactions in the incident energy range of 15-200 MeV/nucleon. Zipf's law is followed when$ \xi = 1 $ , represented by the dashed horizontal line [5]. -
C. E. Shannon introduced the concept of Shannon information entropy, which measures the information contained in a message that is sent along a transmission line [53]. Since its introduction, Shannon information entropy has been applied to a wide variety of problems in fields such as nuclear/particle physics, astrophysics, life sciences, economics, and engineering (see Ref. [33] for a recent review on this). Cao and Hwa first used this concept in nuclear particle physics to study multi-particle production in high energy hadron collisions [54]. They defined the information entropy method in the whole reaction system and in event space. Y. G. Ma introduced this concept as a characteristic signal to study the liquid-gas phase transition in heavy-ion collisions. The information entropy was constructed as
$ H = - \displaystyle\sum\limits_i p_i\; ln (p_i), $

(17) with
$ \displaystyle\sum_i p_i $ = 1. Here,$ p_i $ is the normalized probability distribution of the total multiplicities having 'i' particles produced in an event. It should be kept in mind that the emphasis is on event space and not on phase space. The information entropy exhibits a peak at the point of maximum fluctuations. The results for the QMD+SACA model are shown in Fig. 5 (b). The information entropy (H) has a peak at 20 MeV/nucleon, indicating that the greatest uncertainty in the probabilities occurs at this energy. We also see that the energy at which the largest value of H occurs is consistent with our observations of other critical parameters (except Zipf's law).Combining all the results from Figs. 1-5 (except Zipf's law), our study predicts the critical point (or onset of fragmentation) for 40Ar+45Sc to be in the band of 20-23.1 MeV/nucleon, which is in close agreement with the experimentally observed value of 23.9 MeV/nucleon.
-
We next extended our study to the heavily charged system of 84Kr+197Au for the reduced impact parameter
$ \hat{b}\leqslant $ 0.25, for which no minimum in the power exponent has been observed experimentally [3]. In Fig. 6, we display the charge distributions (crossed squares) [3≤$ Z_{f} $ ≤12] obtained in the highly charged reaction of 84Kr+197Au at six different incident energies in the range of 35 to 400 MeV/nucleon. The available experimental data [3] for the same reaction are also displayed (see the stars). Note that the QMD+SACA model is able to reproduce the experimental measurements for IMFs in most of the cases.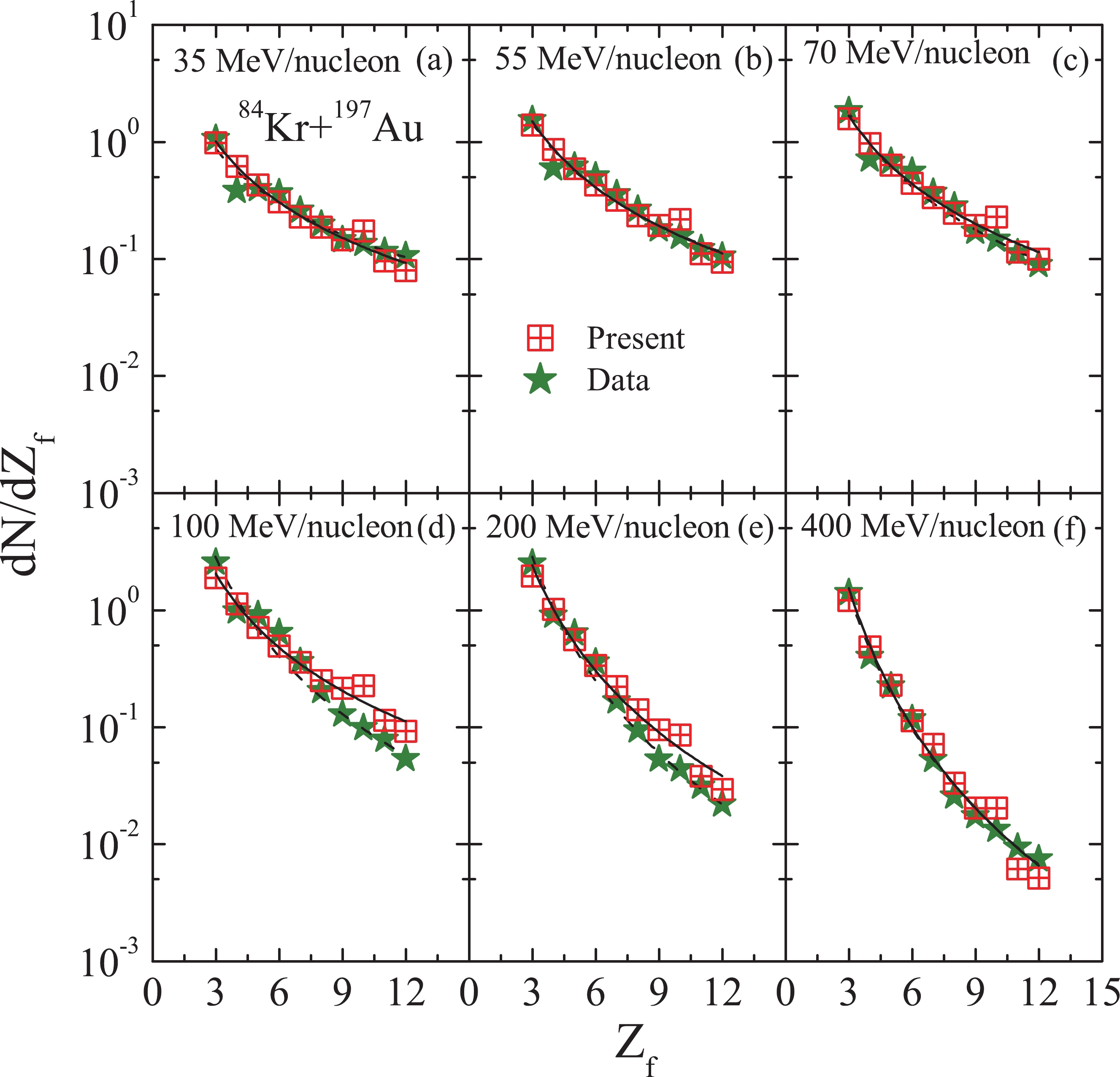
Figure 6. (color online) The charge distributions obtained from the central reactions of 84Kr+197Au at six different beam energies between 35 and 400 MeV/nucleon. The solid lines represent the power law fitting of IMFs [3≤
$ Z_f $ ≤12] obtained using the QMD + SACA model.Further, we again fit the charge yields at each incident energy with power law fits
$ \propto $ $ Z_f^{-\tau} $ , and the extracted values of the power law factor τ are plotted against the incident energy in Fig. 7. We observe that the extracted values of τ increase monotonically with the incident energy without passing through a minimum value. This absence of a minimum for τ has been attributed to the dominance of long range Coulomb forces in highly charged systems [3, 11, 26]. In the figure, we also display the results of previous calculations (represented by different lines) that used the Statistical Multifragmentation Model (SMM) with and without sequential decay [3]. In the present study, we find that the calculations using QMD+SACA give τ values that are close to the experimentally measured ones as well as to the SMM calculations with sequential decay [3]. In the inset, we also display the results of τ down to the incident energy of 15 MeV/nucleon: no minimum is seen in the extracted values of τ. We also analyzed the other critical parameters$ \lambda $ ,$ <S_{2}> $ ,$ <\gamma_{2}> $ ,$ <Z_{\rm max2}> $ , P,$ S_p $ , H, and Zipf's law for this highly charged system (results are not shown here) and observed no characteristic signal of the liquid-gas phase transition. The absence of liquid-gas phase-transition signals is due to the Coulomb forces in this highly charged system.
Figure 7. (color online) Extracted values of the power law factor τ, obtained from the power law fits of IMFs [3≤
$ Z_{f} $ ≤12] for the central reactions of 84Kr+197Au as shown in Fig. 6. The symbols have the same meaning as in Fig. 1. Here, different lines represent the Statistical Multifragmentation Model (SMM) calculations with and without sequential decay [3].The consistency of the QMD+SACA approach in reproducing experimental data for light and heavily charged systems gives us confidence that it can provide reliable information about the critical point of the liquid-gas phase transition or the point of onset of multifragmentation. It is worth mentioning that the SACA method does not have free parameters as in other calculations. Moreover, the fragments can be realized as early as
$ \sim $ 60-90 fm/c, when the nuclear matter is still hot and dense. Moreover, the QMD+SACA model provides results that are consistent between all of the characteristic signals of the liquid-gas phase-transition, except for Zipf's law, for which the model gives a higher critical energy value for the lighter system. The present study therefore suggests that Zipf's law is not suitable for predicting the liquid-gas phase transition [20, 39]. Further, this study provides the first consistent calculation that is in accordance with the onset of fragmentation in the lighter system and the subsequent absence of such trends in the highly charged system. Recently, Lin et al. [20] used the SMM and studied various critical signals for primary and secondary fragments. It was found that few signals may give different results for primary and secondary fragments. In the present results, in which SACA gives realistic fragments, all signals except Zipf's law yield characteristic signals for the lighter system. Therefore, no additional statistical decay codes are required. Considering the consistency of the QMD+SACA model, it can be used to guide the experiments to study possible liquid-gas phase transitions in nuclear matter. -
In this article, we investigated the charge yield of fragments and its connection with the liquid-gas phase transition (i.e., the onset of multifragmentation) in light and heavily charged systems of 40Ar+45Sc and 84Kr+197Au, respectively. We also used various parameters and found that the QMD+SACA calculations are consistent with the experimental measurements. Using different critical parameters, we obtained a critical point of the liquid-gas phase transition or the point of onset of multifragmentation between 20-23.1 MeV/nucleon for the 40Ar+45Sc system (Zipf's law was an exception, predicting a critical energy of
$ \sim $ 35 MeV/nucleon), which is close to the experimentally observed value of 23.9 MeV/nucleon. No such critical point of the liquid-gas phase transition (or onset of multifragmentation) was observed for 84Kr+197Au, in agreement with experimental findings and other theoretical calculations. We feel that the existing model is highly suggestive of the critical behavior in lighter colliding systems, although more work needs to be performed to establish this more firmly. We believe that the present model is one step ahead of the QMD model coupled with the MST algorithm or its variants, and that it is also helpful for the analysis of experimental data for light and heavily charged systems. We believe that the QMD+SACA model can be useful in guiding future experiments.
Fragment emission and critical behavior in light and heavy charged systems
- Received Date: 2020-06-03
- Available Online: 2021-01-15
Abstract: We study the emission of fragments in central collisions of light and heavily charged systems of 40Ar+45Sc and 84Kr+197Au, respectively, using the Quantum Molecular Dynamics (QMD) model as the primary model. The fragments are identified using an energy based clusterization algorithm, i.e., the Simulated Annealing Clusterization Algorithm (SACA). The charge distributions of intermediate mass fragments [3≤





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF





















 DownLoad:
DownLoad: