-
Einstein’s theory of general relativity (GR) was proposed over a century ago and has successfully passed a large number of observational tests, primarily in the weak field regime. One of the most impressive results derived from GR is the prediction of black holes. Their existence as physical objects is consistent with available observations of gravitational waves generated by the merging of black holes according to the LIGO experiment [1, 2], through the extraordinary observation of the M87* black hole shadow by the Event Horizon Collaboration [3], and also with observation of the electromagnetic spectrum emitted from an accretion disk around a black hole [4-6]. With these observations of black holes in the gravitational and electromagnetic spectra, together with their future developments, tests of GR and its alternatives in the strong gravity regime are currently gaining considerable attention.
In the strong gravity regime, the observational aspects of black holes are closely related to a narrow region not far from the event horizon, ranging from the photon sphere to the accretion disk around the black hole. This region is naturally of great significance, as it is perhaps influenced by the possible higher curvature corrections to the Einstein term in GR. The Gauss-Bonnet term and its Lovelock generalization are the most important higher curvature terms studied in various alternative theories beyond GR. However, in four dimensions, the Gauss-Bonnet term is a topological invariant and thus does not contribute to the gravitational dynamics; instead, it is coupled to a matter field. Recently, a novel 4EGB theory of gravity was proposed by Glavan and Lin [7], which includes a regularized Gauss-Bonnet term using the re-scaling of the Gauss-Bonnet coupling constant
$ \alpha \to \alpha/(D-4) $ in the limit$ D\to 4 $ . With such scaling, the Gauss-Bonnet term can make a non-trivial contribution to the gravitational dynamics in the limit$ D \to 4 $ . However, this modification is in contradiction with common knowledge and might cause some problems. This theory is not well defined in the limit$ D \rightarrow 4 $ [8-14]. Furthermore, the vacua of the model are also ill-defined [15]. To solve these issues, several variants of the original theory have been explored. In [10], it is shown that the original 4EGB theory can be reformulated to a specific class of the Horndeski theory with an additional scalar degree of freedom. Its Lovelock generalization as a scalar-tensor theory has also been considered in [11]. Similar results have also been explored in [12, 13] by adding a counter term in D-dimensions and then taking the$ D\to 4 $ limit. Another regularization procedure is to break the temporal diffeomorphism invariance of the theory [16]. In this way, the scalar degree of freedom can be eliminated by a Lagrangian multiplier so that the theory has the same number of degrees of freedom as GR.Both the original 4EGB theory and its variants have attracted much attention recently. The black hole solutions [17, 18] and their physical properties, such as shadows [19-21], quasi-normal modes [19, 22], the stability of gravitational perturbations [23], the innermost circular orbits of massive and spinning particles [24, 25], rotating black holes [26], charged black holes in anti-de Sitter (AdS) space [27], radiating black holes [28, 29], relativistic star solutions [30], the gray-body factor and Hawking radiation [31, 32], the stability of the Einstein static universe [33], gravitational lensing [34, 35], the effect of the speed of gravitational waves and scalar perturbations [36], observational constraints on the 4EGB theoretical parameter
$ \alpha $ [36, 37], and thermodynamic geometry and phase transitions [38-41], have been extensively analyzed. The BTZ black hole in three-dimensional Einstein-Lovelock gravity has also been explored [42]. It is worth noting that the holographic implications of the addition of the Gauss-Bonnet term to the AdS gravity action in four dimensions is addressed in [43].In this paper, we explore the properties of the electromagnetic spectrum emitted from the accretion disk around a static spherically symmetric black hole in 4EGB gravity. For an astrophysical black hole, the study of the electromagnetic spectrum from the accretion process around the black hole is a powerful approach to explore the nature of the black hole spacetime in the strong gravity regime. This has stimulated many studies of the thin accretion disk around various black hole spacetimes; see [44-74] and the references therein. Therefore, it is natural to ask whether the Gauss-Bonnet corrections of 4EGB gravity can appear in the electromagnetic signatures of the accretion disk. To answer this question, we consider a thin relativistic accretion disk model around a 4EGB black hole, which is in a steady-state and in hydrodynamic and thermodynamic equilibrium. In particular, we calculate the energy flux, temperature distribution, and electromagnetic spectrum of the thin accretion disk and compare these values with those in the standard GR case. The possible effects of the Gauss-Bonnet corrections on the electromagnetic signatures from the thin accretion disk are also explored.
The organization of our paper is as follows. In Sec. II, we present a brief introduction of the recently proposed 4EGB gravity and its static spherically symmetric black hole solution. In Sec. III, we study the geodesic equations for the timelike particles moving in the equatorial plane in the 4EGB black hole. Then, in Sec. IV, we study the physical properties of the electromagnetic spectrum emitted from the thin accretion disk around a 4EGB black hole and explore the effects of the Gauss-Bonnet coupling constant
$ \alpha $ on the energy flux, temperature distribution, electromagnetic spectrum, and accretion efficiency of the accretion disk. A summary and discussion are presented in Sec. V. -
In this section, we discuss the theoretical background relevant to analysis of the thin accretion disk around a 4EGB black hole.
Let us start with the original action of the D-dimensional Einstein-Gauss-Bonnet gravity, which is
$ S_{\rm EGB} = \int {\rm d}^D x \sqrt{-g} \left(\frac{M_{\rm Pl}^2}{2} R + \alpha R_{\rm GB}^2\right), $

(1) where R is the Ricci scalar of spacetime,
$ R^2_{\rm{GB}} \equiv R_{\mu\nu\rho\sigma}R^{\mu\nu\rho\sigma}-4 R_{\mu\nu}R^{\mu\nu}+R^2 $ is the Gauss-Bonnet term, and$ \alpha $ is the dimensionless coupling constant. Here,$ M_{\rm Pl} = (8\pi G)^{-1/2} $ is the reduced Planck energy, with G being the gravitational constant. In four dimensional spacetime, the Gauss-Bonnet term$ R^2_{\rm{GB}} $ is a total derivative; therefore, it does not contribute to the gravitational dynamics. However, by re-scaling the coupling constant as$ \alpha \to \alpha/(D-4) $ , it is shown by Glaan and Lin [7] that the Gauss-Bonnet invariant can make a non-trivial contribution to the gravitational dynamics in the limit$ D \to 4 $ . With such scaling, the action of the 4EGB in the limit$ D\to 4 $ can be written as [7]$ S_{\rm 4EGB} = \int {\rm d}^D x \sqrt{-g} \left(\frac{M_{\rm Pl}^2}{2} R + \frac{\alpha}{D-4} R_{\rm GB}^2\right). $

(2) Variation of this action with respect to the metric leads to the field equation of 4EGB in a vacuum,
$ R_{\mu \nu} - \frac{1}{2} R g_{\mu\nu} + \frac{\alpha M_{\rm Pl}^{-2}}{D-4} H_{\mu\nu} = 0, $

(3) where
$ \begin{aligned}[b] H_{\mu\nu} =& 2 (RR_{\mu\nu} - 2 R_{\mu \gamma} R^{\gamma}_\nu - 2 R^{\lambda \rho} R_{\mu \lambda \nu \rho} + R_{\mu}^{\lambda \rho \sigma} R_{\nu \lambda \rho \sigma}) \\ & - \frac{1}{2} g_{\mu\nu} R^2_{\rm{GB}}. \end{aligned} $

(4) Here, we would like to mention that
$ H_{\mu \nu} $ is proportional to$ D-4 $ in D-dimensional spacetime; therefore, in the field equation (3), the Gauss-Bonnet contribution$ \alpha H_{\mu \nu}/(D-4) $ can be non-vanishing, even in the limit$ D\to 4 $ .However, as mentioned in the previous section, the theory defined in this way has no well-defined limit [8-14]. There are several schemes to overcome this difficulty in literature. One approach is to reformulate the original version to a specific class of the Horendeski theory, which has the following action [10-13],
$ \begin{aligned}[b] S = & \int_{{\cal M}}{\rm d}^4 x\sqrt{-g}\bigg[ \frac{M_{\rm Pl}^2}{2}R- 2\Lambda_0 + \hat{\alpha}\big(4G^{\mu\nu}\nabla_\mu \phi\nabla_\nu \phi \\ & - \phi R_{\rm GB}^2+4\square\phi(\nabla \phi)^2+2 (\nabla\phi)^4 \big) \bigg]+S_m, \end{aligned}$

(5) where
$ \phi $ is a scalar field inherent from D dimensions. In [12, 13], it is introduced by a conformal transformation$ g_{ab}\rightarrow {\rm e}^{2\phi}g_{ab} $ . In [10, 11], it is introduced by Kaluza-Klein reduction of the metric${\rm d}s^2_D = {\rm d}s^2_4+{\rm e}^{2\phi}{\rm d}\Omega^2_{D-4}$ .Another approach is based on the ADM decomposition analysis and breaks the temporal diffeomorphism invaiance of the theory [16]. In this way, the theory only has spatial covariance, and one can write the 4-dimensional spacetime metric as
$ \begin{aligned} {\rm d}s^2 & = g_{\mu\nu} {\rm d}x^\mu {\rm d} x^\nu \\ & = -N^2 {\rm d}t^2+\gamma_{ij}({\rm d}x^i+N^i {\rm d}t)({\rm d}x^j+N^j {\rm d}t),\end{aligned} $

(6) where N,
$ N^i $ , and$ \gamma_{ij} $ are the lapse function, shift vector, and spatial metric, respectively. The action of the spatial covariant 4EGB theory can be constructed as [16]$ \begin{aligned}[b] S_{\rm{EGB}}& = \int {\rm d}t {\rm d}^3 x \sqrt{\gamma} N \Bigg\{\frac{M_{\rm Pl}^2}{2} (\;^3R-2 \Lambda+{\cal K}_{ij} {\cal K}^{ij} - {\cal K}^2) \\ & +\alpha \Big[ -\frac{4}{3} (8 \;^3R_{ij} \;^3R^{ij}-4 \;^3R_{ij} {\cal M}^{ij} - {\cal M}_{ij} {\cal M}^{ij}) \\ & +\frac{1}{2}(8 \;^3 R^2 -4 \;^3 R {\cal M} - {\cal M}^2)\Big]\Bigg\},\end{aligned}$

(7) where
$ {\cal K}_{ij} = \frac{1}{2N} (\partial_t \gamma_{ij} -2 D_{(i}N_{j)} - \gamma_{ij} D^2 \lambda_{\rm GF}), $

(8) $ {\cal K} = \gamma^{ij} {\cal K}_{ij}, $

(9) $ {\cal M}_{ij} =^3 R_{ij}+ {\cal K} {\cal K}_{ij} - {\cal K}_{ik} {\cal K}^k_j, $

(10) $ {\cal M} = \gamma^{ij} {\cal M}_{ij}, $

(11) with D denoting the spatial covariant derivative and
$ \lambda_{\rm GF} $ being the Lagrangian multiplier.In all of the theories mentioned above, for either the original version or its variants, the static, spherically symmetric black hole solution shares the same metric form,
$ {\rm d}s^2 = - f(r) {\rm d}t^2 + \frac{{\rm d}r^2}{f(r)} + r^2 \bar \gamma_{ij} {\rm d}x^{i} {\rm d}x^j, $

(12) $ f(r) = 1+ \frac{r^2 }{16\pi G \alpha} \left(1 \pm \sqrt{1 + \frac{64 \pi \alpha G^2 M}{r^3}}\right), $

(13) where
$ \bar \gamma_{ij} $ is the metric of an$ n\equiv D-2 $ dimensional unit sphere. In the$ D\to 4 $ limit,$ n \to 2 $ . M denotes the mass of the black hole, and the Gauss-Bonnet coupling constant$ \alpha $ is restricted to$ -8 G M^2 \leqslant 8\pi \alpha \leqslant G M^2 $ [24]. The horizon of the black hole is given by$ r_{\pm} = GM\left(1 \pm \sqrt{1- \frac{8\pi \alpha }{G M^2}}\right), $

(14) where there are two horizons when
$ \alpha>0 $ and one degenerate horizon when$ 8 \pi \alpha = G M^2 $ . When$ \alpha $ is negative, the spacetime is also well defined beyond the horizon if$ -8G M^2 \leqslant 8 \pi \alpha \leqslant 0 $ . In this case, the black hole only has one horizon, which is given by$ r_+ = GM \left(1 + \sqrt{1 - \frac{8\pi \alpha}{G M^2} } \right). $

(15) In this paper, we consider the black hole solution in the region
$ -8 G M^2 \leqslant 8 \pi \alpha \leqslant G M^2 $ . It is worth noting that the above solution was also found in gravity with a conformal anomaly in [75] and was extended to the case with a cosmological constant in [76]. -
The accretion disk is formed by particles moving in a circular orbit around a compact object, the physical properties and electromagnetic radiation characteristics of which are determined by the space-time geometry around the compact object. To study the electromagnetic properties of the thin accretion disk around a 4EGB black hole, let us first consider the evolution of a massive particle in the black hole spacetime. We start with the Lagrangian of the particle,
$ L = \frac{1}{2}g_{\mu \nu} \frac{{\rm d} x^\mu} {{\rm d} \lambda } \frac{{\rm d} x^\nu}{{\rm d} \lambda}, $

(16) where
$ \lambda $ denotes the affine parameter of the world line of the particle. For a massless particle, we have$ L = 0 $ , and for a massive one,$ L <0 $ . Then, the generalized momentum$ p_\mu $ of the particle can be obtained as$ p_{\mu} = \frac{\partial L}{\partial \dot x^{\mu}} = g_{\mu\nu} \dot x^\nu, $

(17) which leads to four equations of motions for a particle with energy E and angular momentum l,
$ p_t = g_{tt} \dot t = - \tilde{E}, $

(18) $ p_\phi = g_{\phi \phi} \dot \phi = \tilde{l},$

(19) $ p_r = g_{rr} \dot r, $

(20) $ p_\theta = g_{\theta \theta} \dot \theta. $

(21) Here, a dot denotes the derivative with respect to the affine parameter
$ \lambda $ of the geodesics. From these expressions, we obtain$ \dot t = - \frac{ \tilde{E} }{ g_{tt} } = \frac{\tilde{E}}{f(r)}, $

(22) $ \dot \phi = \frac{ \tilde{l}}{g_{\phi\phi}} = \frac{\tilde{l}}{r^2 \sin^2\theta}. $

(23) For timelike geodesics, we have
$ g_{\mu \nu} \dot x^\mu \dot x^\nu = -1 $ . Substituting$ \dot t $ and$ \dot \phi $ , we get$ g_{rr} \dot r^2 + g_{\theta \theta} \dot \theta^2 = -1 - g_{tt} \dot t^2 - g_{\phi\phi} \dot \phi^2 \\ = -1 +\frac{\tilde{E}^2}{f(r)}- \frac{\tilde{l}^2}{r^2\sin^2\theta}. $

(24) We are interested in the evolution of the particle in the equatorial circular orbit. For this reason, we can consider
$ \theta = \pi/2 $ and$ \dot \theta = 0 $ for simplicity. Then, the above expression can be simplified into the form$ \dot r ^2 = \tilde{E}^2 - V_{\rm eff}(r), $

(25) where
$ V_{\rm eff}(r) $ denotes the effective potential and is given by$ V_{\rm eff}(r) = \left(1+\frac{\tilde{l}^2}{r^2}\right)f(r). $

(26) It is immediately clear that
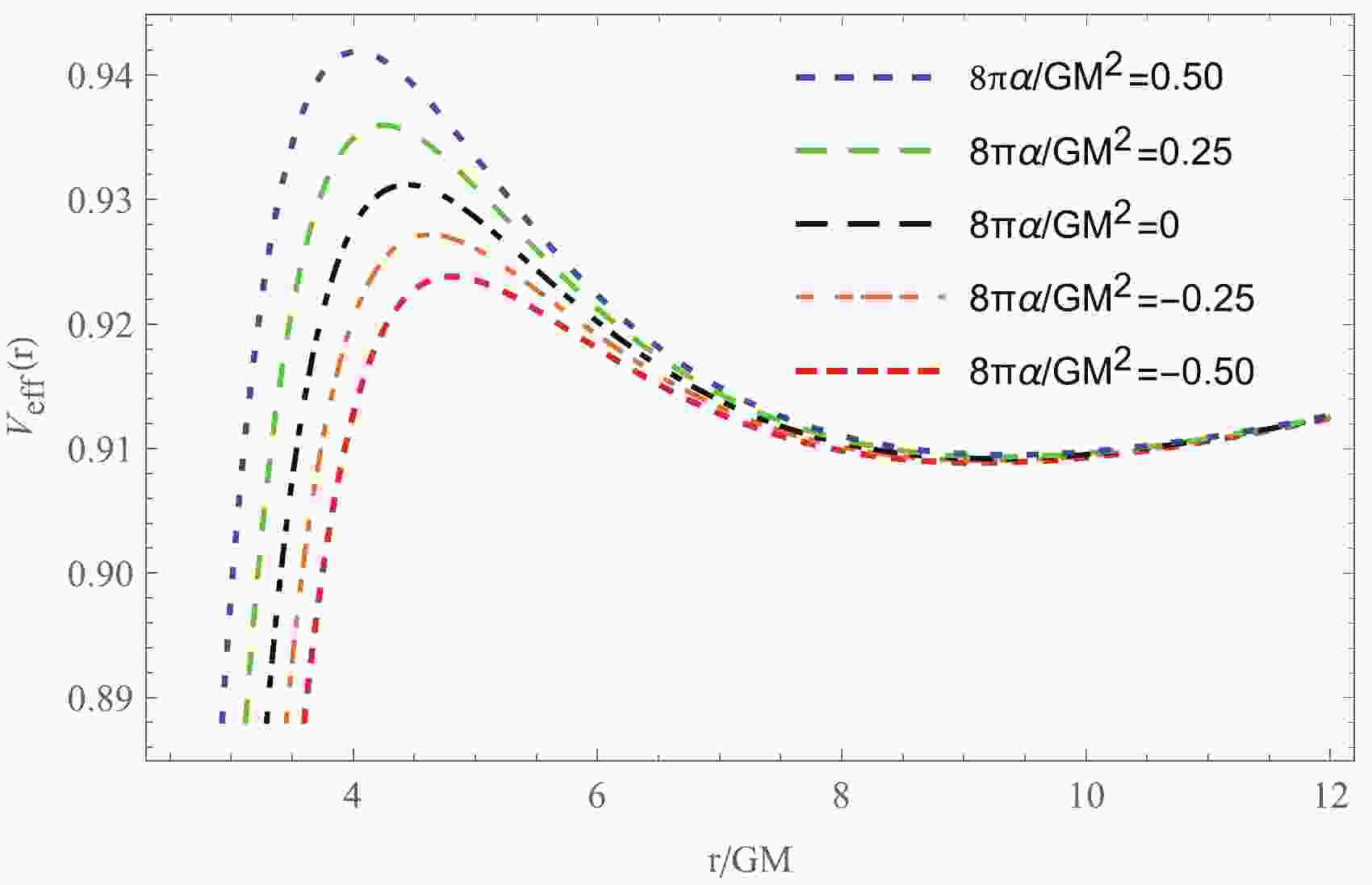
$ V_{\rm eff}(r) \to 1 $ as$ r \to +\infty $ , as expected for an asymptotically flat spacetime. In this case, particles with energy$ \tilde{E} >1 $ can escape to infinity, and$ \tilde{E} = 1 $ is the critical case between bound and unbound orbits. In this sense, the maximum energy for the bound orbits is$ \tilde{E} = 1 $ . Fig. 1 clearly shows how the effective potential of a particle in the 4EGB black hole spacetime depends on the Gauss-Bonnet coupling constant$ \alpha $ . In this figure, the peak of the effective potential of a particle increases with$ \alpha $ . The stable circular orbits in the equatorial plane correspond to those orbits with constant r, i.e.,$ \dot r^2 = 0 $ and${\rm d}V_{\rm eff}(r)/{\rm d}r = 0$ . Under these conditions, the specific energy$ \tilde{E} $ , the specific angular momentum$ \tilde{l} $ , and the angular velocity$ \Omega $ of a particle moving in a circular orbit in the 4EGB black hole can be written as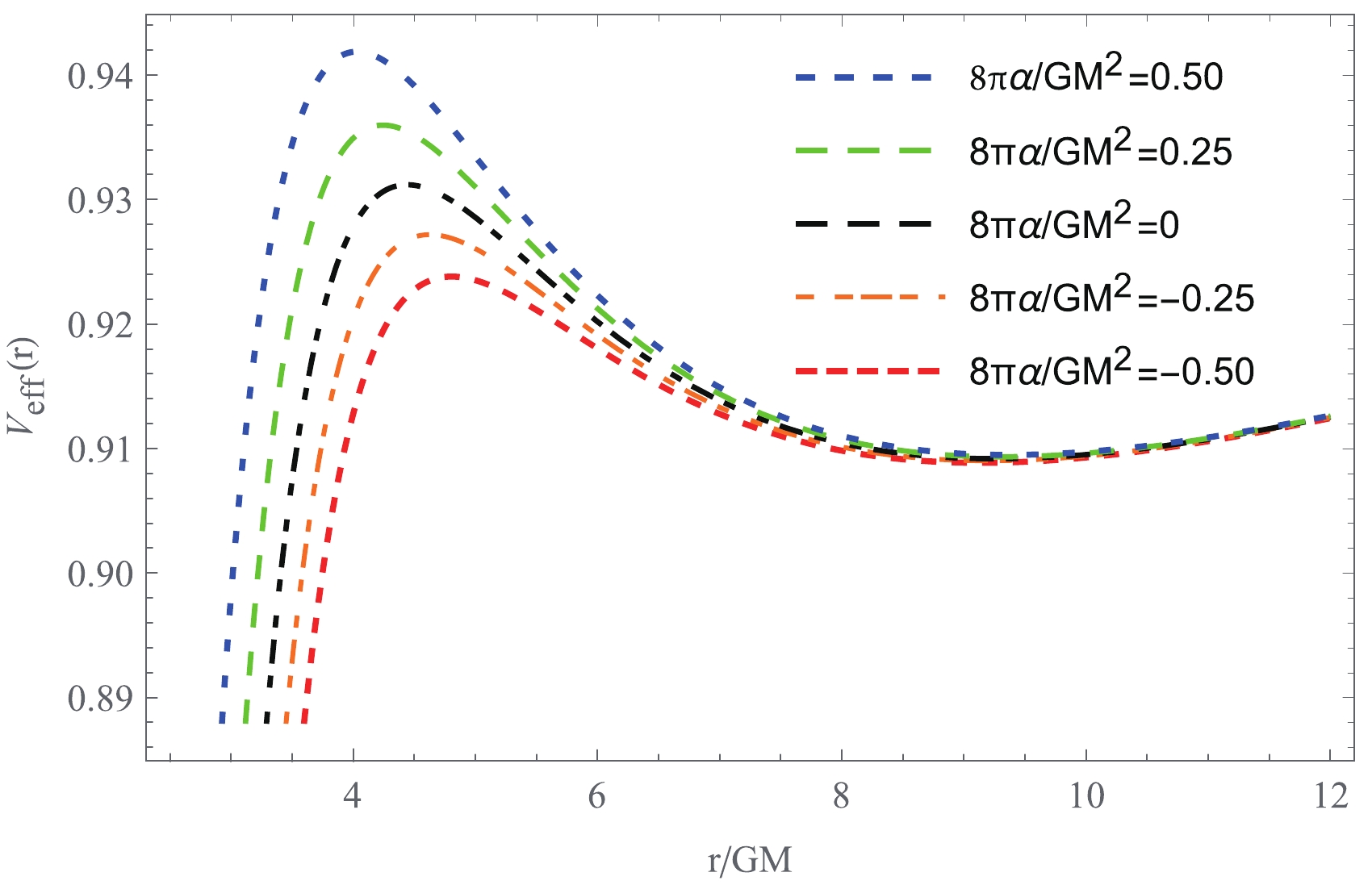
Figure 1. (color online) Effective potential of a particle with
$\tilde{l}= 3.7$ in the 4EGB black hole spacetime.$ \tilde{E} = -\frac{g_{tt}}{\sqrt{-g_{tt}-g_{\phi\phi}\Omega^2}} = \frac{f(r)}{\sqrt{f(r)-\frac{1}{2} r f'(r)}} , $

(27) $ \tilde{l} = \frac{g_{\phi\phi}\Omega}{\sqrt{-g_{tt}-g_{\phi\phi}\Omega^2}} = \frac{r \sqrt{r f'(r)}}{\sqrt{2 f(r)-r f'(r)}} , $

(28) $ \Omega = \frac{{\rm d}\phi}{{\rm d}t} = \frac{f'(r)}{ \sqrt{2r f'(r)}}. $

(29) The marginally stable circular orbits around the 4EGB black hole can be determined from the condition
$ {\rm d}^2V_{\rm eff}(r)/{\rm d}r^2 = 0. $

(30) Combining this equation with (27) and (28) and solving for r, the radius of the marginally stable circular orbit can be calculated as
$ r_{\rm ms} = \frac{3 f(r_{\rm ms})f'(r_{\rm ms})}{2f'^2(r_{\rm ms}) - f(r_{\rm ms}) f''(r_{\rm ms})}, $

(31) which does not admit any analytic solution. We solve it numerically and plot the result in Fig. 2, which clearly shows that the radius of the marginally stable circular orbit
$ r_{\rm ms} $ decreases with increasing Gauss-Bonnet coupling constant$ \alpha $ . In addition, we give an approximate analytic result for the marginally stable circular orbits using a Taylor expansion when$ \alpha $ is small, which yields
Figure 2. (color online) Marginally stable orbit radius
$r_{\rm ms}$ as a function of the Gauss-Bonnet coupling constant$\alpha$ for particles moving in the thin accretion disk around the 4EGB black hole.$ r_{\rm{ms}} = 6 GM - \frac{44 \pi }{9M}\alpha + O(\alpha^2). $

(32) This approximate analytic result clearly shows that positive values for
$ \alpha $ tend to decrease the radius of the marginally stable circular orbits. Here, we would like to mention that the evolution of the massive particles in the 4EGB black hole and the marginally stable circular orbits have also been studied in [24]. -
In this section, we consider the steady-state thin accretion disk model and apply it to studying the accretion process around the 4EGB black hole. For this purpose, we adopt the Novikov-Thorne model of a thin accretion disk consisting of anisotropic fluid moving in the equatorial plane [77, 78]. In this model, the disk height H is negligible compared with the characteristic radius R of the disk, i.e.,
$ H \ll R $ . This assumption leads to the metric components$ g_ {tt} $ ,$ g_ {t\phi } $ ,$ g_ {rr} $ ,$ g_ {\theta \theta} $ , and$ g_ {\phi \phi} $ only depending on the radial coordinate r. The disk is also assumed to be stabilized at hydrodynamic equilibrium, with the pressure and vertical entropy gradient being negligible. An efficient cooling mechanism via heat loss by radiation over the disk surface is assumed to be functioning in the disk, which prevents the disk from collecting the heat generated by stresses and dynamic friction. The thin accretion disk has an inner edge at the marginally stable orbit of the compact object potential, and the accreting matter has a Keplerian motion in higher orbits.The physical properties of the accretion disk are governed by certain structure equations, which arise from the requirement of the conservation of the rest mass, the energy, and the angular momentum of the fluid. In the thin accretion disk model, the stress-energy tensor of the accreting matter in the disk can be decomposed according to [77, 78]
$ T^{\mu\nu} = \rho_0 u^\mu u^\nu +2 u^{(\mu}q^{\nu)}+t^{\mu\nu}, $

(33) where
$ u_\mu q^\mu = 0, \; \; \; u_\mu t^{\mu\nu} = 0, $

(34) where the quantities
$ \rho_0 $ ,$ q^\mu $ , and$ t^{\mu\nu} $ represent the rest mass density, the energy flow vector, and the stress tensor of the accreting matter, respectively, as defined in the averaged rest-frame of the orbiting particle with four-velocity$ u^\mu $ . From the equation, if the rest mass is conserved, i.e.,$ \nabla_\mu (\rho_0 u^\mu) = 0 $ , it follows that the time averaged rate of accretion of the rest mass is independent of the disk radius,$ \dot{M}_0 = -2\pi \sqrt{-g} \Sigma u^r = {\rm const.}, $

(35) $ \Sigma (r) = \int^H_{-H}<\rho_0>{\rm d}z, $

(36) where
$ \Sigma(r) $ is the time-averaged surface density, and z denotes cylindrical coordinates. According to the conservation law of the energy and the law of the angular momentum conservation$ \nabla_\mu T^{t \mu} = 0, \; \; \; \nabla_\mu T^{\phi \mu} = 0, $

(37) one can obtain the time-averaged radial structure equations of the thin disk around the 4EGB black hole,
$ [\dot{M}_0\tilde{E}-2\pi \sqrt{-g} \Omega W^r_\phi]_{,r} = 4 \pi r F(r)\tilde{E}, $

(38) $ [\dot{M}_0\tilde{l}-2\pi \sqrt{-g} W^r_\phi]_{,r} = 4 \pi r F(r) \tilde{l}, $

(39) where
$ W^r_\phi $ is the averaged torque and is given by$ W^r_\phi = \int^H_{-H}<t^r_\phi>{\rm d}z, \; \; \; \sqrt{-{\cal G}} = \sqrt{1+l}r. $

(40) The quantity
$ <t^r_\phi> $ is the average value of the$ \phi $ -r component of the stress tensor over a characteristic time scale$ \Delta t $ at the azimuthal angle$ \Delta \phi = 2 \pi $ . By applying the energy-angular momentum relation$ \tilde{E}_{,r} = \omega \tilde{l}_{,r} $ , the flux$ F(r) $ of the radiant energy over the disk can be expressed in terms of the specific energy, angular momentum, and angular velocity of the orbiting particle in the thin accretion disk around the 4EGB black hole,$ F(r) = -\frac{\dot{M}_0}{4\pi \sqrt{-g}}\frac{\Omega_{,r}}{(\tilde{E}-\Omega\tilde{l})^2} \int^r_{r_{\rm ms}}(\tilde{E} -\Omega \tilde{l})\tilde{l}_{,r} {\rm d}r, $

(41) where
$ r_{\rm ms} $ is the inner edge of the thin accretion disk and is assumed to be at the radius of the marginally stable circular orbit around the 4EGB black hole.We calculate the radiation flux
$ F(r) $ numerically and illustrate its behavior as a function of the radial distance for various values of the Gauss-Bonnet coupling constant$ \alpha $ . Following [46, 47], here, we consider the mass accretion driven by the 4EGB black hole with a total mass$ M = 10^6 M_{\odot} $ and a mass accretion rate of$ \dot M_0 = 10^{-12} M_{\odot} /{\rm yr} $ . In Fig. 3, we present the energy flux profile$ F(r) $ radiated by a thin accretion disk around the 4EGB black hole for various values of the Gauss-Bonnet coupling constant$ \alpha $ . The energy flux grows monotonically with increasing value of$ \alpha $ . The figure shows that the energy flux possesses a single maximum, which also grows monotonically with increasing$ \alpha $ . At the same time, its radial position is shifted toward the location of the horizon. The main reason is that for positive$ \alpha $ , the effect of the Gauss-Bonnet coupling constant$ \alpha $ decreases the radius of the marginally stable orbit, so that the lower limit of the integral in (41) becomes smaller, while for negative$ \alpha $ , the radius of the marginally stable orbit increases, so that the lower limit becomes larger.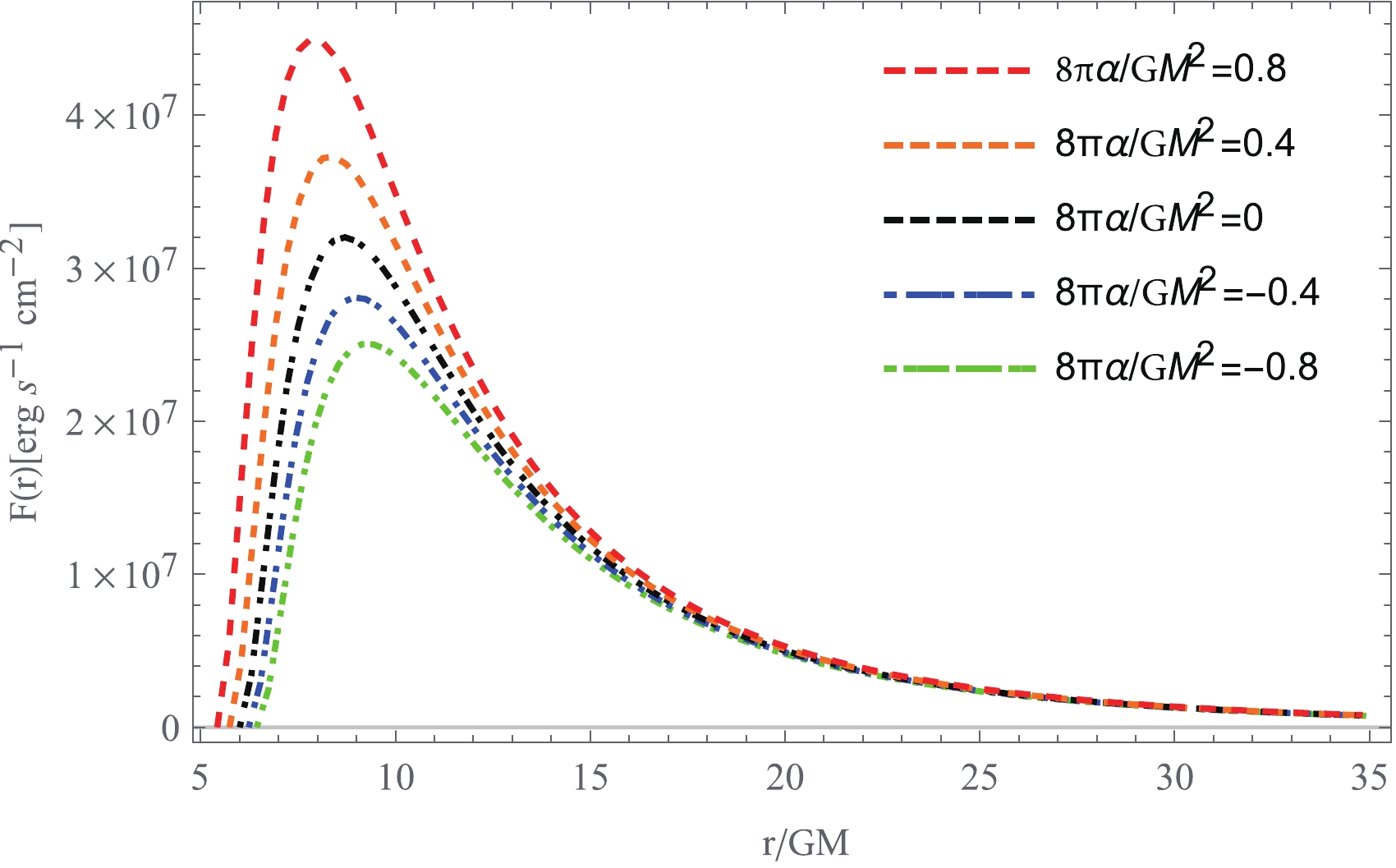
Figure 3. (color online) Dependence of the radiated energy flux over the thin accretion disk on the radial distance for various values of the Gauss-Bonnet coupling constant
$\alpha$ . Here, the mass of the black hole and the mass accretion rate are set to$10^{6} M_{\odot}$ and$10^{-12}M_{\odot}/{\rm yr}$ , respectively.The accreting matter in the steady state thin disk model is considered to be in thermodynamic equilibrium. The radiation flux
$ F(r) $ emitted by the thin accretion disk surface will thus follow the Stefan-Boltzmann law. Therefore, the effective temperature of a geometrically thin black-body disk is given by$ T_{\rm eff}(r) = \left(\frac{F(r)}{\sigma}\right)^{1/4}, $

(42) where
$ \sigma = 5.67 \times 10^{-5}\; {\rm erg}\; {\rm s}^{-1} \;{\rm cm}^{-2}\; {\rm K}^{-4} $ is the Stefan-Boltzmann constant. In Fig. 4, we display the radial profile of the effective temperature$ T_{\rm eff}(r) $ of the thin accretion disk around the 4EGB black hole for various values of the Gauss-Bonnet coupling constant$ \alpha $ . The effective temperature shows behavior similar to that of the energy flux shown in Fig. 3. It is easy to see from Fig. 4 that the temperature at the fixed radius grows monotonically with increasing value of$ \alpha $ . For a positive value of$ \alpha $ , the accretion disk is hotter than that around a Schwarzschild black hole, while it is cooler for negative$ \alpha $ .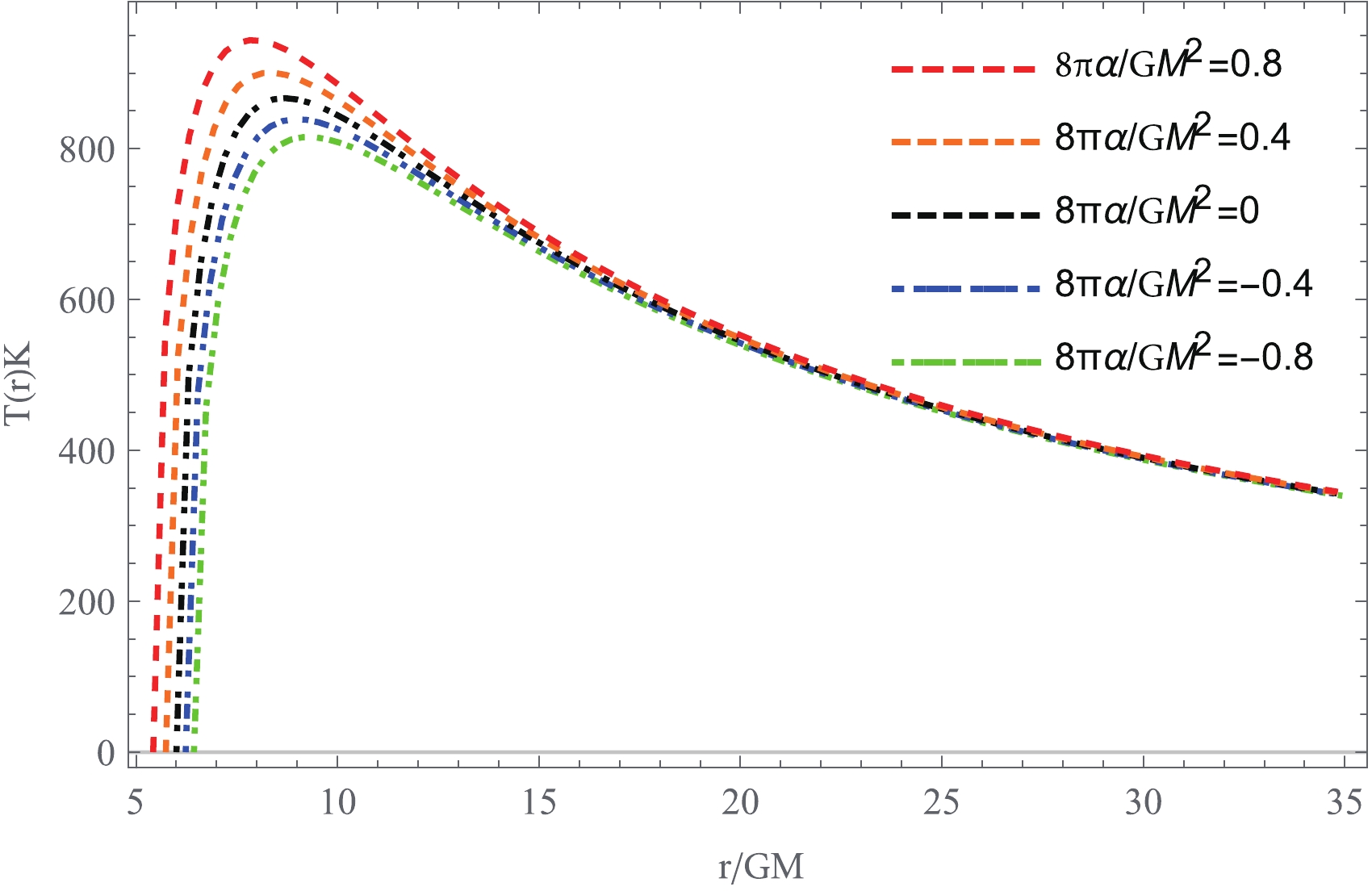
Figure 4. (color online) Temperature profile of the thin accretion disk around a static spherically symmetric black hole in the 4EGB gravity for various values of the Gauss-Bonent coupling constant
$\alpha$ . Here, the mass of the black hole and the mass accretion rate are set to$10^{6} M_{\odot}$ and$10^{-12}M_{\odot}/{\rm yr}$ , respectively.Because we consider the radiation emitted by the thin accretion disk surface as perfect black body radiation, the observed luminosity
$ L(\nu) $ of the thin accretion disk around the 4EGB black hole has a red-shifted black body spectrum [79, 80],$ \begin{aligned}[b] L(\nu) &= 4 \pi d^2 I(\nu) \\ &= \frac{8 \pi h \cos i}{c^2} \int_{r_i}^{r_f} \int_{0}^{2\pi} g^3 \frac{\nu_e^3 r {\rm d} \phi {\rm d}r}{\exp{\bigg(\dfrac{h \nu_e}{k_{\rm B} T}\bigg)}-1}, \end{aligned} $

(43) where i is the inclination angle of the thin accretion disk around the 4EGB black hole, d is the distance between the observer and the center of the thin accretion disk,
$ r_{i} $ and$ r_f $ are the inner and outer radii of the disc, respectively, h is the Planck constant,$ \nu_e $ is the emission frequency in the local rest frame of the emitter,$ I(\nu) $ is the Planck distribution,$ k_{\rm B} $ is the Boltzmann constant, and g is the redshift factor$ g = \frac{\nu}{\nu_e} = \frac{k_\mu u^\mu_o}{k_\mu u^\mu_e}, $

(44) where
$ \nu $ is the radiation fraquency in the local rest frame of the distant observer,$ u^\mu_o = (1,0,0,0) $ is the 4-velocity of the observer, and$ u^\mu_e = (u^t_e,0,0,\Omega u^t_e) $ is the 4-velocity of the emitter. Because the flux over the disk surface vanishes at$ r \to +\infty $ for asymptotically flat geometry, in this paper, we take$ r_i = r_{\rm ms} $ and$ r_f = +\infty $ . To illustrate the effect of the Gauss-Bonnet term in the emission spectrum, we calculate the radiation spectrum$ \nu L(\nu) $ numerically and display its behavior as a function of the observed frequency$ \nu $ for various values of the Gauss-Bonnet coupling constant$ \alpha $ in Fig. 5. For positive$ \alpha $ , increasing values of$ \alpha $ produce greater maximal amplitude of the disk emission spectrum as compared with the standard Schwarzschild case, while negative$ \alpha $ produces a smaller maximal amplitude. The figure also shows that the cut-off frequencies of the emission spectra increase for positive$ \alpha $ and decrease for negative$ \alpha $ , from the value corresponding to the standard Schwarzschild black hole.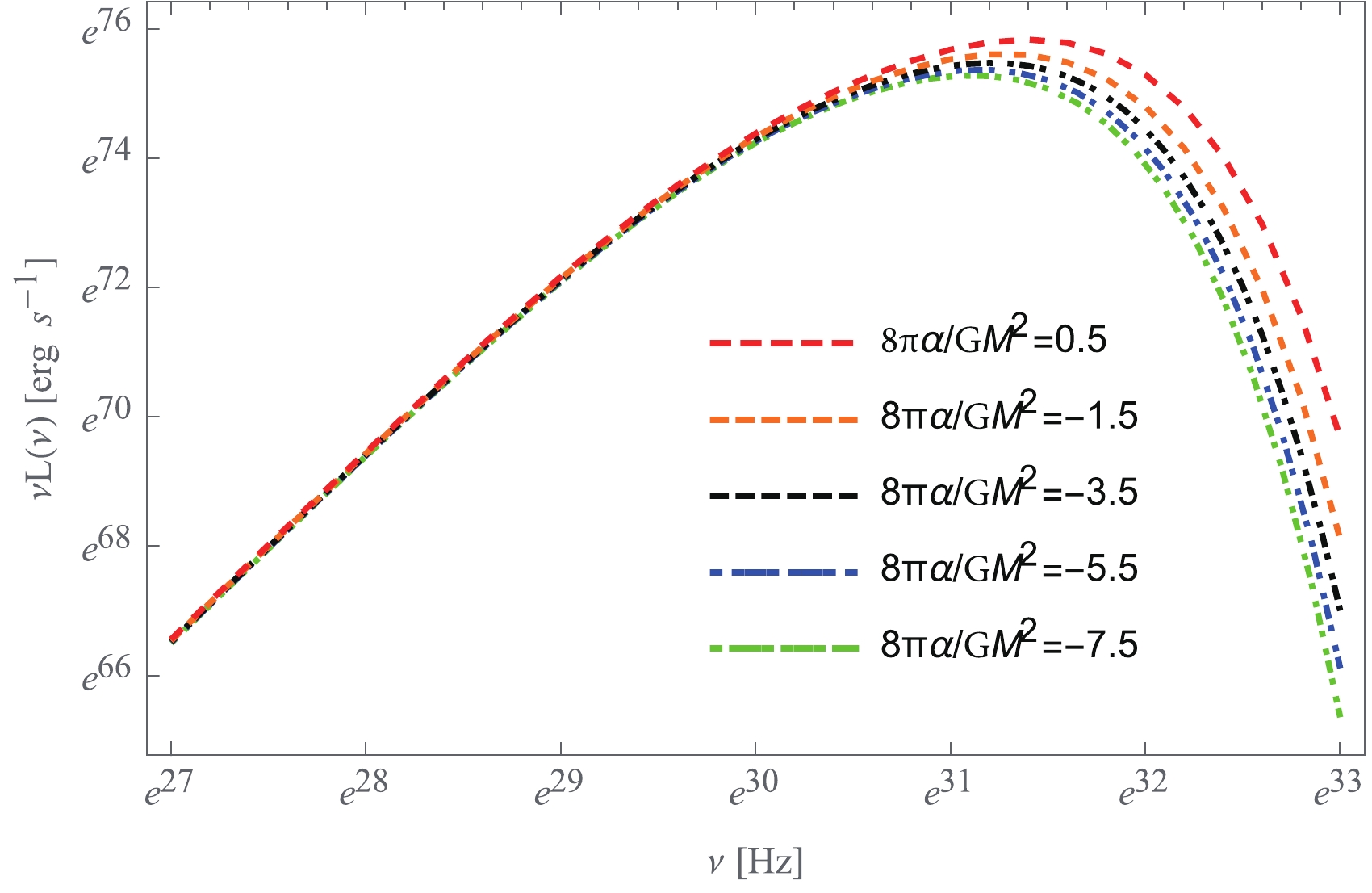
Figure 5. (color online) Emission spectrum profile for the thin accretion disk around the 4EGB black hole for various values of the Gauss-Bonnet coupling constant
$\alpha$ . Here, the mass of the black hole and the mass accretion rate are set to$10^{6} M_{\odot}$ and$10^{-12}M_{\odot}/{\rm yr}$ , respectively.Finally, let us consider the accretion efficiency of the 4EGB black hole, which is defined as the ratio between the rate of the radiation of the energy of photons escaping from the disk surface to infinity and the rate at which mass-energy is transported to the black hole [77, 78]. If all the emitted photons can escape to infinity, the efficiency
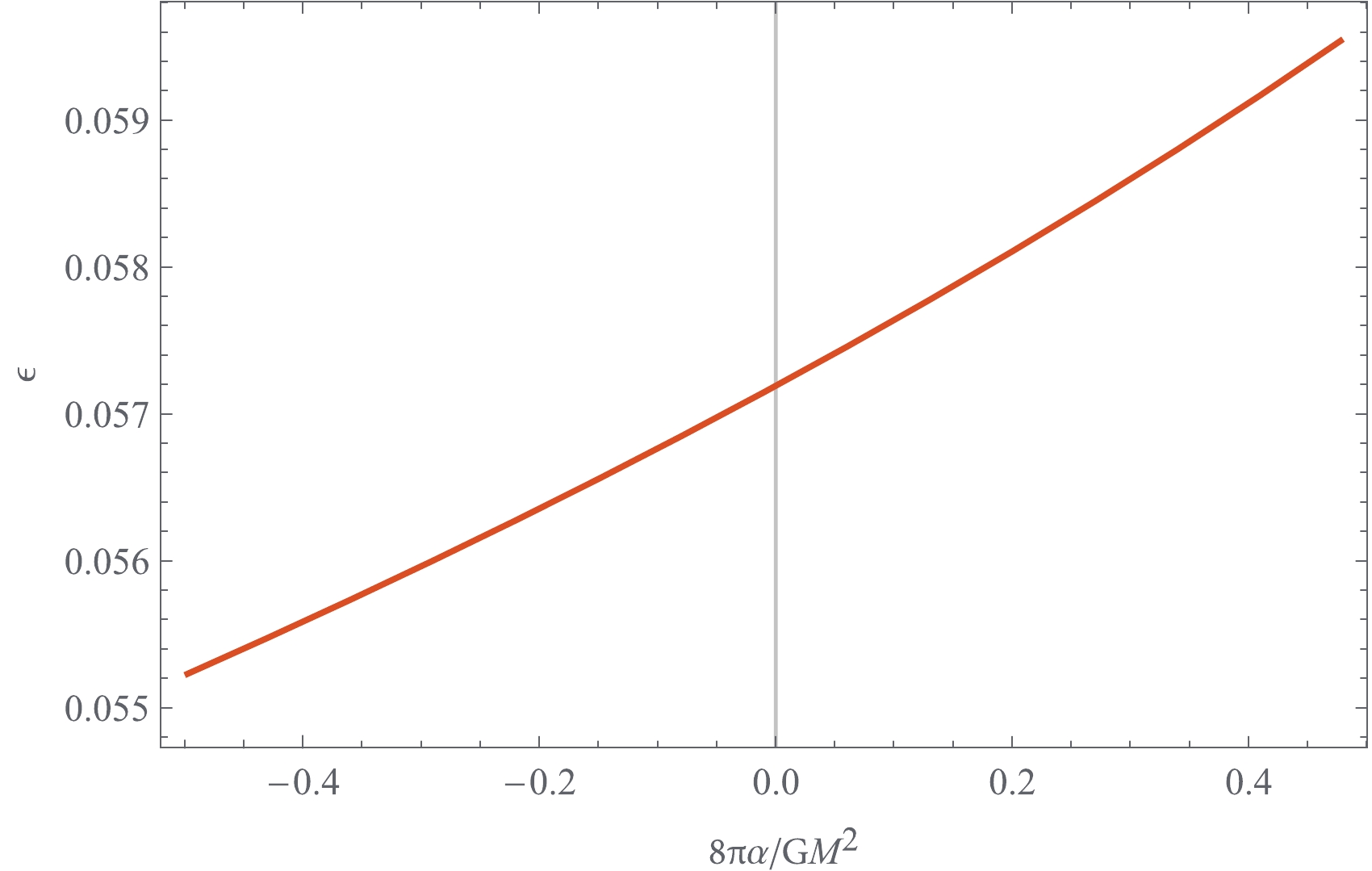
$ \epsilon $ is related to the specific energy of the moving particle in the disk, measured at the marginally stable orbit as$ \epsilon = 1- \tilde E_{\rm ms}. $

(45) The dependence of the accretion efficiency
$ \epsilon $ on the Gauss-Bonnet coupling constant$ \alpha $ is plotted in Fig. 6, which shows that the accretion efficiency$ \epsilon $ of the 4EGB black hole increases with increasing value of$ \alpha $ . This indicates that the accretion of matter in the 4EGB black hole is more efficient for positive$ \alpha $ and less efficient for negative$ \alpha $ than that in the Schwarzschild black hole. Therefore, the 4EGB black hole with positive Gauss-Bonnet coupling constant$ \alpha $ can provide a more efficient engine for transforming the energy of accreting matter into electromagnetic radiation than that with a negative value of$ \alpha $ . -
The recently proposed 4EGB theory of gravity includes a Gauss-Bonnet curvature correction to the Einstein term with a coupling constant proportional to
$ \alpha/(D-4) $ in the limit$ D\to 4 $ . With this formulation, the 4EGB gravity can make a non-trivial contribution to the gravitational dynamics in the limit$ D \to 4 $ . Several variants of this theory have been explored recently, and they have the same static, spherically symmetric black hole solution. In this paper, we study the physical properties of a thin accretion disk around a static spherically symmetric black hole in 4EGB gravity. The physical quantities of the thin accretion disk, such as the energy flux, temperature profile, electromagnetic emission spectrum profiles, and accretion efficiency, have been analyzed in detail for the 4EGB black hole. The effects of the Gauss-Bonnet coupling constant$ \alpha $ on these physical quantities have been explicitly obtained. With an increase in the parameter$ \alpha $ , the energy flux, temperature distribution, and electromagnetic spectrum of the disk all increase. The main reason for this behavior is that for positive$ \alpha $ , the effect of the Gauss-Bonnet coupling constant$ \alpha $ decreases the radius of the marginally stable orbit, so that the lower limit of the integral in (41) becomes smaller, while for negative$ \alpha $ , the radius of the marginally stable orbit increases, so that the lower limit becomes larger. In addition, we also show that the accretion efficiency increases with the growth of the parameter$ \alpha $ . Our results indicate that the thin accretion disk around the static, spherically symmetric black hole in 4EGB gravity is hotter, more luminous, and more efficient than that around a Schwarzschild black hole with the same mass for positive$ \alpha $ , while it is cooler, less luminous, and less efficient for negative$ \alpha $ .In addition to the above main results, we would like to mention two directions that can be explored to extend our analysis. First, in this paper, we only focus on the static and spherically symmetric black hole case. It would be interesting to explore the behaviors of the electromagnetic emission spectrum profiles of the thin accretion disk around a rotating black hole in the 4EGB theory. However, construction of the rotating solution is not an easy task, and a rigorous rotating black hole has not yet been found via solving the field equation. Although there is an effective rotating solution generated from the static and spherically symmetric black hole using the Newman-Janis procedure [21, 26], it is still not clear whether this solution is an exact one that satisfies the field equation of the 4EGB theory. To explore the features of the electromagnetic emission spectrum with rotation effects, we prefer to find the rotating solution by solving the field equation; this will be considered in our future work.
Second, when the rotating solution is found, it would also be interesting to constrain the black hole parameters, including the angular momentum and the Gauss-Bonnet parameter
$ \alpha $ , using the observation spectra of the X-ray binaries. For example, using the continuum-fitting method [79], the angular momentum of stellar-mass black holes can be measured, and the deviations from Kerr can be constrained using the X-ray data from black hole binaries. At present, the observational constraints of the 4EGB theory primarily come from Refs. [36] and [37]. In [37], the authors have considered the constraints on$ \alpha $ from various physical systems, including solar system experiments, binary pulsars, and cosmological observations. The tightest constraints come from observations of the periapsis advance of the LAGEOS II satellite and from the observation of binary black hole systems, both of which lead to$ |16 \pi G \alpha|\lesssim 10^{10} m^2 $ . In [36], the authors obtain the constraints$ -7.78\times 10^{-16} \lesssim 16 \pi G \alpha H^2 \lesssim 3.33\times 10^{-15} $ , where H is the Hubble parameter, from the current observation of the speed of GWs measured by GW170817 and the gamma ray burst event GRB 170817A. Compared with these existing constraints, the X-ray binaries can provide a very different environment for testing the 4EGB theory and may be more sensitive to the strong gravity behavior of the 4EGB theory. We hope to address the above issues soon in future studies to possibly extend some of these results.
Thin accretion disk around a four-dimensional Einstein-Gauss-Bonnet black hole
- Received Date: 2020-04-22
- Accepted Date: 2020-08-16
- Available Online: 2021-01-15
Abstract: Recently, a novel four-dimensional Einstein-Gauss-Bonnet (4EGB) theory of gravity was proposed by Glavan and Lin [D. Glavan and C. Lin, Phys. Rev. Lett. 124, 081301 (2020)], which includes a regularized Gauss-Bonnet term using the re-scalaring of the Gauss-Bonnet coupling constant





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF
















 DownLoad:
DownLoad: