-
The naive quark model describes hadrons as
$ q\bar{q} $ mesons and$ qqq $ baryons. Since quarks and gluons are the fundamental degrees of freedom of QCD, if gluons can act as building blocks similar to quarks to build up hadrons, from a phenomenological perspective, there may exist glueballs that are purely made up of gluons and hybrids that are composed of quarks and gluons. Glueballs, hybrids, and multiquark states (tetraquarks, pentaquarks, etc.) are usually called exotic hadrons in contrast to conventional$ q\bar{q} $ mesons and$ qqq $ baryons. Exotic hadrons are long-standing topics of interest in theoretical and experimental studies of particle physics, especially with the discovery of numerous$ XYZ $ particles in the current era based on experimental investigations. These particles exhibit exotic properties in their production and decay processes and are potential candidates for exotic hadrons [1]. Given that$ q\bar{q}g $ hybrids are made up of a quark-antiquark pair and a gluon, the$ J^{PC} = 1^{-+} $ states are most interesting since this quantum number is prohibited in conventional$ q\bar{q} $ mesons. There have been many theoretical studies on hybrids from a phenomenological perspective and the lattice QCD approach. It was determined that the lowest$ 1^{-+} $ hybrid usually has a mass of approximately 1 GeV higher than the ground state vector meson with the same$ q\bar{q} $ component. For example, the mass of the$ 1^{-+} $ hybrid with light flavors was estimated to be approximately 1.9 GeV, whereas those of the strangeonium-like and the charmonium-like counterparts are approximately 2.1-2.3 GeV [2, 3] and 4.1-4.3 GeV [4], respectively. Reliable candidates for$ 1^{-+} $ hybrids have not been experimentally determined to date. The vector charmonium-like state$ Y(4260) $ (or$ \psi(4230) $ named by PDG 2018 [5]), due to its very different properties compared to the conventional charmonia and the closeness of its mass to that of the$ 1^{-+} $ $ c\bar{c}g $ hybrid, has a possible assignment of$ 1^{--} $ hybrid [6].$ \phi(2170) $ [5], also known as$ Y(2175) $ , was first observed as a result of the BABAR Collaboration in the initial-state-radiation process$ e^+e^- \to \gamma_{\rm{ISR}}\phi f_0(980) $ in 2006 [7] and was confirmed later by BES and Belle [8, 9]. The similarity of its property to$ Y(4260) $ also suggests a$ s\bar{s}g $ hybrid interpretation of$ \phi(2170) $ .Phenomenologically,
$ q\bar{q}g $ hybrids are usually studied in the constituent gluon model [10], in which the gluon acts as an effective degree of freedom, similar to constituent quarks in the quark model, or the flux tube model in which the gluon is taken as a transverse vibration mode of the flux-tube that binds the$ q\bar{q} $ pair [11]. For the hybrids with a heavy quark-anti-quark pair$ Q\bar{Q} $ , the gluonic excitations along the flux-tube are fast objects, such that in the Oppenheimer approximation [12-14], their distribution obeys cylinder symmetry along the$ Q\bar{Q} $ -axis, and their motion effects on the$ Q\bar{Q} $ can be taken as a centrifugal barrier, apart from the binding linear potential. Based on the hybrid potentials simulated from the lattice QCD, one can solve the Schrödinger equation for the$ Q\bar{Q} $ system to obtain predictions regarding the spectrum of hybrids with properly tuned parameters. There have also been phenomenological studies on heavy quarkonium-like hybrids in which gluonic excitations are treated in a mean field manner [15-17].Lattice QCD is an ab initio non-perturbative approach for the study of strong interactions in the low energy scale and is applied extensively to the investigation of hybrids [18-26]. The mass of the hybrids can be derived from the correlation functions of hybrid-like operators
$ \bar{q}{\vec \Gamma} q \circ \vec{B} $ , where$ \bar{q}q $ is the color octet,$ \vec{B} $ is the chromomagnetic field strength,$ \Gamma $ represents specific combinations of$ \gamma $ matrices, and the symbol$ \circ $ represents any possible summation of the spatial indices of$ \vec{\Gamma} $ and$ \vec{B} $ . A recent lattice calculation [4] revealed that there exists a$ \{1^{- -},(0,1,2)^{-+}\} $ charmonium-like supermultiplet with nearly degenerate masses of approximately 4.2-4.4 GeV, which overlaps strongly with the hybrid-like operators. This observation implies that these states may have similar internal dynamics, whereas the spin-spin coupling of the$ \bar{q}q $ and$ \vec{B} $ yields the different quantum numbers. In our previous work [27], the internal structure of this supermultiplet was investigated by calculating their Bethe-Salpeter (BS) wave functions based on the lattice QCD in the quenched approximation, in which the spatially extended interpolating field operators$ \bar{q}{\vec \Gamma} q(\vec{x},t) \circ \vec{B}(\vec{x}+{\vec r},t) $ are introduced in the Coulomb gauge, whose matrix element between the vacuum and a state is defined as the BS wave function. It was determined that the BS wave functions of the states in this multiplet are very similar and exhibit interesting nodal structures, which imply that the distance between the$ c\bar{c} $ and the$ \vec{B} $ operator is a meaningful dynamic variable for hybrids.In this work, we extend the aforementioned study strategy to strangeonium-like hybrids and focus on the
$ \{1^{- -},(0,1,2)^{-+}\} $ states, to determine if a situation similar to that of the$ c\bar{c}g $ hybrids can also occur for the$ s\bar{s}g $ states. In contrast, since the quantum numbers$ 1^{- -} $ and$ 0^{-+} $ are permitted by the$ q\bar{q} $ mesons, in these channels, we will also use the spatially extended$ s\bar{s} $ operators for the quark fields with spatial separations to extract the related BS wave functions, from which we can investigate the internal structure of these states. By comparison of these two kinds of BS wave functions, we may obtain useful information on the possible different formation pattern of hybrids from conventional mesons. For$ \phi(2170) $ , since it can be$ 3^3 S_1 $ ,$ 2^3 D_1 $ $ s\bar{s} $ , or a candidate for the vector$ s\bar{s}g $ hybrid, its properties will be discussed based on the results of this study.This work is organized as follows. Section II gives a detailed description of our lattice setup and the numerical strategy, including the construction of the spatially extended operators, the data analysis procedure, and the results of the spectrum and BS wave functions. The discussion and the comparison of our results with those of relevant phenomenological studies are presented in Section III. Section IV is an overall summary.
-
The pure gauge configurations are generated via the tadpole-improved gauge action [28, 29] on anisotropic lattices with an aspect ratio of
$ \xi = a_s/a_t = 5 $ , where$ a_s $ and$ a_t $ are the spatial and temporal lattice spacing, respectively. Two lattices$ L^3\times T = 16^3\times 160(\beta = 2.4) $ and$ 24^3\times 192(\beta = 2.8) $ with different lattice spacings are used to check the discretization artifacts. The parameters of the gauge ensembles are listed in Table 1, where the$ a_s $ values are determined from$ r_0^{-1} = 410(20) $ MeV. For the strange valence quark, we use the tadpole-improved clover action, whose parameters are carefully tuned by requiring the dispersion relations of the vector and pseudoscalar mesons to be reproduced [30]. As will be addressed in the following sections, we will use spatially extended operators to calculate the relevant correlation functions. Therefore, the configurations are first fixed to the Coulomb gauge based on the standard gauge fixing procedure used in lattice QCD studies before the quark propagators are computed. In this investigation, we work in the quenched approximation for which the effects of dynamical quarks are omitted. As such, two-particle scattering states will not appear in the spectrum.$\beta$ 

$\xi$ 

$a_s$ /fm

$La_s$ /fm

$L^3\times T$ 

$N_{\rm conf}$ 

2.4 5 0.222(2) 3.55 $16^3\times 160$ 

500 2.8 5 0.138(1) 3.31 $24^3\times 192$ 

200 Table 1. The input parameters for the calculation. Values of the coupling
$\beta$ , anisotropy$\xi$ , lattice spacing$a_s$ , lattice size, and number of measurements are listed.$a_s/r_0$ is determined by the static potential; the first error of$a_s$ is the statistical error, and the second one is due to the uncertainty of the scale parameter$r_0^{-1}=410(20)$ MeV. -
The major goal of this study is to investigate the inner structure of
$ s\bar{s}g $ hybrids of the quantum numbers$ J^{PC} = 1^{- -}, (0,1,2)^{-+} $ . We introduce two types of spatially extended operators as sink operators. The first type includes the following$ s\bar{s}g $ operators:$ \begin{aligned}[b] O^k_{1^{- -}}(r, t) =& \sum\limits_{{\vec x}, |{\vec r}| = r} {\bar s}^a({\vec x}, t)\gamma_5 s^b({\vec x}, t)B^{ab}_ k({\vec x}+{\vec r}, t), \\ O_{0^{-+}}(r, t) =& \sum\limits_{{\vec x}, |{\vec r}| = r} {\bar s}^a({\vec x}, t)\gamma_i s^b({\vec x}, t)B^{ab}_ i({\vec x}+{\vec r}, t), \\ O^k_{1^{-+}}(r, t) =& \sum\limits_{{\vec x}, |{\vec r}| = r} {\bar s}^a({\vec x}, t)\gamma_i s^b({\vec x}, t)B^{ab}_ j({\vec x}+{\vec r}, t)\varepsilon_{ijk}, \\ O^k_{2^{-+}}(r, t) =& \sum\limits_{{\vec x}, |{\vec r}| = r} {\bar s}^a({\vec x}, t)\gamma_i s^b({\vec x}, t)B^{ab}_ j({\vec x}+{\vec r}, t)|\varepsilon_{ijk}|, \end{aligned} $

(1) where
$ i,j,k = 1,2,3 $ are the spatial indices,$ a, b = 1,2,3 $ are color indices, and$ B_i^{ab} = \frac{1}{2}\varepsilon_{ijk}F^{ab}_{jk} $ is the chromomagnetic field strength. The summation over$ {\vec r} $ with the same distance r leads to the operators having correct quantum numbers. It should be noted that on a hypercubic spacetime latice, the spin$ J = 2 $ corresponds to$ T_2\oplus E $ where$ T_2 $ and E are the irreducible representations of the lattice symmetry group O, so the$ O_{2^{-+}}^k(r,t) $ are the three components of$ T_2 $ . Generally speaking, the masses of the$ T_2 $ state and the E state, which correspond to the same$ J = 2 $ state, are different by$ O(a_s^n) $ terms (here, the power n depends on the specific lattice setups). This difference vanishes in the continuum limit$ a_s\to 0 $ . In this work, we ignore the mass splitting due to the discretization effect and treat the mass of the$ T_2 $ state as an approximation of the$ J = 2 $ state, so we do not give the explicit expression of the E operators in Eq. (1). The possible ground hybrids in these four quantum numbers form a supermultiplet as expected. Obviously, the two constituent quarks are localized at the same space-time point, and the gluon component is placed at another space point. The BS wave function that we attempt to extract reflects the dynamics of these two parts.Since the quantum numbers
$ J^{PC} = 0^{-+}, 1^{- -} $ are conventional ones for$ q\bar{q} $ mesons, we also introduce the second type of spatially extended$ s\bar{s} $ operators by splitting the strange quark field s and its conjugate$ \bar{s} $ by the spatial separation$ \vec{r} $ . This is explicitly expressed as$ \begin{aligned}[b] P_{0^{-+}}(r,t) =& \sum\limits_{{\vec x}, |{\vec r}| = r} {\bar s}({\vec x}, t)\gamma_5 s({\vec x}+{\vec r}, t) , \\ P^k_{1^{- -}}(r,t) =& \sum\limits_{{\vec x}, |{\vec r}| = r} {\bar s}({\vec x}, t)\gamma_k s({\vec x}+{\vec r}, t), \end{aligned} $

(2) where the summation over
$ \vec{r} $ with$ |\vec{r}| = r $ is performed to guarantee the correct$ J^{PC} $ .In practice, we calculate the wall-source correlation functions of these operators. For example, we use the following wall-source operators for
$ 1^{-+} $ states:$ O^{W,k}(\tau) = \sum\limits_{{\vec y},{\vec z}} {\bar s}^a({\vec y}, \tau)\gamma_i B^{ab}_ j({\vec z}, \tau) s^b({\vec z}, \tau)\varepsilon_{ijk}, $

(3) where
$ \tau $ indicates the source time slice. The wall-source operators for other$ J^{PC} $ states vary accordingly. The wall source operators for the$ s\bar{s} $ operators are$ P^{W}(\tau) =$ $ \displaystyle\sum\limits_{\vec{y},\vec{z}}\bar{s}(\vec{y},\tau)\Gamma s(\vec{z},\tau) $ with$ \Gamma = \gamma_5, \gamma_i $ for$ 0^{-+} $ and$ 1^{- -} $ , respectively. Finally, we calculate the correlation functions (for simplicity, we set$ \tau = 0 $ and omit the subscripts and superscripts that refer to specific symmetry channels and different spatial components) as$ C(r, t) = \langle O^k(r,t)O^{W,k\dagger}(0) \rangle. $

(4) After the intermediate state insertion, the correlation function
$ C(r,t) $ can be parameterized as$ \begin{aligned}[b] C(r,t) =& \frac{1}{N_c}\sum\limits_n \frac{1}{2m_nL^3}\langle 0| O(r,t) |n\rangle \langle n|O^W(0)|0\rangle \\ =& \frac{1}{N_c}\sum\limits_n \frac{1}{2m_nL^3}\langle 0| O(r,0) |n\rangle \langle n|O^W(0)|0\rangle {\rm e}^{-m_nt} \\ \equiv & \sum\limits_n \Phi_n(r) {\rm e}^{-m_nt} , \end{aligned} $

(5) where
$ N_c $ is the degenerate degree of$ r = |\vec{r}| $ ,$ m_n $ is the mass of the n-th state, and$ \Phi_n(r) $ is defined as the corresponding Bethe-Salpeter wave function up to an irrelevant constant factor. It should be noted that$ m_n $ is independent of r, so that if we simultaneously fit$ C(r,t) $ with different r using Eq. (5), we can obtain$ m_n $ and$ \Phi_n(r) $ . To be specific, if$ n_r $ different$ C(r,t) $ values with different r values are considered, and N mass terms are involved in the fitting model, the number of parameters to be fitted is$ N\cdot n_r+N $ . Since we usually have 20-30 statistically meaningful data points for each$ C(r,t) $ , the number of degrees of freedom is large enough in the fitting procedure. -
We start with the
$ 1^{-+} $ channel, since$ J^{PC} $ is a typical exotic quantum number which cannot be assigned to a$ q\bar{q} $ meson in the quark model. After the correlation function$ C(r,t) $ is calculated for the$ \beta = 2.4 $ and$ \beta = 2.8 $ lattices, Eq. (5) is used for data analysis wherein we use$ N = 3 $ mass terms. For the$ \beta = 2.4 $ lattice, the r range is from 0 to$ 0.9 $ fm (converted using the lattice spacing$ a_s $ in Table 1), and the upper limit of the fit window$ [t_{\rm{min}},t_{\rm{max}}] $ is uniformly set to be$ t_{\rm{max}} = 20 $ for all the$ C(r,t) $ , while the$ t_{\rm{min}} $ varies from 6 to 3. For the$ \beta = 2.8 $ lattice, r has a value up to$ 0.8 $ fm, and$ t_{\rm{max}} $ is set to$ t_{\rm{max}} = 30 $ , with$ t_{\rm{min}} $ varying from 9 to 6. For each lattice, we perform a simultaneous correlated fit for all the different$ C(r,t) $ values using the jackknife covariance matrix. Table 2 summarizes the fit results for the mass$ m_n $ with$ n = 1,2,3 $ for different time windows$ [t_{\rm{min}},t_{\rm{max}}] $ as well as$ \chi^2 $ per degree of freedom ($ \chi^2/{\rm{dof}} $ ), which is approximately one and indicates that the fits are reasonable. The mass of the lowest three states is stable to some extent for different$ t_{\rm{min}} $ and as such is a reliable parameter. For the lowest two states, the mass values for the$ \beta = 2.4 $ lattice are slightly larger (approximately 100 MeV larger) than those for$ \beta = 2.8 $ lattice. This difference might be attributed to the finite lattice spacing effect, and the strange quark mass parameters on the two lattices are not tuned to be exactly the same in the sense of their physical meaning. Combining the results from the two lattices, we can determine that the mass of the lowest$ 1^{-+} $ $ s\bar{s}g $ state is approximately 2.2 GeV. However, the mass splitting of the lowest two states is approximately 1.4 GeV, which is almost the same as that of the$ 1^{-+} $ charmonium-like hybrids, and thus exhibits quark mass independence to some extent.$t_{\rm{min}}$ 

$\chi^2/{\rm{dof}}$ 

$m_1$ /GeV

$m_2$ /GeV

$m_3$ /GeV

$\beta=2.4$ 

$t_{\rm{max}}=20$ 

( $s\bar{s}g$ )

6 1.12 2.232(22) 3.56(21) 7.5(2.7) 5 1.23 2.228(22) 3.61(26) 4.9(7) 4 1.36 2.248(13) 3.71(11) 5.7(5) 3 1.38 2.255(09) 3.65(07) 5.4(2) $\beta=2.8$ 

$t_{\rm{max}}=30$ 

( $s\bar{s}g$ )

9 1.53 2.099(16) 3.55(07) 7.7(7) 8 1.41 2.168(15) 3.78(13) 5.1(3) 7 1.47 2.100(15) 3.40(07) 5.8(2) 6 1.26 2.110(13) 3.47(06) 5.5(1) Table 2. The fitted masses
$m_n$ of the$1^{-+}$ states with$n=1,2,3$ from different time windows$[t_{\rm{min}},t_{\rm{max}}]$ and$\chi^2$ per degree of freedom ($\chi^2/{\rm{dof}}$ ) for the$\beta=2.4$ and$\beta=2.8$ lattices. All the masses are converted to values in physical units using the lattice spacing$a_s$ in Table 1.Along with the masses, the BS wave functions of the states of
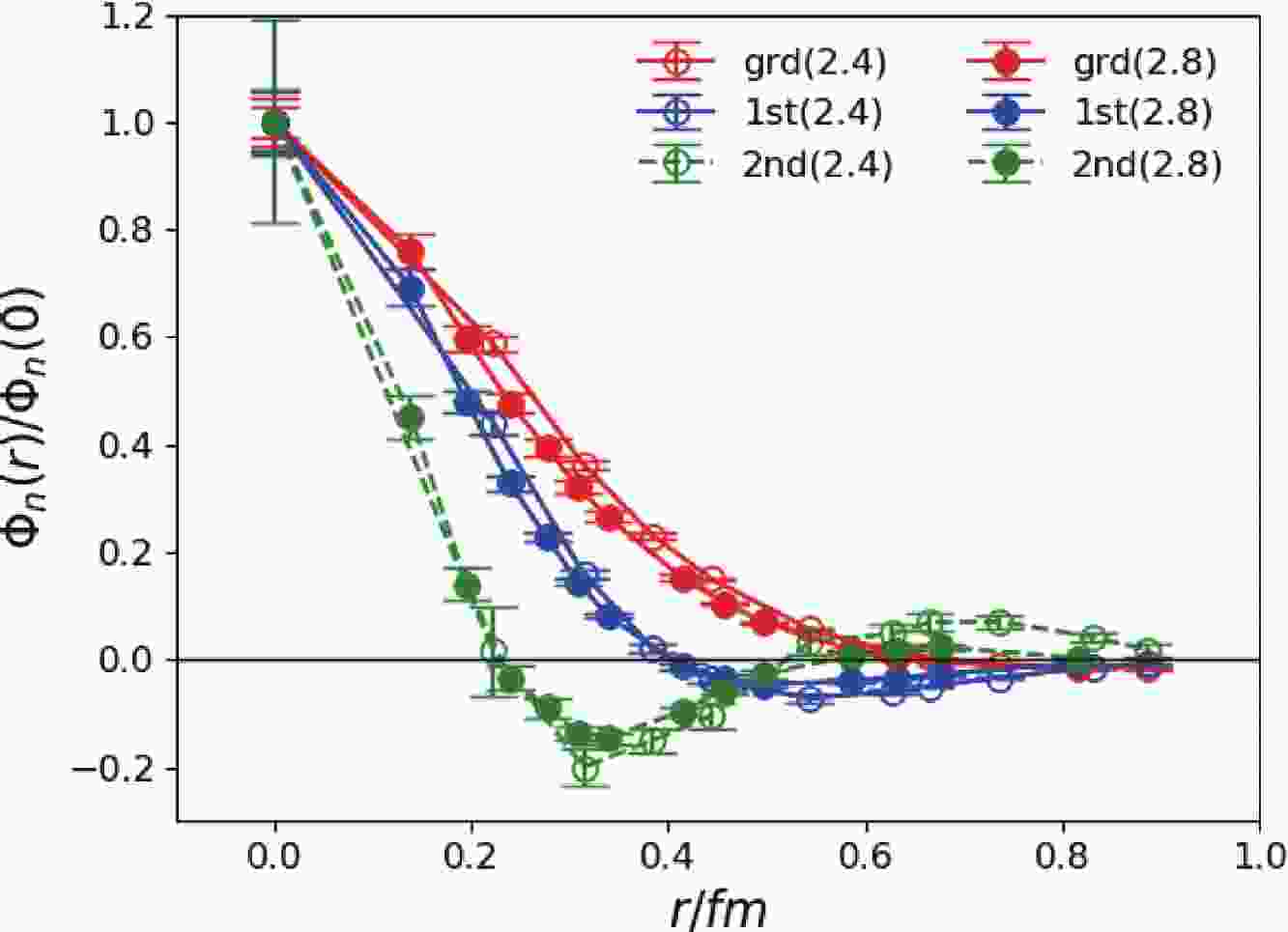
$ \Phi_n(r) $ can be extracted from the joint fit to$ C(r,t) $ as shown in Fig. 1. The radial separation r is converted to the value in physical units, and the wave functions on the two lattices are compatible with each other. The BS wave functions exhibit a clear nodal structure along the r direction: the BS wave function$ \Phi_1(r) $ of the ground state has no radial node, and that of the first excited state ($ \Phi_2(r) $ ere) has one node, whereas that of the third state has two nodes. These nodal structures are very similar to the non-relativistic two-body Schrödinger wave functions in a central potential. It should be noted that r is the spatial separation between the$ s\bar{s} $ component and the color chromomagnetic field strength$ \vec{B} $ . The r behavior of the wave functions of the excitations may imply that within the$ 1^{-+} $ $ s\bar{s}g $ hybrid, the relative movement between the$ s\bar{s} $ and the gluonic degrees of freedom can be viewed qualitatively as a two-body system in which r is a physically meaningful dynamic variable. The same data analysis strategy is applied to the$ 2^{-+} $ channel. The fitted masses of the lowest three states are listed in Table 3, and the wave functions are shown in Fig. 2. In comparison with the case of$ 1^{-+} $ , the masses of the$ 2^{-+} $ states are slightly higher (100-200 MeV higher for the ground states) than their$ 1^{-+} $ counterparts, but the pattern of the spectrum is similar. For the BS wave functions, the r behavior of the$ 1^{-+} $ and$ 2^{-+} $ states are similar. These observations support the assertion that the$ 1^{-+} $ and$ 2^{-+} $ states have almost the same inner structure and dynamics, whereas the small mass difference can be attributed to the different coupling between the spin of the$ s\bar{s} $ subsystem and the gluonic degrees of freedom. This meets our expectation that$ 1^{-+} $ and$ 2^{-+} $ states with the nearly degenerate mass can be in the same supermultiplet. Of course, the possibility exists that these$ 2^{-+} $ states can be the conventional$ s\bar{s} $ mesons since$ J^{PC} = 2^{-+} $ is permitted for a$ q\bar{q} $ system. However, the masses we obtain are much higher than those of the$ {}^1 D_2 $ $ s\bar{s} $ states in the quark model. However, a previous lattice study [31] on charmonium states found that the$ 2^{-+} $ $ c\bar{c}g $ operator couples almost exclusively to a state with a mass of 4.4 GeV instead of the expected$ 1^1D_2 $ charmonium state$ \eta_{c2} $ , with a mass of approximately 3.8 GeV. If this is also the case for the$ s\bar{s} $ states, the hybrid assignment is favorable for the$ 2^{-+} $ states we obtain in this work.
Figure 1. (color online) The BS wave functions
$\Phi_n(r)$ (normalized as$\Phi_n(0)=1$ ) of the lowest two$1^{-+}$ states. r is the spatial separation between the$s\bar{s}$ component and the chromomagnetic operator$B_i$ and is converted to the value in physical units. Open and filled data points are the results for$\beta=2.4$ and$\beta=2.8$ , respectively.
Figure 2. (color online) The BS wave functions
$\Phi_n(r)$ (normalized as$\Phi_n(0)=1$ ) of the lowest two$2^{-+}$ states. r is the spatial separation between the$s\bar{s}$ component and the chromomagnetic operator$B_i$ and is converted to the value in physical units. Open and filled data points are the results for$\beta=2.4$ and$\beta=2.8$ , respectively.$t_{\rm{min}}$ 

$\chi^2/{\rm{dof}}$ 

$m_1$ /GeV

$m_2$ /GeV

$m_3$ /GeV

$\beta=2.4$ 

$t_{\rm{max}}=20$ 

( $s\bar{s}g$ )

6 1.27 2.416(41) 3.65(23) 7.2(2.4) 5 1.37 2.406(41) 3.60(25) 5.5(8) 4 1.47 2.442(26) 3.69(19) 4.9(3) 3 1.56 2.426(19) 3.60(10) 5.0(1) $\beta=2.8$ 

$t_{\rm{max}}=30$ 

( $s\bar{s}g$ )

9 1.47 2.361(23) 3.89(09) 12.2(2.4) 8 1.24 2.321(34) 3.64(18) 5.5(5) 7 1.37 2.341(27) 3.71(12) 6.0(3) 6 1.40 2.359(19) 4.00(08) 6.2(2) Table 3. The fitted masses
$m_n$ of the$2^{-+}$ states with$n=1,2,3$ for different time windows$[t_{\rm{min}},t_{\rm{max}}]$ and$\chi^2$ per degree of freedom ($\chi^2/{\rm{dof}}$ ) for the$\beta=2.4$ and$\beta=2.8$ lattices. All the masses are converted to the values in physical units using the lattice spacing$a_s$ in Table 1. -
The
$ 0^{-+} $ and$ 1^{- -} $ states have conventional quantum numbers for$ q\bar{q} $ mesons, and the mesons with these quantum numbers are usually assigned to the$ n^1S_0 $ and$ n^3S_1 $ states in the quark model. Therefore, we start with the analysis of the wall-source correlation function$ C(r,t) $ of the$ s\bar{s} $ operators with the s and the$ \bar{s} $ field separated by a spatial distance r. We also use the function form of Eq. (5) with$ N = 3 $ mass terms. The upper bound of the fit window is fixed to$ t_{\rm{max}} = 40 $ and 30, and the lower bound gradually decreases to$ t_{\rm{min}} = 5 $ and 7 for$ \beta = 2.4 $ and$ \beta = 2.8 $ , respectively. The fitted masses of the$ 1^{- -} $ states are listed in Table 4 and those of the$ 0^{-+} $ states are listed in Table 5. As previously indicated, we use the physical mass of$ \phi(1020) $ to set the mass parameters of the strange quark in the fermion action on the two lattices with smaller gauge ensembles. However, the fitted mass of the ground state deviates from the physical mass slightly, which means that the strange quark masses are not tuned with sufficient precision. Therefore, one should consider this slight deviation when examining the data in the tables.$t_{\rm{min}}$ 

$\chi^2/{\rm{dof}}$ 

$m_1$ /GeV

$m_2$ /GeV

$m_3$ /GeV

$\beta=2.4$ 

$t_{\rm{max}}=40$ 

( $s\bar{s}$ )

8 0.84 1.013(1) 1.753(77) 2.16(22) 7 0.81 1.013(1) 1.787(93) 2.08(19) 6 0.83 1.014(1) 1.732(47) 2.13(12) 5 0.92 1.015(1) 1.709(36) 2.11(08) $\beta=2.4$ 

$t_{\rm{max}}=45$ 

( $s\bar{s}g$ )

16 1.40 1.011(1) 1.72(12) — 15 1.42 1.011(1) 1.66(10) — 14 1.42 1.009(1) 1.77(08) — 13 1.67 1.007(1) 1.83(06) — $\beta=2.8$ 

$t_{\rm{max}}=30$ 

( $s\bar{s}$ )

10 1.93 1.001(5) 1.634(114) 2.17(29) 9 1.97 1.003(4) 1.633(86) 2.02(18) 8 2.11 0.999(3) 1.665(81) 2.30(20) 7 2.39 0.998(3) 1.668(52) 2.34(17) $\beta=2.8$ 

$t_{\rm{max}}=45$ 

( $s\bar{s}g$ )

19 1.17 1.006(4) 1.51(6) — 18 1.39 1.003(3) 1.55(6) — 17 1.50 1.005(3) 1.51(5) — 16 1.45 0.998(2) 1.58(4) — Table 4. The fitted masses
$m_n$ of the$1^{--}$ states for two different types of operators and different time windows$[t_{\rm{min}},t_{\rm{max}}]$ and$\chi^2$ per degree of freedom ($\chi^2/{\rm{dof}}$ ) for the$\beta=2.4$ and$\beta=2.8$ lattices. All the masses are converted to values in physical units using the lattice spacing$a_s$ in Table 1.$t_{\rm{min}}$ 

$\chi^2/{\rm{dof}}$ 

$m_1$ /GeV

$m_2$ /GeV

$m_3$ /GeV

$\beta=2.4$ 

$t_{\rm{max}}=40$ 

( $s\bar{s}$ )

8 0.70 0.7012(2) 1.690(34) 2.21(17) 7 0.69 0.7010(2) 1.698(39) 2.12(14) 6 0.73 0.7010(2) 1.699(30) 2.12(10) 5 0.89 0.7014(2) 1.669(22) 2.10(07) $\beta=2.4$ 

$t_{\rm{max}}=45$ 

( $s\bar{s}g$ )

16 1.30 0.7008(3) 1.711(73) — 15 1.40 0.7007(3) 1.680(56) — 14 1.42 0.7007(3) 1.672(46) — 13 1.56 0.7009(3) 1.659(36) — $\beta=2.8$ 

$t_{\rm{max}}=30$ 

( $s\bar{s}$ )

10 2.59 0.6483(8) 1.736(62) 2.84(34) 9 2.51 0.6505(8) 1.703(76) 2.33(25) 8 2.37 0.6512(8) 1.679(66) 2.23(20) 7 2.35 0.6516(7) 1.620(30) 2.46(11) $\beta=2.8$ 

$t_{\rm{max}}=45$ 

( $s\bar{s}g$ )

19 1.09 0.6508(10) 1.621(85) — 18 1.03 0.6510(10) 1.557(67) — 17 1.04 0.6490(06) 1.711(50) — 16 1.06 0.6491(05) 1.740(39) — Table 5. The fitted masses
$m_n$ of the$0^{-+}$ states for two different types of operators and different time windows$[t_{\rm{min}},t_{\rm{max}}]$ and$\chi^2$ per degree of freedom ($\chi^2/{\rm{dof}}$ ) for the$\beta=2.4$ and$\beta=2.8$ lattices. All the masses are converted to values in physical units using the lattice spacing$a_s$ in Table 1.In the
$ 1^{- -} $ channel, the masses of the ground state and the first excited state are approximately 1 GeV and 1.7 GeV, respectively, which are compatible with those of$ \phi(1020) $ and$ \phi(1680) $ . For the$ \beta = 2.4 $ lattice, the fitted mass$ m_3 $ of the third state is also stable with respect to$ t_{\rm{min}} $ , and the value is approximately 2.1 GeV, which is close to the expected mass of the$ 3^3S_1 $ state for the quark model. The$ m_3 $ on the$ \beta = 2.8 $ lattice is also in this mass range but fluctuates more strongly with$ t_{\rm{min}} $ .In the
$ 0^{-+} $ channel, the ground state mass can be precisely determined with$ m_1\approx 0.701 $ GeV at$ \beta = 2.4 $ and$ 0.651 $ GeV at$ \beta = 2.8 $ . Since the$ s\bar{s} $ pseudoscalar meson (labeled as$ \eta_s $ ) is not a physical state, we cannot directly compare our result to the physical value . A previous calculation has been performed for the$ N_f = 2+1 $ full-QCD lattice formalism, which gives the prediction$ m_{\eta_s} = 0.686(4) $ GeV [32], lying between our values for the two lattices. The deviation is small and can be attributed to our less precise tuning of the strange quark mass parameter and the other systematic uncertainties. The mass of the first excited state is approximately 1.6-1.7 GeV, which is almost degenerate with that of the first excited$ 1^{- -} $ state. There is no physical correspondence of this state at present, but it can be compared to the pseudoscalar$ \eta(1295)/\eta(1475) $ . However, it should be noted that this state is a pure$ s\bar{s} $ state, which results in a higher mass. As indicated in the previous section, the BS wave functions$ \Phi_n(r) $ of the$ 0^{-+} $ and$ 1^{- -} $ states can be derived simultaneously with the masses, as shown in Figs. 3 and 4. It should be noted that r represents the separation between the s and$ \bar{s} $ field. For the ground state and the first excited state in each channel, the$ \Phi_n(r) $ values exhibit the expectation of the quark model in that the wave function of the ground state has no radial node whereas that of the first excited state has one node. Therefore, the two states can be assigned to be the$ 1S $ and$ 2S $ states of a non-relativistic$ s\bar{s} $ system. The behavior of the wave function of the third state is strange in that it has no radial nodes even though it has two inflection points. Since we only use three mass terms to fit the correlation functions, the third state may have substantial contamination from higher states, which may result in this phenomenon. As such, the results of the third state are not seriously considered.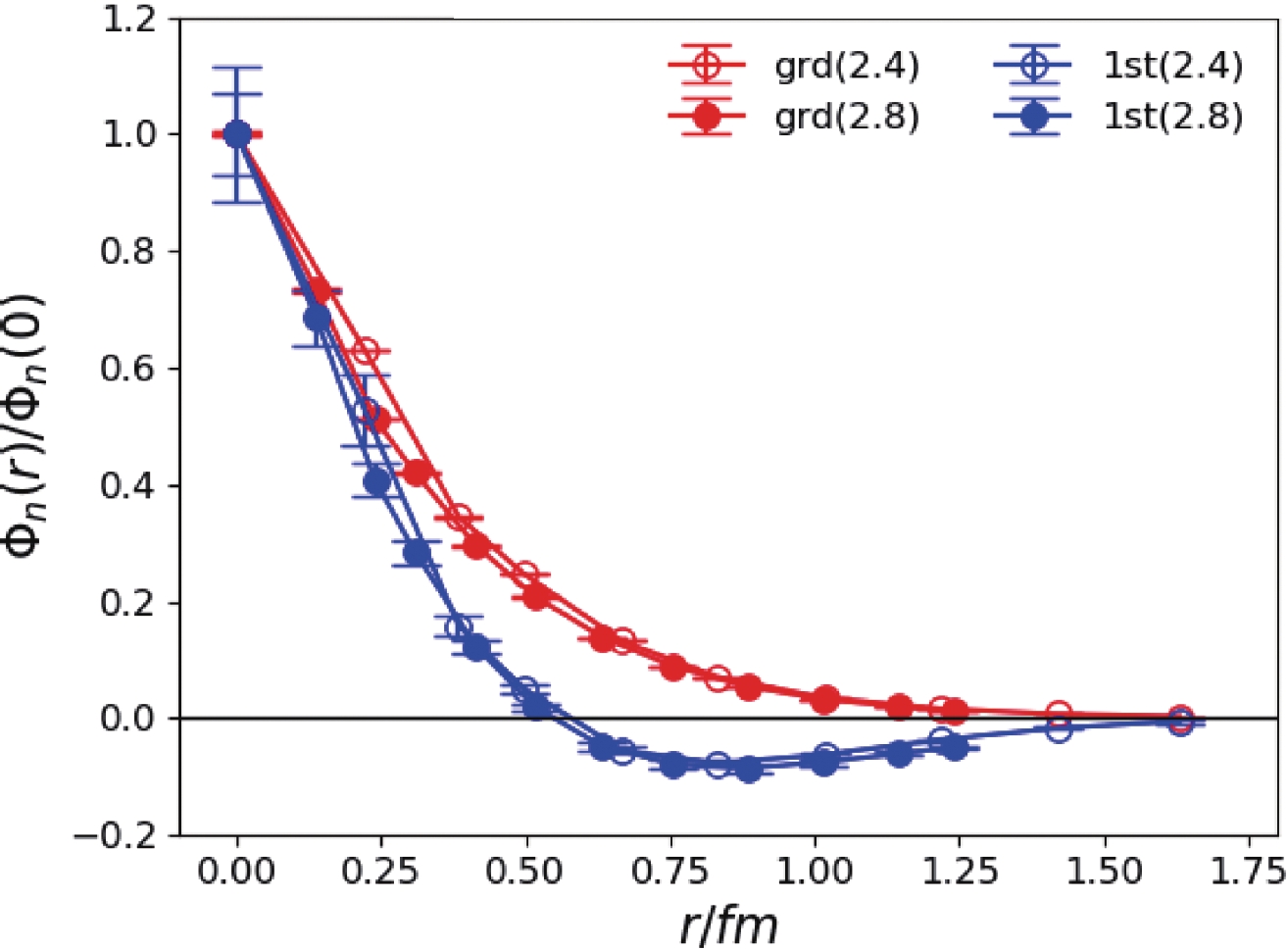
Figure 3. (color online) The BS wave functions
$\Phi_n(r)$ (normalized as$\Phi_n(0)=1$ ) of the lowest two$0^{-+}$ states. r is the spatial separation between the quark fields s and$\bar{s}$ and is converted to the value in physical units. Open and filled data points are the results for$\beta=2.4$ and$\beta=2.8$ , respectively.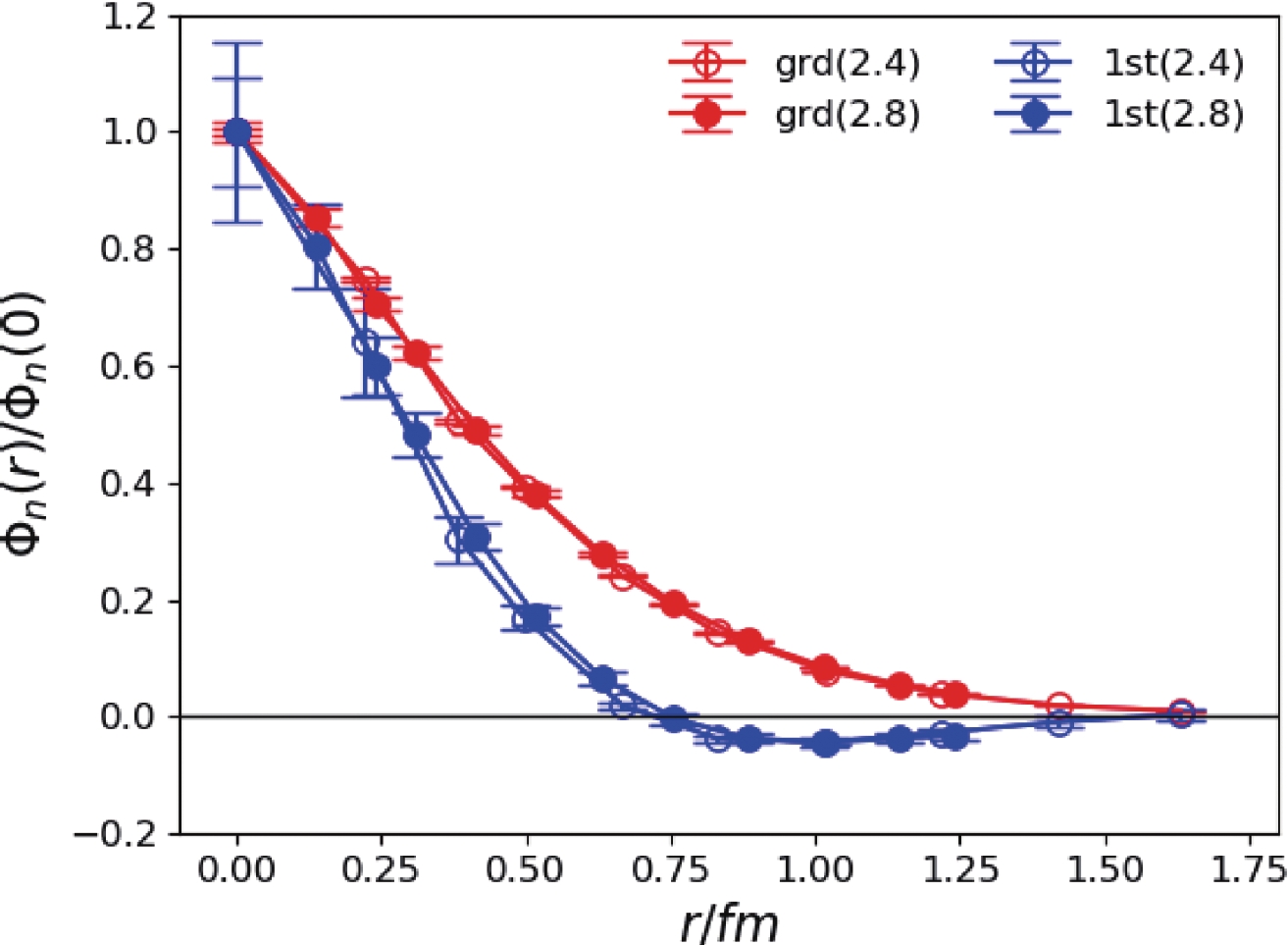
Figure 4. (color online) BS wave functions
$\Phi_n(r)$ (normalized as$\Phi_n(0)=1$ ) of the lowest two$1^{--}$ states. r is the spatial separation between the quark fields s and$\bar{s}$ and is converted to the value in physical units. Open and filled data points are the results for$\beta=2.4$ and$\beta=2.8$ , respectively.We also use the
$ s\bar{s}g $ -type operators (in Eq. (1)) to explore the properties of the$ 0^{-+} $ and$ 1^{- -} $ states. We use Eq. (5) with$ N = 2 $ mass terms to fit the correlation functions in large time ranges ($ t_{\rm{max}} = 45 $ for both lattices). The masses are listed in Table 4 and Table 5, in which it is apparent that they are consistent with those from the$ s\bar{s} $ operators. Figures 5 and 6 show the BS wave functions with r as the spatial separation between the$ s\bar{s} $ components and the chromomagnetic operator. The results for the two lattices are compatible with each other. It is interesting to see that for the$ 0^{-+} $ and$ 1^{- -} $ channels, such wave functions of the ground state ($ 1S $ state) and the first excited state ($ 2S $ state) lie almost upon each other and there are no significant differences. In these two channels, given the masses that are compatible with the masses of the states obtained using the$ s\bar{s} $ operators, the ground states and the first excited states can be assigned to the$ 1S $ and$ 2S $ $ s\bar{s} $ mesons. As such the similarity of the wave functions of$ 1S $ and$ 2S $ states with respect to the distance r between the gluonic component and the$ s\bar{s} $ component can be interpreted as follows: the s (or$ \bar{s} $ ) field along with the chromomagnetic field can be viewed as a dressed$ s' $ (or$ \bar{s}' $ ) field in the fundamental representation of the color$ SU(3) $ group, which annihilates the s (anti)quark of the$ s\bar{s} $ meson. In this sense, r represents the spatial size of the dressed quark field and the r fall-off does not have a dynamic significance. This is in contrast to the wave functions of the$ 1^{-+} $ and$ 2^{-+} $ states whose nodal structures imply that r is a dynamic variable for hybrids.
Figure 5. (color online) The BS wave functions
$\Phi_n(r)$ (normalized as$\Phi_n(0)=1$ ) of the lowest two$1^{--}$ states. r is the spatial separation between the$s\bar{s}$ component and the chromomagnetic operator$B_i$ and is converted to the value in physical units. Open and filled data points are the result for$\beta=2.4$ and$\beta=2.8$ , respectively. Since the two states can be assigned to be the$1S$ and$2S$ $s\bar{s}$ mesons, the similar r-behavior of their BS wave functions imply that this r is not a typical dynamical variable for the$s\bar{s}$ states.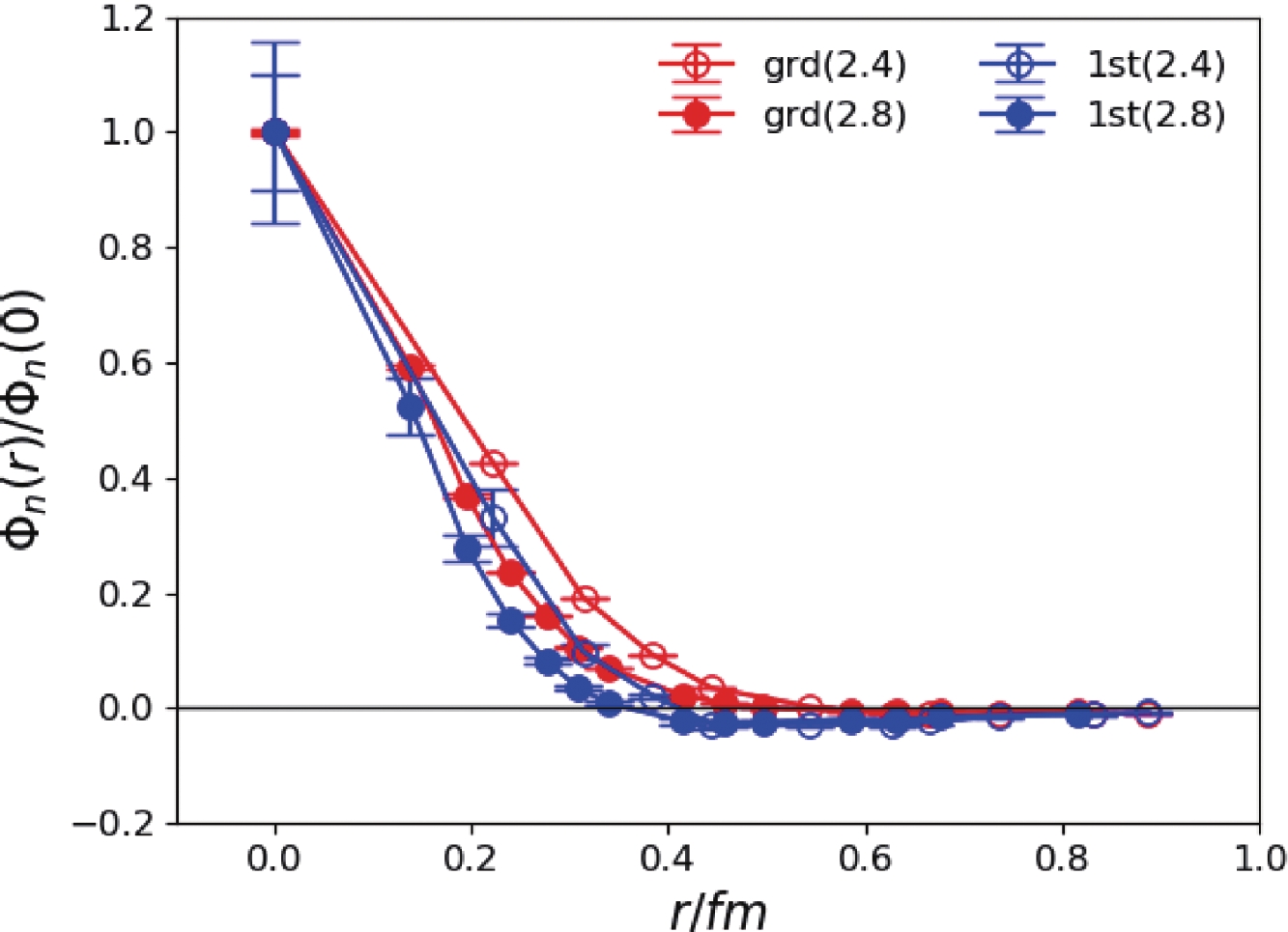
Figure 6. (color online) Similar to Fig. 5 but for
$0^{-+}$ states. -
We discuss the obtained results in this section. The BS wave functions of the
$ 1^{-+} $ and$ 2^{-+} $ states show the typical behaviors of non-relativistic two-body Schrödinger wave functions with a central potential, in terms of the correspondence of the spectrum and the nodal structure of the wave functions. We emphasize that the variable r is the spatial distance between the$ s\bar{s} $ component and the chromomagnetic field strength of the operators. Since$ 1^{-+} $ is an exotic quantum number for$ q\bar{q} $ mesons, the states with this quantum number must be a hybrid meson with additional gluonic degrees of freedom. The similarity of the spectrum and the wave functions of the$ 2^{-+} $ states to those of the$ 1^{-+} $ states indicates that they are also hybrid states. In this sense, the wave functions imply that r can be a meaningful dynamical variable for$ s\bar{s}g $ hybrid mesons. In a previous lattice study on$ c\bar{c}g $ hybrids [27], the same behaviors of the wave functions and the spectrum pattern were observed for the$ (0,1,2)^{-+} $ and$ 1^{- -} $ supermultiplets, based on which a "color halo" concept has been proposed, which states that a hybrid meson can be viewed as a relatively compact color octet$ q\bar{q} $ pair surrounded by color octet gluonic degrees of freedom, such that the wave functions depict the relative motion between the$ q\bar{q} $ pair and the gluonic excitation. In a non-relativistic model, the binding mechanism can be the potential between two effective color octet charges. Previous lattice studies [33] revealed that the potential of two static color charges has the feature of a Casimir scaling$ V_D(r) = V_{D,0}-C_D\frac{\alpha}{r} +\sigma_D r , $

(6) where D is the color
$ SU(3) $ representation of the charge with$ C_D $ as the eigenvalue of the second order Casimir operator of the color$ SU(3) $ ,$ V_{D,0} $ is the potential constant,$ \alpha $ is the coefficient of the Coulomb part, and$ \sigma_D $ is the string tension, which is related to the conventional string tension$ \sigma $ between a static quark and antiquark pair by$ \sigma_D = \frac{3}{4} C_D \sigma $ . For the octet charge in this work, this relation is$ \sigma_D = 9/4 \sigma $ , which means that the interaction between the color octet objects is stronger than that between the color triplet ones. This explains the observation that the mass splitting (approximately 1.2 GeV) between the ground state and the first excited hybrid state is larger than the$ 1S-2S $ mass splitting of the$ q\bar{q} $ states (approximately 0.6 GeV).The "color halo" idea is conceptually different from the flux-tube framework of hybrids in the market [12-14, 34, 35], whereby the quark and anti-quark are bound by an effective potential induced by the excitation of gluonic degrees of freedom. In the leading Born-Oppenheimer approximation, the
$ Q\bar{Q} $ of a heavy quarkonium-like hybrid can be viewed as static color sources; the excited gluonic degrees of freedom are distributed along the$ Q\bar{Q} $ axis and obey the cylinder symmetry, whose effect can be treated as an excited static potential denoted by$ \Lambda_\eta^\epsilon $ , where$ \Lambda = 0,1, 2,\ldots $ is the projected total angular momentum of the gluons with respect to the$ Q\bar{Q} $ axis and is labeled as$ \Sigma, \Pi, \Delta $ for$ \Lambda = 0,1,2 $ , and so on,$ \eta $ represents the combined parity (P) and the charge conjugate (C) of gluon excitations with$ \eta = g,u $ for$ P\otimes C = \pm $ , respectively, and$ \epsilon $ is the P parity of the glue state. Therefore, the quantum number of a$ Q\bar{Q} $ state with this potential is$ P = \epsilon (-1)^{L+\Lambda+1}, C = \eta\epsilon (-1)^{L+S+\Lambda} , $

(7) where
$ \hat{L} = \hat{L}_{Q\bar{Q}}+\hat{J}_g $ with$ \hat{L}_{Q\bar{Q}} $ being the orbital angular momentum of$ Q\bar{Q} $ with respect to the midpoint of the$ Q\bar{Q} $ axis and$ \hat{J}_g $ being the total angular momentum of the gluons. The ground$ \Sigma_g^+ $ potential has$ \Lambda = 0, \epsilon = + $ and$ \eta = + $ are the conventional static potential of$ Q\bar{Q} $ of the Cornell type, and the P and C quantum numbers reproduce the conventional quantum number. The$ 1^{- -} $ and$ (0,1,2)^{-+} $ hybrid supermultiplet is associated with the$ \Pi^+_u (L = 1) $ potential, such that the radial Shrödinger equation is$ \frac{{\rm d}^2}{{\rm d}r^2} u(r)+2\mu[E-V_{\rm{eff}}(r)]u(r) = 0 , $

(8) where r is the distance between Q and
$ \bar{Q} $ ,$ \mu $ is the reduced mass of the$ Q\bar{Q} $ pair, and$ u(r) $ is related to the radial wave function$ \phi(r) $ by$ u(r) = r\phi(r) $ . The effective potential$ V_{\rm{eff}} $ is$ V_{\rm{eff}} = V_{Q\bar{Q}}(r)+\frac{\langle \hat{L}_{Q\bar{Q}}^2\rangle}{2\mu r^2} $

(9) with
$ \langle \hat{L}_{Q\bar{Q}}^2\rangle = L(L+1)-2\Lambda^2+\langle \hat{J}_g^2\rangle $ and$ \langle \hat{J}_g^2\rangle = 2 $ . Obviously, the eigenvalues of E are independent of the total spin S of the$ Q\bar{Q} $ pair. One can use the lattice results to determine$ V_{Q\bar{Q}} $ and then solve the preceding equation to obtain the masses of the hybrids. We do not wish to delve into such details in this work but mention that$ \phi_n(r) $ behaves as a P-wave wave function in a central potential, and the mass splitting of the ground state and the first radial excited state is only a few hundred MeV for the$ 1^{- -} $ and$ (0,1,2)^{-+} $ hybrid states [14]. Even though the preceding deduction is based on the heavy quarkonium-like hybrids, this concept has been also applied to the phenomenological studies of strangeonium hybrids [34].In contrast to the flux-tube concept, we observe that for
$ (1,2)^{-+} $ strangeonium hybrids, the mass splitting of the ground and the first excited states is approximately 1.2-1.4 GeV, which is much larger than the prediction of the flux-tube model, and the nodal structure is present with respect to the spatial distance between the$ s\bar{s} $ and the chromomagnetic field strength. A similar phenomenon also appears for charmonium-like hybrids without a clear quark mass dependence. It should be emphasized that even though the interpretation of the wave functions is debatable, the pattern of the spectrum should be reliable and model-independent since it is derived directly from the lattice QCD calculation.For the
$ 0^{-+} $ and$ 1^{- -} $ channels, we obtain consistent results for the masses of the ground states and the first excited state using the$ s\bar{s} $ and$ s\bar{s}g $ type operators. Since we use the physical mass of the$ \phi(1020) $ meson to set the strange quark mass parameters, it is natural to almost reproduce the physical value of the mass of the vector ground state. The ground state mass of the pseudoscalar is approximately$ 650-700 $ MeV, which is compatible with the previous lattice result of$ \eta_s $ . The masses of the first excited states in both channels are closely degenerate at$ 1.7 $ GeV, and the mass of the first excited$ s\bar{s} $ vector meson is in agreement with that of$ \phi(1680) $ . However, the BS wave functions in both channels, defined based on the dependence of spatial distance between the s and$ \bar{s} $ quark field, show the expected radially nodal behavior of the non-relativistic$ s\bar{s} $ two-body system. Therefore, the ground and the first excited states can be assigned to be the$ 1S $ and$ 2S $ $ s\bar{s} $ mesons, respectively. We also obtain some information on the third state based on the$ s\bar{s} $ type operator in each channel, whose mass is approximately 2.1-2.3 GeV. For the vector channel, this mass value is close to the mass of$ \phi(2170) $ . However, since we only use three mass terms for the data fitting, the third state may have substantial contaminations from higher states, and the result is not reliable. When we use the$ s\bar{s}g $ operator to study these two channels, we can only obtain information on the lowest two states. At present, there is no definitive conclusion to whether there is a$ 1^{- -} $ and$ (0,1,2)^{-+} $ supermultiplet of the strangeonium hybrids.Finally, we present some arguments related to
$ \phi(2170) $ . Its mass is in the range of the$ 3^3S_1 $ and$ 2^3D_1 $ $ s\bar{s} $ predicted by the quark model. If a$ 1^{- -} $ and$ (0,1,2)^{-+} $ $ s\bar{s}g $ hybrid multiplet exists with nearly degenerate masses at approximately$ 2.1-2.3 $ GeV,$ \phi(2170) $ can also be a candidate for the$ 1^{- -} $ member. However, the assignment of its characteristic is still an open question. Till now,$ \phi(2170) $ has been observed in many final states including$ \phi(1020) $ , such as$ \phi f_0(980) $ ,$ \phi\pi\pi $ ,$ \phi \eta $ , and$ \phi \eta' $ . In the$ K^+K^-\pi\pi $ and$ K^+K^-K^+K^- $ final states [36-38], there are also sizable components including$ \phi(1020) $ . If$ \phi(2170) $ is a candidate for the$ 1^{- -} $ $ s\bar{s}g $ hybrid, this decay pattern can be understood based on the color halo concept of the hybrids: the binding between the color octet$ s\bar{s} $ and the gluonic degrees of freedom can easily break up such that the$ s\bar{s} $ component is neutralized to$ \phi(1020) $ and the gluons are hadronized to light hadrons, which are in the flavor singlet. Furthermore, in contrast to the hadronic transition of conventional excited strangeonium states, these decays are less OZI suppressed due to the existing gluons within the strangeonium hybrids. Recently, the BESIII Collaboration reported the observation of$ \phi(2170) $ in the process$ e^+e^-\to \eta'\phi $ with the resonance parameters$ M_R = 2177.5\pm $ $ 4.8({\rm{stat}})\pm 19.5({\rm{syst}}) $ MeV and$\Gamma_R = 149.0\pm 15.6({\rm{stat}})\pm $ $ 8.9({\rm{syst}}) $ MeV, and$ {\rm{Br}}(\phi(2170) \to \eta'\phi)\Gamma_{e^+e^-} $ is measured to be$ 7.1\pm 0.7({\rm{stat}})\pm 0.7({\rm{syst}}) $ eV [39]. Combining the result of$ {\rm{Br}}(\phi(2170) \to \eta\phi)\Gamma_{e^+e^-} = 1.7\pm 0.7({\rm{stat}})\pm 1.3({\rm{syst}}) $ eV, one has$ \frac{{\rm{Br}}(\phi(2170) \to \eta\phi)\Gamma_{e^+e^-}}{{\rm{Br}}(\phi(2170) \to \eta'\phi)\Gamma_{e^+e^-}} = 0.23\pm 0.10({\rm{stat}})\pm 0.18({\rm{syst}}). $

(10) This ratio is much larger than the predictions of phenomenological studies based on the flux tube model or the constituent gluon model of hybrids, with the mechanism whereby the flux tube or the constituent gluon breaks up into a light
$ q\bar{q} $ pair that reorganizes into two mesons with the original constituent$ s\bar{s} $ . However, this ratio can be explained directly from the flavor octet-singlet mixing and the kinetics. If$ \phi(2170) $ is a$ s\bar{s}g $ hybrid in the 'color halo' picture, then the decay$ \phi(2170)\to \phi\eta(\eta') $ can take place as follows: a gluon is emitted by a constituent strange quark (or antiquark) and the original gluon(s) couple to the flavor singlet component of the$ \eta(\eta') $ meson. If$ \phi(2170) $ is a higher excited$ s\bar{s} $ meson, then the$ \eta(\eta') $ is generated by two gluons emitted by the$ s\bar{s} $ pair. It should be noted that this process can be enhanced by the QCD axial anomaly. Since the decay dynamics is expected to be the same for the$ \phi\eta $ and$ \phi\eta' $ decay modes, the ratio of the partial widths can be attributed to the$ \eta-\eta' $ mixing and the kinetic factors$ \frac{\Gamma(\phi(2170)\to\phi\eta)}{\Gamma(\phi(2170)\to\phi\eta')} = \tan^2\theta \left(\frac{k_\eta}{k_{\eta'}}\right)^3 , $

(11) where
$ \theta $ is the flavor octet-singlet mixing angle of the$ \eta-\eta' $ system, and$ k_{\eta^{(')}} $ is the magnitude of the decay momentum. If we take the physical masses$ m_\eta = 547 $ MeV and$ m_{\eta'} = 958 $ MeV and the mixing angle$ \theta $ as varying between$ -10^\circ $ and$ -20^\circ $ , this ratio is estimated to be between$ 0.14 $ and$ 0.58 $ and compatible with the experimental value (the mixing angle$ \theta $ is derived to be approximately$ |\theta|\approx 13^\circ $ using the central value 0.23). As such, for$ \phi(2170) $ , this ratio may not be an ideal criterion to distinguish a hybrid assignment from a conventional$ s\bar{s} $ meson. Apart from the decay modes involving$ \phi(1020) $ , BESIII have reported$ K\bar{K} $ decay modes of resonances X observed in the procesess$ e^+e^-\to X\to K\bar{K} $ with a peak of X at approximately$ 2.2 $ GeV [38, 40]. For the characteristics of$ \phi(2170) $ to be revealed, all the observed decay modes should be considered jointly in scrutinized theoretical discussions. -
The strangeonium-like hybrids were investigated based on lattice QCD in the quenched approximation. Two anisotropic lattices with different lattice spacings were used to examine finite
$ a_s $ effects. We constructed spatially extended$ s\bar{s}g $ operators with the$ s\bar{s} $ component separated from the chromomagnetic field strength operator by a spatial distance r. We investigated the$ 1^{- -} $ and$ (0,1,2)^{-+} $ channels and calculated the corresponding correlation functions based on these operators in the Coulomb gauge. The ground state mass of the$ 1^{-+} $ states was determined to be 2.1-2.2 GeV and that of the$ 2^{-+} $ states was approximately 200 MeV higher. These results are consistent with previous lattice calculations and phenomenological studies. The masses of the first excited state were approximately 3.6 GeV in these two channels, such that the mass splitting of the first excited state and the ground state was approximately 1.2-1.4 GeV. This is much higher than the predictions obtained based on the flux-tube model, which is only a few hundred MeV. The BS wave functions of these states, defined by the matrix elements of the aforementioned operators between the vacuum and the states, were extracted and exhibit clear nodal structures in the r direction. This indicates that r is a meaningful dynamical variable reflecting the relative motion of the center-of-mass of the$ s\bar{s} $ against the gluonic degrees of freedom. Both the spectrum and the wave functions of these$ s\bar{s}g $ states have features similar to those of their$ c\bar{c}g $ counterparts and are consistent with the "color halo" concept of the hybrids in that the color octet$ q\bar{q} $ pair is surrounded by gluons.In the
$ 0^{-+} $ and$ 1^{- -} $ channels, we used both the spatially extended$ s\bar{s} $ and$ s\bar{s}g $ operators to perform the calculations. The ground state mass of the vector$ s\bar{s} $ meson almost reproduced the mass of$ \phi(1020) $ (it should be noted that we use the mass of the$ \phi(1020) $ to set the strange quark mass parameters), and the ground state mass of the pseudoscalar was 650-700 MeV, which is in agreement with the$ \eta_s $ mass determined by previous lattice calculations. In both channels, the masses of the first excited states were almost degenerate at approximately 1.7 GeV and compatible with the mass of$ \phi(1680) $ . The BS wave functions of these states with respect to the distance between s and$ \bar{s} $ were qualitatively similar to the nonrelativistic wave function of a two-body system in that the BS wave function of the first excited state had a radial node. Therefore, the first excited state can be a$ 2S $ $ s\bar{s} $ meson. In contrast, in each channel, the BS wave functions with respect to the spatial distance of the octet$ s\bar{s} $ and the gluonic degrees of freedom had similar profiles for the ground and the first excited state, which meant that this distance was less significant for$ s\bar{s} $ mesons.We did not obtain reliable results for the
$ 3S $ $ s\bar{s} $ mesons and the possible vector$ s\bar{s}g $ hybrids. Therefore, we are unable to present a convincing explanation for$ \phi(2170) $ . Since the mass of$ \phi(2170) $ is compatible with the quark model prediction of the$ 3S $ $ s\bar{s} $ meson and the predicted mass of the lowest$ s\bar{s}g $ hybrids, both assignments of$ \phi(2170) $ are possible. We argue that if$ \phi(2170) $ is either the$ 3S $ $ s\bar{s} $ meson or a vector$ s\bar{s}g $ hybrid within the "color halo" picture discussed in the preceding section, the ratio$ \Gamma(\phi\eta)/\Gamma(\phi\eta') = 0.23\pm 0.10({\rm{stat}})\pm $ $0.18({\rm{syst}}) $ can be understood based on the hadronic transition of a strangeoium-like meson in addition to$ \eta-\eta' $ mixing. Nevertheless, the nature of$ \phi(2170) $ is still an open question to be investigated based on further experimental and theoretical studies.
Strangeonium-like hybrids on the lattice
- Received Date: 2020-07-30
- Available Online: 2021-01-15
Abstract: The strangeonium-like






 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF



























 DownLoad:
DownLoad: