-
The shell correction method proposed by Strutinsky [1, 2] is widely used in macroscopic-microscopic approaches for calculating the properties of atomic nuclei, such as the potential energy surface, ground-state masses and deformations, and fission barriers. At zero temperature, the ground-state masses can be calculated quickly in terms of the macroscopic-microscopic framework [3]. However, calculations of the temperature-dependent shell corrections are quite time consuming [4] owing to a large number of combinations with various shapes of the thousands of potential nuclei.
Consequently, some empirical or semi-empirical shell correction formulas have been proposed [5-12]. Based on Fermi-gas models without pairing correlation, an exponential dependence of the shell correction of the energy
$ \delta E_{\rm{shell}} $ on the excitation energy$ E^* $ , i.e.,$ \delta E_{\rm{shell}} = \delta E_{\rm{shell}} (E^* = 0) \exp(-E^*/E_d)$ is proposed in Ref. [6] and has been widely employed in many different models. The damping factor$ E_d $ varies substantially from$ 15 $ to$ 60 $ MeV [4, 13, 14]. Another functional form for a shell correction to free energy$ \delta F_{\rm{shell}} $ is suggested in Ref. [7] for closed shell nuclei, where the ratio of temperature and hyperbolic sine function$ \tau/\sinh(\tau) $ , in which$ \tau\propto T $ , is employed. In Ref. [8], a piecewise temperature dependent factor is introduced to a shell correction$ \delta E_{\rm{shell}} $ , where it stays at one until reaching the excitation energy of$ 35 $ MeV and then decreases exponentially. It was recently pointed out that both the shell corrections to energy$ \delta E_{\rm{shell}} $ and free energy$ \delta F_{\rm{shell}} $ obtained using the Woods-Saxon potential deviate from the exponential form$ \exp(-E^*/E_d) $ [12], and the shell correction$ \delta E_{\rm{shell}} $ at a temperature of$ 1 $ MeV, which corresponds to the excitation energy$ 20-30 $ MeV, is as large as that at zero temperature.For open shell nuclei, the pairing correlation cannot be ignored, and a shell correction to the pairing energy at finite temperature should be considered. Consequently, the shell corrections to the energy
$ \delta E_{\rm{shell}} $ , entropy$ T\delta S_{\rm{shell}} $ , and free energy$ \delta F_{\rm{shell}} $ are affected by the partial occupation of single particle levels [12].A reliable single-particle (s.p.) spectrum is an essential part of the Strutinsky shell correction method used for quantifying the shell effects. The covariant density functional theory (CDFT) [15-18] is a good candidate owing to its success in describing the properties of both spherical and deformed nuclei all throughout the nuclear chart, including superheavy nuclei [19-23], pseudospin symmetry [24-26], single-particle resonances [27, 28], hypernuclei [29-34], and shell correction [35-37].
The basic thermal theory was developed in a period as early as the 1950s [38]. Later, the finite temperature Hartree-Fock approximation [39-41] and the finite temperature Hartree-Fock-Bogoliubov theory [42] were developed. In 2000, B. K. Agrawal et al. investigated the temperature dependence of shapes and pairing gaps for
$ ^{166,170} $ Er and rare-earth nuclei using the relativistic Hartree-BCS theory [43, 44]. In recent years, the finite temperature relativistic Hartree-Bogoliubov theory [45] and relativistic Hartree-Fock-Bogoliubov theory [46] for spherical nuclei were developed and employed in studies in which the relations between the critical temperature for the pairing transition and pairing gap at zero temperature are explored. Following the BCS limit of the HFB theory [42], in 2017, we developed a finite-temperature covariant density functional theory for an axial-deformed space and studied the shape evolution of$ ^{72,74} $ Kr [47]. The shape evolutions of the octupole deformed nuclei$ ^{224} $ Ra and even-even$ ^{144-154} $ Ba isotopes are studied. Such nuclei first go through an octupole shape transition within the temperature range of$ 0.5-0.95 $ MeV, followed by another quadrupole shape transition from a quadrupole deformed shape to a spherical shape within a higher temperature range of$ 1.0-2.2 $ MeV [48]. Moreover, it should be noted that the transition temperatures are roughly proportional to the corresponding deformations at the ground states [49].In this paper, shell corrections to both the internal energy and the free energy are discussed based on the single-particle spectrum extracted from the axial CDFT model. This paper is organized as follows. In Section II, the finite temperature CDFT model along with the shell correction method are briefly introduced. In Section III, numerical details and checks are presented. In Section IV, the results and discussions regarding the shell corrections to the energy, free energy, and entropy, as well as their dependence on the temperature and axial deformation, are explored. Finally, a brief summary and some interesting perspectives are provided in Section V.
-
In the nuclear covariant energy density functional with a point-coupling interaction, the starting point is the following effective Lagrangian density [50],
$ \begin{aligned}[b] {\cal{L}} =& \bar\psi({\rm i}\gamma_\mu\partial^\mu-m)\psi -\frac{1}{2}\alpha_{\rm S}(\bar\psi\psi)(\bar\psi\psi) \\ & -\frac{1}{2}\alpha_{\rm V}(\bar\psi\gamma_\mu\psi)(\bar\psi\gamma^\mu\psi) -\frac{1}{2}\alpha_{\rm TV}(\bar\psi\vec\tau\gamma_\mu\psi)\cdot(\bar\psi\vec\tau\gamma^\mu\psi) \\ &-\frac{1}{3}\beta_{\rm S}(\bar\psi\psi)^3-\frac{1}{4}\gamma_{\rm S}(\bar\psi\psi)^4 -\frac{1}{4}\gamma_{\rm V}[(\bar\psi\gamma_\mu\psi)(\bar\psi\gamma^\mu\psi)]^2 \\ &-\frac{1}{2}\delta_{\rm S}\partial_\nu(\bar\psi\psi)\partial^\nu(\bar\psi\psi) -\frac{1}{2}\delta_{\rm V}\partial_\nu(\bar\psi\gamma_\mu\psi)\partial^\nu(\bar\psi\gamma^\mu\psi) \\ &-\frac{1}{2}\delta_{\rm TV}\partial_\nu(\bar\psi\vec\tau\gamma_\mu\psi)\cdot\partial^\nu(\bar\psi\vec\tau\gamma^\mu\psi)\\ &-\frac{1}{4}F^{\mu\nu}F_{\mu\nu} - e\bar\psi\gamma^\mu\frac{1-\tau_3}{2}\psi A_\mu, \end{aligned} $

(1) which is composed of a free nucleon term, four-fermion point-coupling terms, higher-order terms introduced for the effects of medium dependence, gradient terms to simulate the effects of a finite range, and electromagnetic interaction terms.
For the Lagrangian density
$ {\cal{L}} $ ,$ \psi $ is the Dirac spinor field of the nucleon with mass m,$ A_{\mu} $ and$ F_{\mu\nu} $ are respectively the four-vector potential and field strength tensor of the electromagnetic field, e is the charge unit for protons, and$ \vec{\tau} $ is an isospin vector with$ \tau_{3} $ being its third component. The subscripts S, V, and T in the coupling constants$ \alpha $ ,$ \beta $ ,$ \gamma $ , and$ \delta $ indicate the scalar, vector, and isovector couplings, respectively. The isovector-scalar (TS) channel is neglected owing to its small contributions to the description of nuclear ground state properties. In the full text, as a convention, we mark the isospin vectors with arrows and the space vectors in bold.In the framework of finite-temperature CDFT [48], the Dirac equation for a single nucleon reads
$ [\gamma_\mu({\rm i}\partial^\mu-V^\mu({{r}})) -(m+S({{r}}))]\psi_k({{r}}) = 0, $

(2) where
$ \psi_k $ is the Dirac spinor, and$\tag{3} S({{r}}) = \Sigma_{\rm S}, $

$\tag{4} V^\mu({{r}}) = \Sigma^\mu+\vec\tau\cdot\vec\Sigma^\mu_{\rm TV}, $

are respectively the scalar and vector potentials in terms of the isoscalar-scalar
$ \Sigma_{\rm S} $ , isoscalar-vector$ \Sigma^\mu $ , and isovector-vector$ \vec\Sigma^\mu_{\rm TV} $ self-energies,$\tag{5} \Sigma_{\rm S} = \alpha_{\rm S}\rho_{\rm S}+\beta_{\rm S}\rho^3_{\rm S}+\delta_{\rm S}\Delta\rho_{\rm S}, $

$\tag{6} \Sigma^\mu = \alpha_{\rm V}j^{\,\mu}_{\rm V}+\gamma_V(j^{\,\mu}_{\rm V})^3+\delta_{\rm V}\Delta j^{\,\mu}_V+eA^\mu, $

$ \tag{7} \vec\Sigma^\mu_{\rm TV} = \alpha_{\rm TV}\vec J^{\;\mu}_{\rm V}+\delta _{\rm TV}\Delta \vec J^{\;\mu}_{\rm V}. $

The isoscalar density
$ \rho_{\rm S} $ , isoscalar current$ j_{\rm V}^{\,\mu} $ , and isovector current$ \vec{j}_{\rm TV}^{\;\mu} $ are represented as follows:$\tag{8} \rho_{\rm S}({{r}}) = \sum_{k}\bar{\psi}_{k}({{r}})\psi_{k}({{r}})\left[v_{k}^{2}(1-2f_{k})+f_{k}\right], $

$\tag{9} j_{\rm V}^{\mu}({{r}}) = \sum_{k}\bar{\psi}_{k}({{r}})\gamma^{\mu}\psi_{k}({{r}})\left[v_{k}^{2}(1-2f_{k})+f_{k}\right], $

$ \tag{10} \vec{j}_{\rm TV}^{\mu}({{r}}) = \sum_{k}\bar{\psi}_{k}({{r}})\vec{\tau}\gamma^{\mu}\psi_{k}({{r}})\left[v_{k}^{2}(1-2f_{k})+f_{k}\right], $

where
$ \nu^2_k $ ($ \mu^2_k = 1-\nu^2_k $ ) is the BCS occupancy probability,$ \tag{11} \nu^2_k = \frac{1}{2}\left(1-\frac{\varepsilon_k-\lambda}{E_k}\right), $

$\tag{12} \mu^2_k = \frac{1}{2}\left(1+\frac{\varepsilon_k-\lambda}{E_k}\right), $

with
$ \lambda $ being the Fermi surface and$ E_k $ being the quasiparticle energy.At finite temperature, the occupation probability
$ \nu^2_k $ will be altered by the thermal occupation probability of quasiparticle states$ f_{k} $ , which is determined by temperature T as follows:$ f_{k} = \frac{1}{1+{\rm e}^{E_{k}/k_{\rm B}T}}, $

(7) where
$k_{\rm B}$ is the Boltzmann constant.In the BCS approach, the quasiparticle energy
$ E_k $ can be calculated as$ E_k = \sqrt{(\varepsilon_k-\lambda)^2+\Delta_k}, $

(8) where
$ \varepsilon_k $ is the single-particle energy, and the Fermi surface (chemical potential)$ \lambda $ is determined by meeting the conservation condition for particle number$ N_q $ ,$ N_q = 2\sum\limits_{k>0}\left[v_{k}^{2}(1-2f_{k})+f_k\right], $

(9) and
$ \Delta_k $ is the pairing energy gap, which satisfies the gap equation,$ \Delta_k = -\frac{1}{2}\sum\limits_{k'>0}V_{k\bar{k}k'\bar{k}'}^{pp}\frac{\Delta_{k'}}{E_{k'}}(1-2f_{k'}). $

(10) At finite temperature, the Dirac equation, mean-field potential, densities and currents, as well as the BCS gap equation in the CDFT, are solved iteratively on a harmonic oscillator basis. After a convergence is achieved, a single-particle spectrum up to
$ 30 $ MeV is extracted as an input to the following shell correction method. -
The shell corrections to the energy of a nucleus within the mean-field approximation is defined as
$ \delta E_{\rm{shell}} = E_{\rm S}-\widetilde{E}, $

(11) where
$ E_{\rm S} $ is the sum of the single-particle energy$ \varepsilon_k $ of the occupied states calculated with the exact density of states$ g_{\rm S}(\varepsilon) $ in an axially deformed space,$\tag{18} E_{\rm S} = \sum\limits_{\rm{occ.}}2\varepsilon_k = \int_{-\infty}^{\lambda}\varepsilon g_{\rm S}(\varepsilon){\rm d}\varepsilon, $

$\tag{19} g_{\rm S}(\varepsilon) = \sum\limits_k 2\delta (\varepsilon-\varepsilon_k), $

and
$ \widetilde{E} $ is the average energy calculated with the averaged density of states$ \widetilde{g}(\varepsilon) $ ,$\tag{20} \widetilde{E} = \int_{-\infty}^{\widetilde{\lambda}}\varepsilon \widetilde{g}(\varepsilon){\rm d}\varepsilon, $

$\tag{21} \widetilde{g}(\varepsilon) = \frac{1}{\gamma}\int_{-\infty}^{+\infty}f\left(\frac{\varepsilon'-\varepsilon}{\gamma}\right)g_{\rm S}(\varepsilon'){\rm d}\varepsilon', $

where
$ \widetilde{\lambda} $ is a smoothed Fermi surface,$ \gamma $ is the smoothing parameter, and$ f(x) $ is the Strutinsky smoothing function,$ f(x) = \frac{1}{\sqrt{\pi}}{\rm e}^{-x^2}L^{1/2}_M(x^2), $

(14) with
$ L^{1/2}_M(x^2) $ being the M-order generalized Laguerre polynomial.At finite temperature T, Eqs. (17)-(21) for the shell corrections can be generalized in a straightforward manner, i.e., [12],
$ \delta E_{\rm{shell}}(T) = E(T)-\widetilde{E}(T), $

(15) where for the energy
$ E(T) $ of a system of independent particles at finite temperature,$\tag{24} E(T) = \sum\limits_{\varepsilon_k}^{\lambda}2\varepsilon_k n_k^T, $

$\tag{25} n_k^T = \frac{1}{1+{\rm e}^{(\varepsilon_k-\lambda)/T}}. $

For the average energy
$ \widetilde{E}(T) $ ,$\tag{26} \widetilde{E}(T) = \int_{-\infty}^{\widetilde{\lambda}}\varepsilon \widetilde{g}(\varepsilon)n_{\varepsilon}^T{\rm d}\varepsilon, $

$\tag{27} n_{\varepsilon}^T = \frac{1}{1+{\rm e}^{(\varepsilon_k-\widetilde{\lambda})/T}}. $

The chemical potentials
$ \lambda $ and$ \widetilde{\lambda} $ are conserved by the number of neutrons (protons),$ \sum\limits_{k}2n_{k}^T = \int_{-\infty}^{\widetilde{\lambda}}{\rm d}\varepsilon\widetilde{g}(\varepsilon)n_{\varepsilon}^T = N_{q}. $

(18) The shell corrections to entropy S and free energy F at finite temperature read
$\tag{29} \delta S_{\rm{shell}}(T) = S(T)-\widetilde{S}(T), $

$\tag{30} \delta F_{\rm{shell}}(T) = F(T)-\widetilde{F}(T), $

and are related to each other as
$ \delta F_{\rm{shell}}(T) = \delta E_{\rm{shell}}(T)-T\delta S_{\rm{shell}}(T). $

(20) For the entropy
$ S_{\rm{shell}}(T) $ , the standard definition for the system of independent particles is adopted,$ S(T) = -k_{\rm B}\sum\limits_{k}2[n_k^T\ln n_k^T+(1-n_k^T)\ln (1-n_k^T)]. $

(21) The average part of
$ S(T) $ is defined in an analogous manner by replaying the sum in Eq. (32) by the integral,$ \widetilde{S}(T) = -k_{\rm B}\int_{-\infty}^{+\infty}\widetilde{g}(\varepsilon)[n_\varepsilon^T\ln n_\varepsilon^T+(1-n_\varepsilon^T)\ln (1-n_\varepsilon^T)]{\rm d}\varepsilon. $

(22) -
Taking the nucleus
$ ^{144} $ Sm with neutron shell closure as an example, the single-particle spectrum is calculated using the density functional PC-PK1 [50]. For the pairing correlation, the$ \delta $ pairing force$ V({{r}}) = V_q\delta({{r}}) $ is adopted, where the pairing strengths$ V_q $ are taken as$ -349.5 $ and$ -330.0 $ MeV$ \cdot $ fm$ ^3 $ for neutrons and protons, respectively. A smooth energy-dependent cutoff weight is introduced to simulate the effect of the finite range in the evaluation of the local pair density. Further details can be found in Ref. [48].At the mean-field level, the internal binding energies E at different axial-symmetric shapes can be obtained by applying constraints with a quadrupole deformation
$ \beta_2 $ ,$ \langle H'\rangle = \langle H\rangle +\frac{1}{2}C(\langle \hat{Q}_2\rangle-\mu_2)^2, $

(23) where C is a spring constant,
$ \mu_2 = \dfrac {3AR^2} {4\pi} \beta_2 $ is the given quadrupole moment with nuclear mass number A and radius R, and$ \langle \hat{Q}_2\rangle $ is the expectation value of quadrupole moment operator$ \hat{Q}_2 = 2r^2P_2(\cos\theta) $ .The free energy is evaluated by
$ F = E-TS $ . For convenience, the temperature used is$ k_{\rm B}T $ in units of MeV, and the entropy applied is$ S/k_{\rm B} $ , which is unitless.First, a numerical check of the binding energy convergence based on size is conducted. In Fig. 1, the average binding energy as a function of the major shell number of the harmonic oscillator basis
$ N_f $ is plotted. The binding energy is stable against the major shell number beginning from$ N_f = 16 $ and is thus fixed as a proper number. Further checks at different temperatures$ T = 0.0-2.0 $ MeV show that the temperature has a slight effect on the convergence.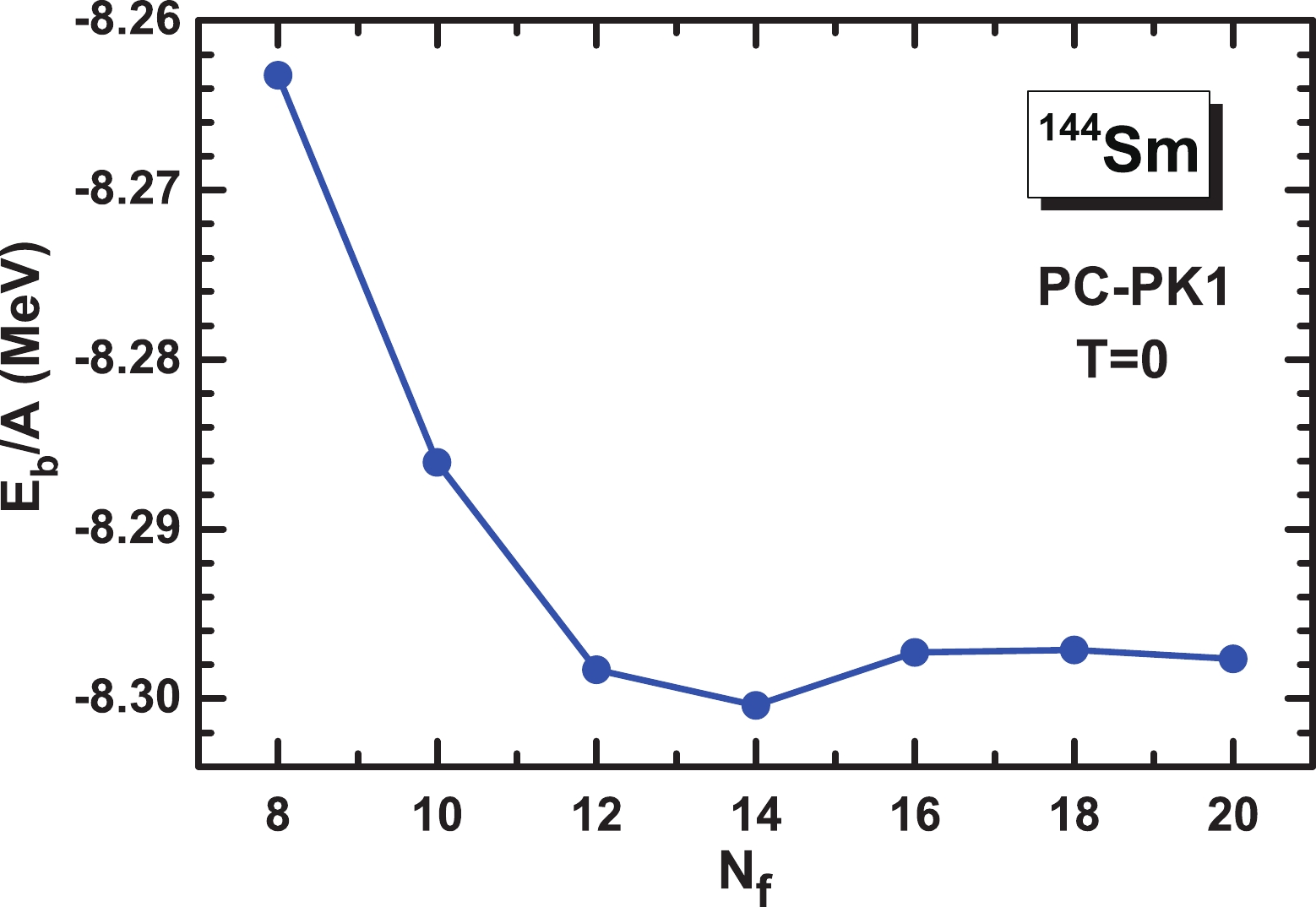
Figure 1. (color online) Average binding energy
$E_b/A$ as a function of the major shell number of the harmonic oscillator basis$N_f$ obtained by the finite temperature CDFT+BCS calculations using the PC-PK1 density functional at zero temperature.Second, the mandatory plateau condition for the shell correction method is checked. The shell correction energy should be insensitive to the smoothing parameter
$ \gamma $ and the order of the generalized Laguerre polynomial M, i.e.,$ \frac{\partial \delta E_{\rm{shell}}(T)}{\partial \gamma} = 0,\qquad\frac{\partial \delta E_{\rm{shell}}(T)}{\partial M} = 0. $

(24) In Fig. 2, the shell correction energy as a function of the above parameters
$ \gamma $ and M for$ ^{144} $ Sm is plotted. The unit of the smoothing range$ \gamma $ is$ \hbar \omega_0 = 41 A^{-1/3} (1\pm $ $\dfrac{1}{3}\dfrac{N-Z}{A}) $ MeV, where the plus (minus) sign holds for neutrons (protons). It can be seen from Fig. 2 that the optimal values are$ \gamma = 1.3 $ $ \hbar \omega_0 $ and$ M = 3 $ , which are consistent with previous relativistic calculations [35, 36].
Figure 2. (color online) Neutron shell correction energy
$\delta E_{\rm{shell}}$ as a function of the smoothing parameter$\gamma$ and the order of the generalized Laguerre polynomial M for$^{144}$ Sm obtained by the finite temperature CDFT+BCS calculations using PC-PK1 density functional at zero temperature. The four different curves correspond to the orders M = 1, 2, 3, and 4, respectively. -
The free energy curves at temperatures 0, 0.4, 0.8, 1.2, 1.6 and 2.0 MeV for
$ ^{144} $ Sm are plotted in Fig. 3. The nucleus$ ^{144} $ Sm has spherical minima for all temperatures, which are consistent with the shell closure at neutron number$ N = 82 $ . The energy curve is hard against the deformation near the spherical region. In addition, at low temperatures, a local minimum occurs at approximately$ \beta_2 = 0.7 $ and a flat minimum occurs at approximately$ \beta_2 = -0.4 $ . However, it is shown that the fine details on the potential energy curves are washed out with increases in temperatures above T = 1.2 MeV, whereas the relative structures are maintained well at low temperatures.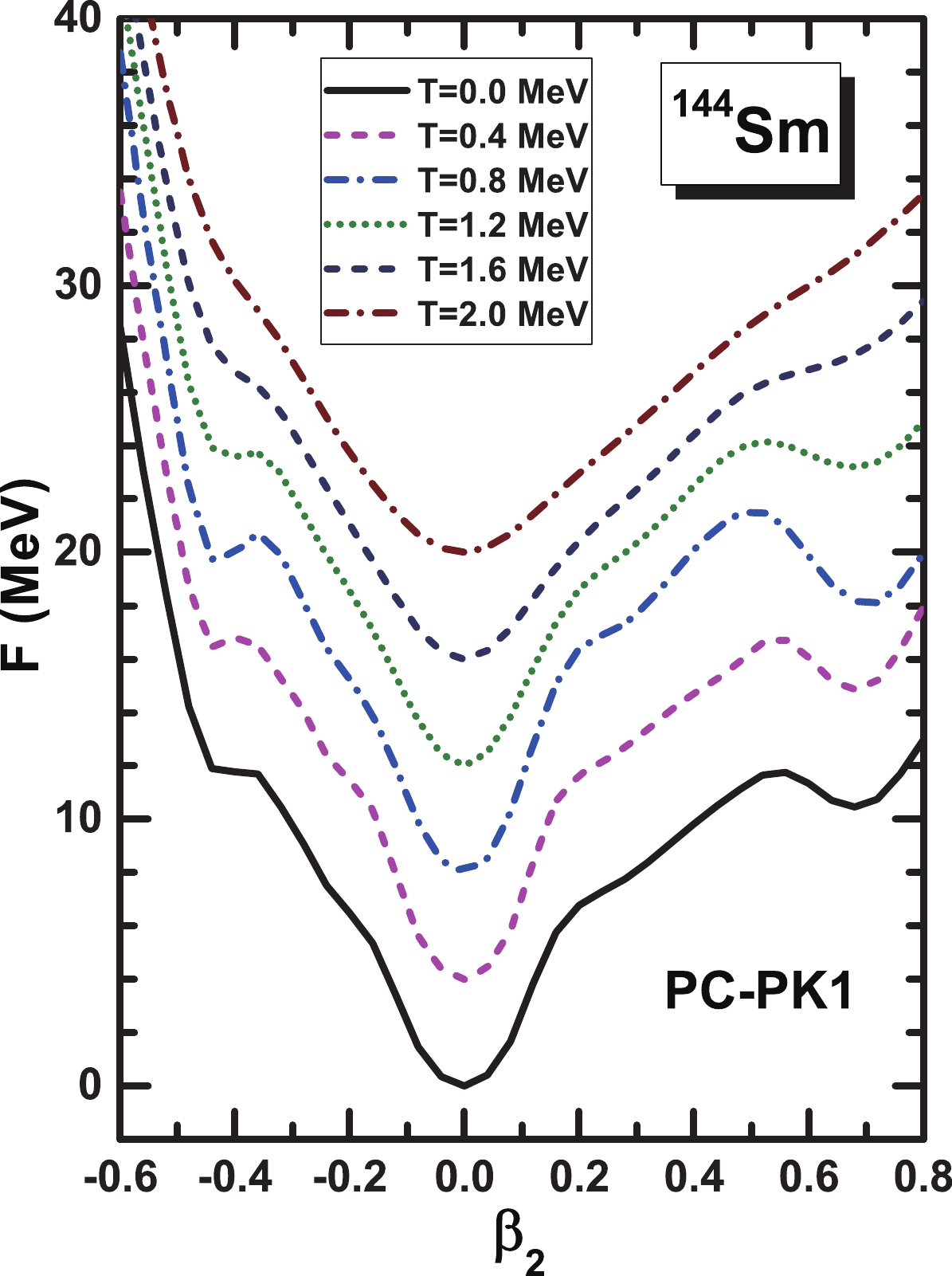
Figure 3. (color online) The relative free energy curves for
$^{144}$ Sm at different temperatures in the range of$0$ to$2$ MeV with a step of$0.4$ MeV obtained by the constrained CDFT+BCS calculations using the PC-PK1 energy density functional. The ground state free energy at zero temperature is set to zero and is shifted up by$4$ MeV for every$0.4$ MeV temperature rise.Furthermore, the shell corrections to the energy, entropy, and free energy as functions of quadrupole deformation
$ \beta_2 $ at various temperatures T are shown in Fig. 4. The shell correction to the energy$ \delta E_{\rm{shell}} $ shows a deep valley at the spherical region demonstrating a strong shell effect. In addition, the valley becomes deeper for$ T\leqslant 0.8 $ MeV and then shallower with increasing temperature, whereas the two peaks decrease dramatically after T = 0.4 MeV. The peaks and valleys on the$ \delta E_{\rm{shell}} $ curve are basically consistent with details of the free energy curve in Fig. 3. In Fig. 4(b), the entropy shell correction curve$ T \delta S_{\rm{shell}} $ changes slightly. The corresponding amplitudes are generally much smaller compared with those of$ \delta E_{\rm{shell}} $ . As the difference between$ \delta E_{\rm{shell}} $ and$ T \delta S_{\rm{shell}} $ , the curves of shell correction to the free energy$ \delta F_{\rm{shell}} $ in Fig. 4(c) have similar shapes as$ \delta E_{\rm{shell}} $ . By contrast, with increasing temperature, both the peaks and valleys of$ \delta F_{\rm{shell}} $ diminish gradually. Similar to the shell correction at zero temperature, applying a shell correction at finite temperature is a good way to quantify the shell effects, which provide rich information.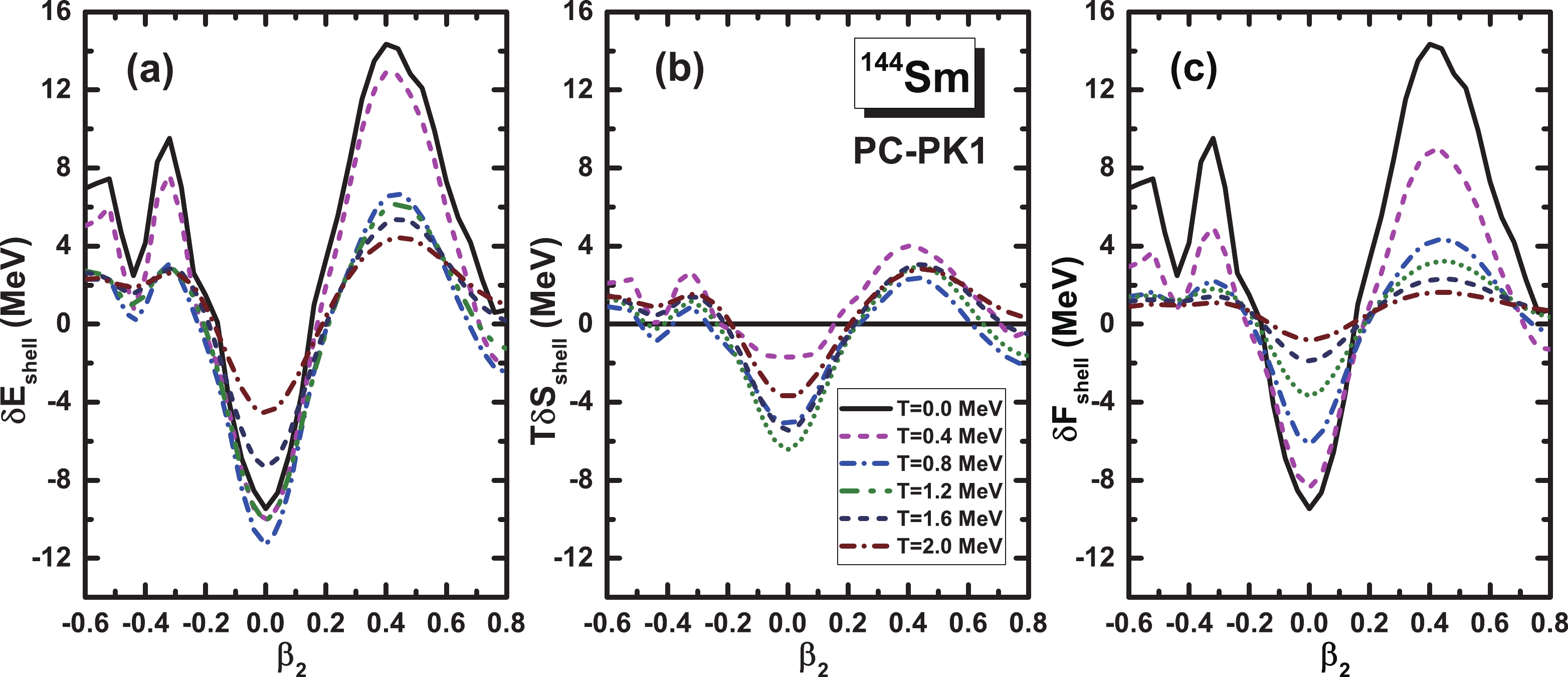
Figure 4. (color online) Neutron shell corrections to the energy
$\delta E_{\rm{shell}}$ , entropy$T\delta S_{\rm{shell}}$ , and free energy$\delta F_{\rm{shell}}$ as functions of quadrupole deformation$\beta_2$ for$^{144}$ Sm at different temperatures from$0$ to$2$ MeV with steps of$0.4$ MeV obtained by the constrained CDFT+BCS calculations using PC-PK1 energy density functional.For the minimum states of
$ ^{144} $ Sm corresponding to increases in temperatures up to 4 MeV, the shell corrections to the energy$ \delta E_{\rm{shell}} $ , entropy$ T \delta S_{\rm{shell}} $ , and free energy$ \delta E_{\rm{shell}} $ are shown in Fig. 5. The non-monotonous behavior of$ \delta E_{\rm{shell}} $ with respect to temperature is significantly different from the exponential fading. The$ \delta E_{\rm{shell}} $ first decreases and then increases, monotonously approaching zero at high temperatures. This is consistent with the Woods-Saxon potential calculations carried out in Ref. [12]. In Ref. [8], a piecewise temperature-dependent factor is multiplied by the shell correction$ \delta E_{\rm{shell}} $ . The factor remains one for low temperatures below 1.65 MeV and then decreases exponentially. Here, the absolute amplitude first enlarges to approximately 120% at a temperature of 0.8 MeV and then bounces back to approximately 90% above 1.65 MeV. For this low temperature range, such behavior is roughly consistent with that in Ref. [8]. The exponential fading holds true for high temperatures for the current case and in Refs. [8] and [12].
Figure 5. (color online) The temperature dependence of the shell corrections to the energy
$\delta E_{\rm{shell}}$ (black line), entropy$T\delta S_{\rm{shell}}$ (red line), and free energy$\delta F_{\rm{shell}}$ (blue line) with corresponding fitted empirical Bohr-Mottelson forms [7] (dashed lines) for the states with minimum free energy in$^{144}$ Sm shown in Fig. 3 obtained using the constrained CDFT+BCS calculations applying the PC-PK1 energy density functional.Because
$ \delta E_{\rm{shell}} $ is related to single-particle energy$ \varepsilon_k $ , Fermi surface$ \lambda $ , smoothed Fermi surface$ \widetilde{\lambda} $ , and temperature T according to Eqs. (23)-(27), the single particle levels near the neutron Fermi surface against the temperature for$ ^{144} $ Sm is plotted in Fig. 6. It is shown that the spectrum is almost constant within the region of$ T<0.8 $ MeV and only changes slightly at high temperature. Meanwhile, both the original Fermi surface$ \lambda $ and the smoothed surface$ \widetilde{\lambda} $ decrease synchronically with increasing temperatures. Thus, excluding$ \varepsilon_k $ ,$ \lambda $ , and$ \widetilde{\lambda} $ , the contribution directly from the temperature may play an important role in the behavior of the obtained shell correction to energy$ \delta E_{\rm{shell}} $ , as plotted in Fig. 5.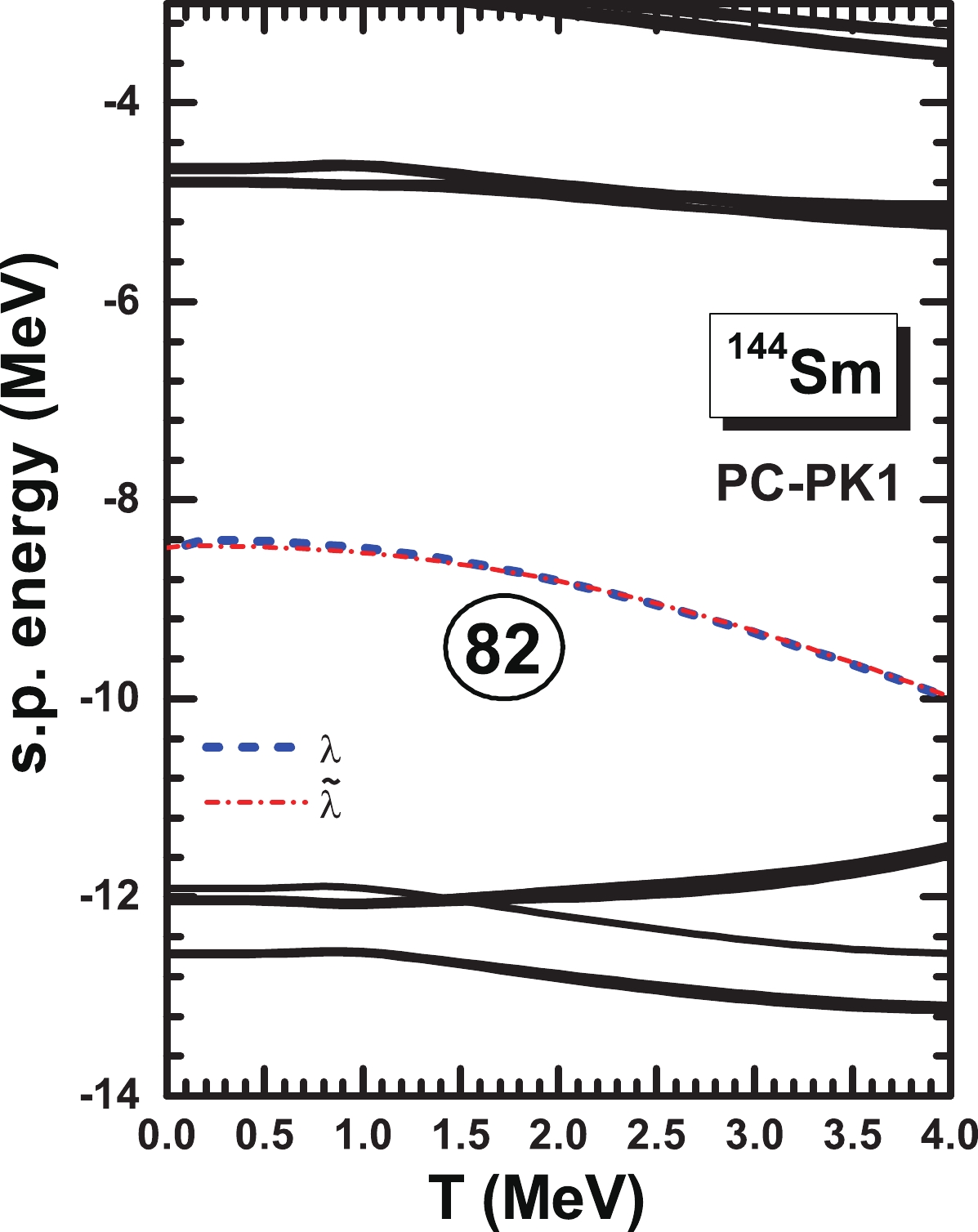
Figure 6. (color online) Neutron single-particle levels as a function of temperature for
$^{144}$ Sm obtained by the constrained CDFT+BCS calculations using PC-PK1 energy density functional. The blue dashed line and red dash-dotted line represent the original and smoothed Fermi surfaces, respectively.The shell correction to the free energy
$ \delta F_{\rm{shell}} $ increases monotonously and approaches zero at high temperatures. The shell correction to the entropy$ T\delta S_{\rm{shell}} $ behaves similar to$ \delta E_{\rm{shell}} $ . For comparison, the fitted shell corrections to free energy$ \delta F_{\rm{shell}} $ and entropy$ T\delta S_{\rm{shell}} $ in the Bohr-Mottelson form [7] are also plotted as dashed lines in Fig. 5. The Bohr-Mottelson [7] form for the shell correction to the free energy$ \delta F_{\rm{shell}} $ is expressed as$ \delta F_{\rm{shell}}(T)/\delta F_{\rm{shell}}(0) = \Psi_{\rm BM}(T) = \frac{\tau}{\sinh(\tau)}, $

(25) where
$ \tau = c_0 \cdot 2\pi^2T/\hbar\omega_0 $ with the fitting parameter$ c_0 = 2.08 $ . Similar to$ \delta F_{\rm{shell}} $ ,$ T\delta S_{\rm{shell}} $ can also be approximated as$ T\delta S_{\rm{shell}}(T) / \delta F_{\rm{shell}}(0) = \frac{T \delta S_0 [\tau \coth(\tau)-1]}{\sinh(\tau)}, $

(26) when introducing the additional parameter
$ \delta S_0 = 2.15 $ . With these two empirical formula, the shell corrections to the energy$ \delta E_{\rm{shell}} $ as the sum of$ \delta F_{\rm{shell}} $ and$ T\delta S_{\rm{shell}} $ take the following form,$ \delta E_{\rm{shell}}(T) = \delta E_{\rm{shell}}(0) \frac{\tau +T \delta S_0 [\tau \coth(\tau)-1]}{\sinh(\tau)}, $

(27) noting that
$ \delta E_{\rm{shell}}(0) $ equals$ \delta F_{\rm{shell}}(0) $ . From Fig. 5, it can be clearly seen that both the shell corrections to the free energy$ \delta F_{\rm{shell}} $ and the entropy$ T \delta S_{\rm{shell}} $ can be approximated well using the Bohr-Mottelson forms.For more evidence, the same temperature dependence of the shell correction, for both neutrons and protons, is explored in other closed-shell nuclei. In Fig. 7, the shell corrections to the energy
$ \delta E_{\rm{shell}} $ , entropy$ T\delta S_{\rm{shell}} $ , and free energy$ \delta F_{\rm{shell}} $ in$ ^{100} $ Sn and$ ^{208} $ Pb with the corresponding fitted empirical Bohr-Mottelson forms are plotted. In general, the curve shapes for all quantities are extremely similar to those of$ ^{144} $ Sm in Fig. 5, proving the same temperature dependence. In addition, the fitting parameters$ c_0 $ for the neutron and proton shell corrections to the free energy$ \delta F_{\rm{shell}} $ of$ ^{100} $ Sn and$ ^{208} $ Pb are 1.90, 2.08, 2.24, and 2.28, respectively, which are close to those of$ ^{144} $ Sm 2.08. For the neutron and proton shell corrections to the entropy$ T\delta S_{\rm{shell}} $ , the values of parameter$ \delta S_0 $ are 1.78, 2.00, 2.23, and 2.16, respectively, which are close to those of$ ^{144} $ Sm 2.15. It was demonstrated that the Bohr-Mottelson forms describe well the shell corrections for closed-shell nuclei.
Figure 7. (color online) Same as Fig. 5, but for neutrons and protons in
$^{100}$ Sn and$^{208}$ Pb. -
The temperature dependence of the shell corrections to the energy
$ \delta E_{\rm{shell}} $ , entropy$ T \delta S_{\rm{shell}} $ , and free energy$ \delta E_{\rm{shell}} $ was studied by employing the covariant density functional theory with the PC-PK1 density functional for a closed shell nucleus$ ^{144} $ Sm. For numerical checks of the harmonic oscillator basis size, the major shell number is set to$ N_f = 16 $ . The plateau condition is satisfied by$ \gamma = 1.3 $ $ \hbar \omega_0 $ and$ M = 3 $ .The fine details of the potential energy curves of free energy F are washed out with increases in temperatures above T = 1.2 MeV, whereas the relative structures are maintained well at low temperatures. Unlike the widely used exponential dependence,
$ \delta E_{\rm{shell}} $ exhibits a non-monotonous behavior. First, it decreases to a certain degree, approaching 0.8 MeV, and then dissipates exponentially, where the direct contribution from the temperature may play an important role. Such a result is consistent with the Woods-Saxon potential calculations carried out in Ref. [12]. In addition, the shell corrections to both free energy$ \delta F_{\rm{shell}} $ and entropy can be approximated well using the Bohr-Mottelson form$ \tau/\sinh(\tau) $ and$ [\tau \coth(\tau)-1]/\sinh(\tau) $ , where$ \tau\propto T $ . Further studies on shell corrections in other closed-shell nuclei,$ ^{100} $ Sn and$ ^{208} $ Pb, were conducted, and the same temperature dependencies were obtained.It was demonstrated that the shell correction at finite temperatures is a good tool for quantifying the shell effects and provides rich information. Thus, in future, open shell nuclei will also be explored, in which the shell correction to the pairing energy in the BCS framework should be explicitly considered. This is implemented in Ref. [12] with constant pairing strength G. For the
$ \delta $ -force BCS pairing, the development of the shell correction method is under way. -
The theoretical calculation was supported by the nuclear data storage system in Zhengzhou University. The authors appreciate the partial numerical work performed by ChuanXu Zhao.
Shell corrections with finite temperature covariant density functional theory
- Received Date: 2020-09-03
- Available Online: 2021-02-15
Abstract: The temperature dependence of the shell corrections to the energy





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF

























 DownLoad:
DownLoad: